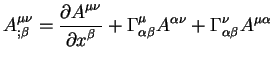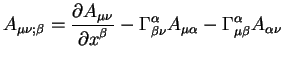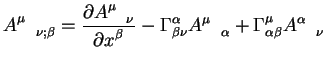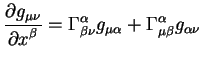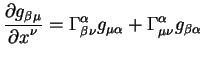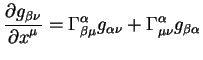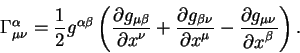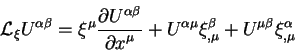Astronet > 6. Analiz v neevklidovoi geometrii

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Teoriya otnositel'nosti dlya astronomov

<< 5. Neevklidova geometriya | Oglavlenie | 7. Tenzor krivizny >>

Razdely

6. Analiz v neevklidovoi geometrii

Vychislenie razlichnyh velichin v obshei teorii otnositel'nosti - eto vychislenie tenzornyh velichin razlichnogo ranga (skalyarnyh, vektornyh, tenzornyh vtorogo ranga, inogda bolee vysokih rangov), vklyuchaya operacii differencirovaniya i integrirovaniya. V evklidovoi geometrii operaciya differencirovaniya dlya, naprimer, vektorov, opredelyalas' tak zhe kak dlya obychnyh matematicheskih funkcii - skalyarnyh velichin. V neevklidovoi geometrii procedura postroeniya proizvodnyh ot vektora yavlyaetsya bolee slozhnoi. Ona nosit nazvanie kovariantnogo differencirovaniya.

6.1 Kovariantnoe differencirovanie

Napomnim, chto esli v kazhdoi tochke nekotoroi oblasti (kotoroe mozhet ohvatyvat' i vse prostranstvo) zadana nekotoraya skalyarnaya ili vektornaya velichina, to govoryat, chto zadano pole etoi velichiny. Analogichno mozhno zadat' pole tenzornoi velichiny. Skazhem metrika Minkovskogo, opredelyaemaya kak (5.6), yavlyaetsya tenzornym polem vtorogo ranga, opredelennym vo vseh prostranstve. Kazhdaya komponenta etogo polya yavlyaetsya postoyannoi velichinoi, prichem diagonal'nye komponenty otlichny ot nulya ( $g_{00}=1$ , $g_{11}=g_{22}=g_{33}=-1$ ), a nediagonal'nye ravny nulyu. Primerom tenzornogo polya vtorogo ranga, kotoroe ne yavlyaetsya postoyannym mozhet sluzhit' metrika na poverhnosti sfery. Nediagonal'nye komponenty takoi metriki, kak i v predydushem primere, ravny nulyu, no iz diagonal'nyh komponent tol'ko komponenta $g_{11}=1$ , togda kak vtoraya komponenta yavlyaetsya funkciei odnoi iz koordinat $g_{22}=\sin^2 \theta$ .

V prostranstve s evklidovoi ili psevdoevklidovoi metrikoi v vektornom i tenzornom analize mozhno opredelit' proizvodnye ot sootvetstvuyushego polya po standartnym pravilam:

$\begin{displaymath} \frac{\partial A_{\alpha}}{\partial x^{\mu}}= \lim_{\Delta x... ...htarrow 0} \frac{\Delta A_{\alpha}(x^{\mu})}{\Delta x^{\mu}} \end{displaymath}$

(6.1)

pri $\Delta x^{\mu} \rightarrow 0$ . Zdes' neobhodimo obratit' vnimanie na to, chto v pravoi chasti stoit drob', v chislitele kotoroi nahoditsya raznost' tenzornyh velichin, vzyatyh v dvuh sosednih tochkah, $\Delta A_{\alpha} (x^{\mu})=A_{\alpha}(x^{\mu} +\Delta x^{\mu}) -A_{\alpha}(x^{\mu})$ .

V prostranstve s evklidovoi metrikoi raznost' dvuh vektorov, dazhe vzyatyh v razlichnyh tochkah prostranstva yavlyaetsya vektorom. Eta raznost' pri lineinyh preobrazovaniyah koordinat preobrazuetsya kak vektor.

Pri nelineinyh preobrazovaniyah koordinat ili v prostranstve s neevklidovoi metrikoi raznost' dvuh vektorov, vzyatyh v razlichnyh tochkah prostranstva preobrazuetsya uzhe ne po zakonu preobrazovaniya vektorov. Hotya podrobnoe izlozhenie pravil tenzornogo analiza mozhno naiti v prekrasnyh uchebnikah [8], [9], [10], my posvyatim neskol'ko abzacev demonstracii osobennostei nelineinyh preobrazovanii i preobrazovanii v neevklidovyh prostranstvah.

Vnachale pokazhem, chto pri nelineinyh preobrazovaniyah differencial vektornogo polya uzhe ne yavlyaetsya vektornym polem.

Itak, vvedem standartnoe oboznachenie:

$\begin{displaymath} \Delta A_{\mu}= A_{\mu}(x^{\alpha} +\Delta x^{\alpha}) - A_{\mu}(x^{\alpha}) \end{displaymath}$

i sdelaem preobrazovanie koordinat $\hat x^{\mu}=f^{\mu}(x^{\nu})$ , zakony preobrazovaniya dlya vektornogo polya est'

$\begin{displaymath} A_{\mu}(x^{\alpha})=\frac{\partial \hat x^{\nu}}{\partial x^{\mu}}\hat A_{\nu}\left(\hat x^{\beta}(x^{\alpha})\right) \end{displaymath}$

Pole $A_{\nu}$ v tochke $x^{\alpha} +\Delta x^{\alpha}$ budet preobrazovyvat'sya soglasno

$\begin{displaymath} A_{\mu}(x^{\alpha} +\Delta x^{\alpha})=\frac{\partial \hat ... ...u}\left(\hat x^{\beta}(x^{\alpha} +\Delta x^{\alpha})\right) \end{displaymath}$

Differencial vychislyaetsya v tochke $x^{\alpha}$ , poetomu vse funkcii neobhodimo vychislit' imenno v etoi tochke. Dlya vychisleniya chastnoi proizvodnoi v tochke $x^{\alpha}$ ispol'zuem vychisleniya vryad Teilora po malomu parametru - velichine differenciala $\Delta x^{\alpha}$ :

$\begin{displaymath} \frac{\partial \hat x^{\nu}(x^{\alpha} +\Delta x^{\alpha})}{... ...ystyle\partial x^{\mu} \partial x^{\gamma}} \Delta x^{\gamma} \end{displaymath}$

analogichnye vychisleniya prodelaem dlya samogo vektornogo polya:

$\begin{displaymath} \begin{array}{l} \hat A_{\nu}\left(\hat x^{\beta}(x^{\alpha}... ...displaystyle\partial x^{\gamma}} \Delta x^{\gamma} \end{array}\end{displaymath}$

Vse velichiny teper' vychisleny v tochke $x^{\alpha}$ , poetomu mozhem stroit' differencial i proizvodnuyu vektornogo polya po obychnym pravilam:

$\begin{displaymath} \begin{array}{l} \Delta \hat A_{\mu}= \left( {\displaystyle\... ...partial \hat x^{\beta}} \right) \Delta x^{\gamma}, \end{array}\end{displaymath}$

a proizvodnaya etogo vektornogo polya vychislyaetsya kak:

$\begin{displaymath} \begin{array}{l} {\displaystyle \partial \hat A_{\mu}\over\d... ... A_{\nu}\over\displaystyle\partial \hat x^{\beta}} \end{array}\end{displaymath}$

Vtoroi chlen v etom uravnenii obladaet priznakami tenzora, preobrazuetsya kak tenzornoe pole vtorogo ranga. Pervoe slagaemoe yavno ne yavlyaetsya tenzornym polem, poskol'ku preobrazuetsya po drugim pravilam.

Tak poluchilos' potomu, chto my prenebregli posledovatel'nymi rassuzhdeniyami v opredelenii proizvodnyh ot vektornorgo polya v neevklidovoi geometrii. Pri vychislenii prirasheniya vektornogo polya my vychitali velichiny opredelennye v raznyh tochkah prostranstva. Pervaya velichina opredelena v tochke $x^{\alpha} +\Delta x^{\alpha}$ , a vtoraya v tochke $x^{\alpha}$ . V evklidovoi geometrii pri vychislenii prirasheniya vektornogo polya obychno opuskaetsya promezhutochnyi shag, kotoryi zaklyuchaetsya v tom, chto vektory, zadannye v sosednih tochkah, svodyatsya po opredelennym pravilam v odnu tochku.

Takim pravilom yavlyaetsya parallel'nyi perenos. Differencial vektornogo polya, poluchennyi vychitaniem znacheniya vektornogo polya zadannogo v tochke $x^{\alpha}$ i parallel'no perenesennogo iz tochki $x^{\alpha}$ v tochku $x^{\alpha} +\Delta x^{\alpha}$ iz znacheniya vektornogo polya v tochke $x^{\alpha} +\Delta x^{\alpha}$ nazyvaetsya kovariantnym differencialom.

Itak, dlya polucheniya iz tenzornogo polya ranga putem differencirovaniya tenzornogo polya ranga neobhodimo vychislyat' ne obychnyi differencial, a kovariantnyi differencial.

6.1.1 Parallel'nyi perenos vektora

Kovariantnoe differencirovanie tesno svyazano s ponyatiem parallel'nogo perenosa vektora.

Parallel'nyi perenos vektora v evklidovom prostranstve opredelyaetsya kak perenos vdol' nekotoroi pryamoi takim obrazom, chto ugol mezhdu vektorom i pryamoi ostaetsya pri perenose postoyannym. Sootvetstvenno, komponenty vektora pri takom perenose ostayutsya neizmennymi.

V neevklidovoi geometrii eta operaciya neskol'ko izmenyaetsya. Analogom pryamoi v neevklidovoi geometrii yavlyaetsya geodezicheskaya liniya. Parallel'nyi perenos vektora opredelyaetsya kak perenos vdol' geodezicheskoi linii, kotoraya soedinyaet dve tochki. Estestvenno, kak i v evklidovoi geometrii, ugol mezhdu perenosimym vektorom i geodezicheskoi liniei ostaetsya postoyannym.

V kachestve harakteristiki ugla mezhdu vybrannym vektorom, skazhem, $A_{\alpha}$ i geodezicheskoi liniei prinimem ugol mezhdu vektorom $A_{\alpha}$ i vektorom kasatel'nym k geodezicheskoi linii. Takim vektorom yavlyaetsya proizvodnaya ot uravnenii geodezicheskoi linii po afinnomu parametru vdol' etoi linii $u^{\mu}={\displaystyle d x^{\mu}(\lambda)\over\displaystyle d \lambda}$ . Ugol mezhdu $A_{\alpha}$ i $u^{\alpha}$ opredelyaetsya soglasno uravneniyu (5.8). Pust' norma vektora $u^{\alpha}$ ravna edinice^6.1. Prezhde chem vesti vychisleniya, zametim, chto pri parallel'nom perenose skalyarnye velichiny ne menyayutsya^6.2. Poetomu skalyarnoe proizvedenie dvuh vektorov tozhe ostaetsya postoyannym pri parallel'nom perenose, a znachit i norma odnogo vektora postoyanna pri takom perenose. Poetomu trebovanie postoyanstva ugla mezhdu vektorom $u^{\alpha}$ i vektorom $A_{\alpha}$ mozhno zamenit' na trebovanie postoyanstva skalyarnogo proizvedeniya etih vektorov.

Itak vychislim izmenenie proizvol'nogo vektora $A_{\alpha}$ pri parallel'nom perenose vdol' geodezicheskoi linii. Osnovnoe trebonanie, nalagaemoe parallel'nym pernosom zaklyuchaetsya v tom, chto skalyarnoe proizvedenie vektora $A_{\alpha}$ i vektora kasatel'nogo k geodezicheskoi linii yavlyaetsya postoyannym vdol' linii perenosa:

$\begin{displaymath} A_{\alpha}(x^{\beta})u^{\alpha}(x^{\beta})=A_{\alpha}(x^{\beta} +\Delta x^{\beta}) u^{\alpha}(x^{\beta} +\Delta x^{\beta}) \end{displaymath}$

Vvedem oboznachenie dlya izmeneniya komponent $\delta A_{\alpha}$ vektora pri parallel'nom perenose. Teper' raspishem uravnenie sohraniya skalyarnogo proizvedeniya bolee podrobno

$\begin{displaymath} A_{\alpha} u^{\alpha} =\left(A_{\alpha} +\delta A_{\alpha}\right) \left(u^{\alpha} + d u^{\alpha}\right) \end{displaymath}$

Preobrazuem pravuyu chast' uravneniya, vydeliv chlen nulevogo poryadka malosti po beskonechno malomu smesheniyu i dva chlena pervogo poryadka malosti, vtorym poryadkom malosti zdes' budem prenebregat'. Pervyi chlen v pravoi chasti sokratitsya s chlenom, kotoryi stoit v levoi chasti, a dva chlena pervogo poryadka malosti dadut uravnenie dlya vychisleniya $\delta A_{\alpha}$ :

$\begin{displaymath} u^{\alpha}\delta A_{\alpha}= - A_{\alpha} du^{\alpha} \end{displaymath}$

Podstavim v eto uravnenie izmenenie kasatel'nogo vektora vdol' geodezicheskoi (5.13) i poluchim uravnenie dlya izmeneniya vektora $\delta A_{\alpha}$ :

$\begin{displaymath} u^{\alpha}\delta A_{\alpha}= A_{\alpha} \Gamma^{\alpha}_{\mu \nu} u^{\mu} u^{\nu} \end{displaymath}$

Otsyuda poluchaem reshenie:

$\begin{displaymath} \delta A_{\mu}= \Gamma^{\alpha}_{\mu \beta} A_{\alpha} dx^{\beta} \end{displaymath}$

V sovremennyh [10] i klassicheskih kursah [8] po obshei teorii otnositel'nosti uravnenie dlya vychisleniya izmenenii komponent vektora pri parallel'nom pernose vyvoditsya metodom perenosa vdol' pryamoi v kasatel'nom prostranstve [10] ili v galileevyh koordinatah [8]. Eti dve operacii ekvivalentny. Parallel'nyi perenos privodit k tomu, chto komponenty vektora menyayutsya.

Kovariantnyi differencial budem oboznachat' bol'shoi bukvoi latinskogo alfavita. Kovariantnyi differencial vektornogo polya $D A_{\mu}$ yavlyaetsya raznost'yu dvuh malyh velichin. Pervaya - obychnyi differencial polya $A_{\mu}$ mezhdu dvumya prostranstvenno - vremennymi tochkami $d A_{\mu}$ , vtoraya velichina - izmenenie vektornogo polya $\delta A_{\mu}$ pri parallel'nom perenose ego iz odnoi tochki prostranstva v druguyu.

$\begin{displaymath} D A_{\mu}= d A_{\mu} - \delta A_{\mu} \end{displaymath}$

Kontravariantnye komponenty $\delta A^{\mu}$ ot kovariantnyh otlichayutsya znakom:

$\begin{displaymath} \delta A^{\mu}= -\Gamma^{\mu}_{\alpha \beta} A^{\alpha} dx^{\beta} \end{displaymath}$

Teper' mozhno napisat' uravneniya dlya kovariantnyh differencialov

$\begin{displaymath} \begin{array}{l} D A^{\mu}= \left( {\displaystyle\partial A^... ...^{\alpha}_{\mu \beta} A_{\alpha} \right)dx^{\beta}, \end{array}\end{displaymath}$

a takzhe uravneniya dlya kovariantnyh proizvodnyh ot vektorov

$\begin{displaymath} \begin{array}{l} A^{\mu}_{;\beta}= {\displaystyle\partial A... ...{\beta}} -\Gamma^{\alpha}_{\mu \beta} A_{\alpha} \end{array} \end{displaymath}$

Znak ";" oznachaet kovariantnuyu proizvodnuyu. My budem v dal'neishem ispol'zovat' etot znak "tochka s zapyatoi" dlya oboznacheniya kovariantnoi proizvodnoi, a dlya oboznacheniya obychnoi proizvodnoi budem ispol'zovat' znak "," - "zapyataya".

Legko videt', chto kovariantnyi differencial podchinyaetsya vsem osnovnym pravilam differencirovaniya:

$\displaystyle D (C \cdot A_{\mu}) =C D A_{\mu}$
$\displaystyle D (A_{\mu} \pm B_{\mu}) =D A_{\mu} \pm D B_{\mu}$
$\displaystyle D (A_{\mu} \cdot B_{\nu}) =B_{\nu} \cdot D A_{\mu} +A_{\mu} \cdot D B_{\nu}$			(6.2)
$\displaystyle D (A_{\mu} \cdot B^{\nu}) =B^{\nu} \cdot D A_{\mu} +A_{\mu} \cdot D B^{\nu},$

pol'zuyas' etimi pravilami mozhno dokazat' pravilo obrazovaniya kovariantnyh proizvodnyh ot tenzorov bolee vysokogo ranga chem vektora:

$\displaystyle A^{\mu \nu}_{;\beta}= {\displaystyle\partial A^{\mu \nu}\over\dis... ...{\mu}_{\alpha \beta} A^{\alpha \nu} +\Gamma^{\nu}_{\alpha \beta} A^{\mu \alpha}$			(6.3)
$\displaystyle \qquad{}$			(6.4)
$\displaystyle A_{\mu \nu; \beta}= {\displaystyle\partial A_{\mu \nu}\over\displ... ...^{\alpha}_{\beta \nu} A_{\mu \alpha}-\Gamma^{\alpha}_{\mu \beta} A_{\alpha \nu}$			(6.5)
$\displaystyle \qquad{}$			(6.6)
$\displaystyle A^{\mu}_{\quad \nu; \beta}= {\displaystyle\partial A^{\mu}_{\quad... ...\nu} A^{\mu}_{\quad \alpha} +\Gamma^{\mu}_{\alpha \beta} A^{\alpha}_{\quad \nu}$			(6.7)

Obratim vnimanie, chto v sluchae smeshannyh indeksov poryadok mozhet byt' vazhen, v tom sluchae, kogda tenzor ne yavlyaetsya simmetrichnym. Togda ukazanie na to, chto indeks dolzhen sledovat' vtorym pokazano otstupom, verhnii i nizhnii indeksy ne raspolozheny v odnoi kolonke. To zhe samoe spravedlivo i dlya simvolom Kristoffelya.

Teper' mozhno prosto sformulirovat' slovesnoe pravilo obrazovaniya kovari antnoi proizvodnoi ot tenzora lyubogo ranga i soderzhashego proizvol'noe kolichestvo nizhnih i verhnih indeksov. Kovariantnaya proizvodnaya ravnyaetsya summe chastnoi proizvodnoi ot tenzora po nekotoroi koordinate plyus (ili minus) proizvedeniya simvolov Kristoffelya na sam tenzor. Kolichestvo chlenov v etoi summe ravnyaetsya kolichestvu indeksov plyus chastnaya proizvodnaya ot samogo tenzora. Bolee tochno, kovariantnaya proizvodnaya ot tenzora ranga , soderzhashego verhnih i nizhnih indeksov ravnyaetsya chastnoi proizvodnoi ot etogo tenzora, plyus proizvedenie simvola Kristoffelya (s verhnim indeksom takim zhe kak odin iz verhnih indeksov differenciruemogo tenzora i odnim iz nizhnih indeksov takih zhe kak u koordinaty, po kotoroi vedetsya differencirovanie) s samim tenzorom u kotorogo odin iz verhnih indeksov summiruetsya so vtorym indeksom simvola Kristoffelya, minus proizvedenie simvola Kristofferya (teper' verhnii indeks u svyaznosti yavlyaetsya nemym indeksom summirovaniya, a odin iz nizhnih indeksov takoi zhe kak u koordinaty po kotoroi vedetsya differencirovanie) s samim tenzorom u kotorogo ocherednyi nizhnii indeks zamenen na nem oi indeks summirovaniya, a ostal'nye raspolozheny po poryadku.

Kovarintnye proizvodnye podchinyayutsya tem zhe obychnym pravilam differencirovaniya, kotorye spravedlivy dlya obychnyh proizvodnyh ot vektornyh i tenzornyh polei v evklidovam prostranstve. Eti pravila perechisleny chut' vyshe dlya variacii vektora (sm. uravnenie (6.2)).

Dobavim, chto kovariantnaya proizvodnaya ot skalyarnogo polya sovpadaet s obychnoi proizvodnoi.

Zakony preobrazovanii simvolov Kristoffelya pri preobrazovaniyah koordinat imeyut vid:

$\begin{displaymath} \Gamma^{\alpha}_{\mu \nu}={\displaystyle\partial x^{\alpha}\... ...le\partial x^{\alpha}\over\displaystyle\partial \hat x^{\rho}} \end{displaymath}$

V obychnoi neevklidovoi geometrii predpologaetsya, chto simvol Kristoffelya yavlyaetsya simmetrichnym po nizhnim indeksam.

Sushestvuet obobsheniya neevklidovoi geometrii v kotoroi simvol Kristoffelya uzhe ne yavlyaetsya simmetrichnym. Raznost'

$\begin{displaymath} S^{\alpha}_{\mu \nu} = \Gamma^{\alpha}_{\mu \nu} - \Gamma^{\alpha}_{\nu \mu} \end{displaymath}$

nazyvaetsya tenzorom krucheniya. V otlichie ot simvola Kristoffelya, kotoryi ne yavlyaetsya tenzorom i preobrazuetsya po zakonu, soderzhashemu vtoruyu proizvodnuyu ot koordinat, velichina $S^{\alpha}_{\mu \nu}$ yavlyaetsya tenzorom i, kak legko proverit', preobrazuetsya kak tenzor tret'ego ranga.

V obshei teorii otnositel'nosti tenzor krucheniya raven nulyu, eksperimenty pokazyvayut, chto vvedenie etoi velichiny izlishne. Poetomu dalee my ne budem rassmatrivat' tenzor krivizny i ego nablyudatel'nye proyavleniya. V obshei teorii otnositel'nosti simvol Kristoffelya yavlyaetsya simmetrichnym po nizhnim indeksam, chto vyrazhaetsya uravneniem vida $\Gamma^{\alpha}_{\mu \nu}=\Gamma^{\alpha}_{\nu \mu}$ . Vsyudu nizhe budem polagat', chto $\Gamma^{\alpha}_{\mu \nu}$ yavlyaetsya simmetrichnym po indeksam ${ \bf\mu \nu}$ .

6.2 Svyaz' metricheskogo tenzora i simvolov Kristoffelya

Dlya vychisleniya kovariantnyh proizvodnyh v neevklidovoi geometrii neobhodimo nauchit'sya vychislyat' simvoly Kristoffelya. Oni vychislyayutsya ochen' prosto v metricheskih prostranstvah, kogda $\Gamma^{\alpha}_{\mu \nu}$ opredelyaetsya cherez metricheskii tenzor. Naidem svyaz' $\Gamma^{\alpha}_{\mu \nu}$ s metricheskim tenzorom.

Kovariantnyi differencial yavlyaetsya tenzorom, poetomu soglasno pravilu podnyatiya i opuskaniya indeksov v metricheskih prostranstvah mozhno napisat' uravnenie:

$\begin{displaymath} D A_{\mu}= g_{\mu \nu} D A^{\nu} \end{displaymath}$

(6.8)

s drugoi storony analogichnoe uravnenie mozhno napisat' dlya samih vektorov

$\begin{displaymath} A_{\mu}= g_{\mu \nu} A^{\nu} \end{displaymath}$

(6.9)

Teper' prodifferencirum (6.9) i primenim pravila (6.2). Poluchim uravnenie vida

$\begin{displaymath} D A_{\mu}= g_{\mu \nu} D A^{\nu} + A^{\nu} D g_{\mu \nu} \end{displaymath}$

(6.10)

Iz sravnenii uravnenii (6.8) i (6.10) vidno, chto kovariantnyi differencial ot metricheskogo tenzora raven nulyu. Sledovatel'no ravny nulyu kovariantnye proizvodnye po vsem koordinatam. Vychislim kovariantnye proizvodnye v yavnom vide soglasno uravneniyu (6.5). Eti kovariantnye proizvodnye imeyut vid:

$\begin{displaymath} g_{\mu \nu; \beta}= {\displaystyle\partial g_{\mu \nu}\over\... ...u} g_{\mu \alpha }-\Gamma^{\alpha}_{\mu \beta} g_{\alpha \nu} \end{displaymath}$

(6.11)

Poskol'ku levaya chast' uravneniya (6.11) ravna nulyu, kak eto sleduet iz uravneniya (6.10), to i pravaya tozhe ravna nulyu. V rezul'tate poluchaem lineinoe uravnenie dlya svyazi simvolov Kristoffelya s metricheskim tenzorom i ego chastnymi proizvodnymi pervogo poryadka:

$\begin{displaymath} {\displaystyle\partial g_{\mu \nu}\over\displaystyle\partial... ...g_{\mu \alpha }-\Gamma^{\alpha}_{\mu \beta} g_{\alpha \nu} =0 \end{displaymath}$

(6.12)

Perestavlyaya indeksy v uravnenii (6.12) poluchaem sistemu lineinyh uravnenii vida:

$\displaystyle {\displaystyle\partial g_{\mu \nu}\over\displaystyle\partial x^{\... ...\alpha}_{\beta \nu} g_{\mu \alpha } +\Gamma^{\alpha}_{\mu \beta} g_{\alpha \nu}$			(6.13)
$\displaystyle {\displaystyle\partial g_{\beta \mu}\over\displaystyle\partial x^... ...\alpha}_{\beta \nu} g_{\mu \alpha } +\Gamma^{\alpha}_{\mu \nu} g_{\beta \alpha}$			(6.14)
$\displaystyle {\displaystyle\partial g_{\beta \nu}\over\displaystyle\partial x^... ...{\alpha}_{\beta \mu} g_{\alpha \nu} +\Gamma^{\alpha}_{\mu \nu} g_{\beta \alpha}$			(6.15)

Vychitaya pochlenno iz uravneniya (6.13) uravneniya (6.14) i (6.15), poluchaem uravnenie

$\begin{displaymath} 2g_{\beta \alpha} \Gamma^{\alpha}_{\mu \nu}= {\displaystyle\... ...yle\partial g_{\mu \nu}\over\displaystyle\partial x^{\beta}} , \end{displaymath}$

iz kotorogo legko nahodim svyaz' simvolov Kristoffelya s metricheskim tenzorom i ego pervymi proizvodnymi po koordinatam:

$\begin{displaymath} \Gamma^{\alpha}_{\mu \nu}= {\displaystyle 1\over\displaystyl... ...tial g_{\mu \nu}\over\displaystyle\partial x^{\beta}}\right). \end{displaymath}$

(6.16)

Kak vidno iz uravneniya (5.11) eti dva simvola sovpadayut.

6.2.1 Kovariantnaya proizvodnaya 4^x skorosti

Rassmotrim teper' kovariantnuyu proizvodnuyu odnogo iz samyh vazhnyh dlya nas vektorov - 4 skorosti probnoi chasticy ili vektora kasatel'nogo k geodezicheskoi linii. Kovariantnyi differencial etogo vektora est':

$\begin{displaymath} D u^{\alpha} = d u^{\alpha} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} d x^{\nu} \end{displaymath}$

Teper' mozhno vychislit' chastnuyu kovariantnuyu proizvodnuyu po odnoi iz koordinat:

$\begin{displaymath} u^{\alpha}_{; \nu} = {\displaystyle\partial u^{\alpha}\over\... ...aystyle\partial x^{\nu}} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} \end{displaymath}$

v sootvetstvii s obshimi pravilami kovariantnogo differencirovaniya. Umnozhim eto uravnenie na sam vektor 4 skorosti:

$\begin{displaymath} u^{\alpha}_{; \nu} u^{\nu} = {\displaystyle\partial u^{\alph... ...x^{\nu}} u^{\nu} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} u^{\nu} \end{displaymath}$

Pervyi chlen v pravoi chasti etogo uravneniya, kak legko videt', raven polnoi proizvodnoi ot skorosti po afinnomu parametru vdol' geodezicheskoi linii:

$\begin{displaymath} {\displaystyle\partial u^{\alpha}\over\displaystyle\partial ... ... u^{\nu} = {\displaystyle d u^{\alpha}\over\displaystyle d s} \end{displaymath}$

Oba chlena vmeste predstavlyayut uravnenie geodezicheskoi linii, otkuda imeem eshe odin vid uravneniya geodezicheskoi:

$\begin{displaymath} u^{\alpha}_{\quad ; \mu} \; u^{\mu} =0 \end{displaymath}$

(6.17)

6.3 Proizvodnaya Lagranzha -Eilera

V matematicheskom analize i geometrii ispol'zuyut eshe neskol'ko vidov proizvodnyh. Dlya nas vazhnymi yavlyayutsya dve iz nih, eto proizvodnaya Lagranzha -Eilera i proizvodnaya Li. Vnachale poznakomimsya s proizvodnoi Lagranzha -Eilera.

Rassmotrim mnozhestvo funkcii $\Phi_{A}(x^{\alpha})$ koordinat $x^{\alpha}$ . Eti funkcii mogut byt' komponentami skalyara, vektora ili tenzora. Oni mogut byt' ob'ektami drugoi prirody, kotorye preobrazuyutsya k drugoi sisteme koordinat po sobstvennym pravilam. Dlya vychisleniya proizvodnoi Lagranzha -Eilera nevazhna priroda etih funkcii. My opustim indeks , no budem pomnit', chto funkcii $\Phi$ predstavlyayut iz sebya nabor funkcii.

Rassmotrim funkciyu $\bf L$ ot argumentov, kotorye sami yavlyayutsya funkciyami i ih proizvodnymi:

$\begin{displaymath} {\bf L}(\Phi, \Phi_{, \mu}, \Phi_{, \mu, \nu}, \Phi_{, \mu, \nu, \xi}, \mbox{ i tak dalee}) \end{displaymath}$

Eshe raz podcherknem, chto $\Phi$ v obshem sluchae yavlyaetsya mnozhestvom funkcii, a ne obyazatel'no odnoi funkciei.

Rassmotrim teper' funkcional, naprimer deistvie ot funkcii ${\bf L}$ :

$\begin{displaymath} S = \int {\bf L} d^4 x \end{displaymath}$

vzyatoe po nekotoroi 4 oblasti $\Omega$ .

Oboznachim $\delta \Phi$ variaciyu polya $\Phi$ i budem schitat', chto variacii samogo polya, a takzhe vseh ego proizvodnyh ischezayut na granice oblasti $\Omega$ .

Variacii funkcii ${\bf L}$ imeyut vid:

$\begin{displaymath} \delta {\bf L}={\displaystyle\partial {\bf L}\over\displayst... ...i_{, \mu, \nu}} \delta \Phi_{, \mu, \nu} + \mbox{i tak dalee} \end{displaymath}$

Otsyuda poluchaem dlya variacii funkcionala uravnenie vida:

$\begin{displaymath} \delta \int {\bf L} d^4 x = \int \left( {\displaystyle\parti... ...} \delta \Phi_{, \mu, \nu} + \mbox{i tak dalee} \right) d^4 x \end{displaymath}$

Integriruya kazhdyi iz chlenov v kruglyh skobkah po chastyam poluchaem:

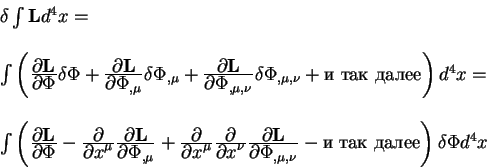
$\begin{displaymath} \begin{array}{l} \delta \int {\bf L} d^4 x = \\ \qquad \\ ... ...} - \mbox{i tak dalee} \right) \delta \Phi d^4 x \end{array} \end{displaymath}$

Vyrazhenie, kotoroe nahoditsya v kruglyh skobkah v poslednei strochke nazyvaetsya proizvodnoi Lagranzha -Eilera. Itak po opredeleniyu velichina:

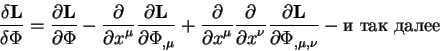
$\begin{displaymath} {\displaystyle\delta {\bf L}\over\displaystyle\delta \Phi} =... ...\displaystyle\partial \Phi_{, \mu, \nu}} - \mbox{i tak dalee} \end{displaymath}$

nazyvaetsya proizvodnoi Lagranzha -Eilera ot L. Ona tesno svyazana c funkcional'noi ili variacionnoi proizvodnoi vvodimoi v teorii sluchainyh polei [11].

Uravnenie vida:

$\begin{displaymath} {\displaystyle\delta {\bf L}\over\displaystyle\delta \Phi} = 0 \end{displaymath}$

nazyvaetsya uravneniem Eilera. Uravneniya takogo vida yavlyayutsya uravneniyami dvizheniya v n'yutonovskoi mehanike. Inogda v kachestve velichiny $\Phi$ vystupaet peremennaya, kotoraya voobshe ne preobrazuetsya.

6.4 Proizvodnaya Li

Proizvodnaya Li dlya nas ne tak vazhna, kak proizvodnaya Lagranzha - Eilera, no vse zhe my kratko proanaliziruem ee zdes', poskol'ku budem obrashat'sya k nei neskol'ko raz v techenie kursa. Bolee podrobno o metode Li i ego primeneniyah budet rasskazano nizhe.

Proizvodnaya Li igraet bol'shoe znachenie pri issledovanii svoistv simmetrii metriki. Dlya issledovaniya etih svoistv napomnim vnachale prosteishee ponyatie simmetrii, naprimer zerkal'noi simmetrii. Geometricheskoe telo nazyvayut simmetrichnym otnositel'no ploskosti, esli eta ploskost' razbivaet telo na dve chasti, iz kotoryh kazhdaya yavlyaetsya zerkal'nym otrazheniem drugoi otnositel'no etoi ploskosti. Sama ploskost' v etom sluchae nazyvaetsya ploskost'yu simmetrii. Zerkal'noi simmetriei obladayut mnogie predmety iz okruzhayushego nas mira: samolet, list klena, forma chelovecheskogo tela (vnutrennee stroenie uzhe ne obladaet svoistvom zerkal'noi simmetrii!).

S formal'noi tochki zreniya zerkal'nuyu simmetriyu opredelyayut kak forminvariantnost' otnositel'no preobrazovaniya koordinat vida:

$\begin{displaymath} x \rightarrow -x \hskip0.3cm . \end{displaymath}$

Esli pri takom preobrazovanii koordinat forma tela ostaetsya neizmennoi, to govoryat, chto geometricheskoe telo simmetrichno otnositel'no ploskosti

Otmetim, chto privedennoe vyshe preobrazovanie ne yavlyaetsya nepreryvnym otnositel'no nekotorogo parametra, kak v bol'shinstve sluchaev, kotorye my rassmatrivali pri preobrazovaniyah koordinat v neevklidovoi geometrii. Poetomu svoistva simmetrii geometricheskih tel, tochnee funkcii svyazany s invariantnost'yu pri preobrazovaniyah koordinat. Zerkal'naya simmetriya otnosit'sya k tak nazyvaemym diskretnym vidam simmetrii.

Nizhe my budem rassmatrivat' tol'ko tochechnye vidy simmetrii. Oni svyazany s nepreryvnymi preobrazovaniyami, nepreryvno zavisyat ot odnogo ili neskol'kih parametrov. K takim vidam simmetrii otnositsya, naprimer, simmetriya otnositel'no vrasheniya. Tak, sfera - ideal'nyi ob'ekt v trehmernom prostranstve dlya izucheniya gruppy vrashenii. Vrasheniya mozhno osushestvlyat' na proizvol'nyi, skol' ugodno malyi, ugol.

Opredelim ponyatie simmetrii dlya metricheskogo tenzora. Govoryat, chto metrika $g_{\mu \nu}$ yavlyaetsya forminvariantnoi otnositel'no preobrazovanii koordinat vida $\tilde x^{\mu}=f^{\mu}(x^{\alpha})$ , esli preobrazovannaya metrika $\tilde g_{\mu \nu}(\tilde x^{\alpha})$ - ta zhe funkciya ot argumenta $\tilde x^{\mu}$ , chto i pervonachal'naya funkciya $g_{\mu \nu}( x^{\alpha})$ ot ee pervonachal'nogo argumenta $x^{\alpha}$ , t.e. [12]

$\begin{displaymath} \tilde g_{\mu \nu}(\tilde x^{\alpha}) = g_{\mu \nu}( x^{\alpha}) \hskip1cm \mbox{dlya vseh } x^{\alpha} \end{displaymath}$

Zametim, chto eto ravenstvo mozhno takzhe perepisat' v dvuh ekvivalentnyh formulirovkah:

$\begin{displaymath} \tilde g_{\mu \nu}( x^{\alpha}) = g_{\mu \nu}( x^{\alpha}) \hskip1cm \mbox{dlya vseh } x^{\alpha} \end{displaymath}$

$\begin{displaymath} \tilde g_{\mu \nu}(\tilde x^{\alpha}) = g_{\mu \nu}(\tilde x^{\alpha}) \hskip1cm \mbox{dlya vseh } \tilde x^{\alpha} \end{displaymath}$

Mnogie geometricheskie svoistva prostranstva mozhno opredelit' pol'zuyas' ponyatiyami simmetrii. Simmetrii prostranstva takzhe vazhny dlya opredeleniya fizicheskih svoistv, zakonov sohraneniya, poiska naibolee obshih integralov uravnenii dvizheniya. Svoistva metriki prostranstva - vremeni mozhno opredelit' ne pribegaya k resheniyu uravnenii obshei teorii otnositel'nosti, a pol'zuyas' tol'ko soobrazheniyami simmetrii. Poyasnim kak eto mozhno sdelat' na primere proizvodnyh Li.

Proizvodnye Li yavlyayutsya obosheniyami ponyatiya proizvodnyh po napravleniyu na tenzory. Rassmotrim dve tochki v prostranstve i , razdelennye malym rasstoyaniem. Pust' koordinaty etih tochek soedinyayutsya beskonechno malym vektorom, kvadratom kotorogo mozhno prenebrech' po sravneniyu s samim vektorom^6.3:

$\begin{displaymath} x^{\mu}(P_1) = x^{\mu}(P_0) + \xi^{\mu} \end{displaymath}$

Pust' zadano nekotoroe skalyarnoe pole $\Phi(x^{\alpha})$ . Vychislim znachenie polya $\Phi$ v tochke esli znachenie etogo polya v tochke zadano:

$\begin{displaymath} \Phi(P_1) = \Phi(P_0) + \xi^{\mu} {\displaystyle\partial \Phi\over\displaystyle\partial x^{\mu}} \end{displaymath}$

Estestvenno, v etom razlozhenii $\Phi(P_1)$ v ryad Teilora mozhno prenebrech' kvadratichnymi popravkami i popravkami bolee vysokih stepenei. Velichina:

$\begin{displaymath} {\cal L}_{\xi} \Phi = \xi^{\mu} {\displaystyle\partial \Phi\over\displaystyle\partial x^{\mu}} \end{displaymath}$

(6.18)

nazyvaetsya proizvodnoi Li ot skalyarnogo polya. V kursah vysshei matematiki etot operator chashe nazyvaetsya proizvodnoi po napravleniyu $\xi^{\mu}$ .

Rassmotrim smysl takoi proizvodnoi na primere skalyarnogo polya, zadannogo v trehmernom prostranstve. Pust' u nas zadano cilindricheski - simmetrichnoe raspredelenie temperatury v prostranstve s cilindricheskimi koordinatami , i $\varphi$ . Intuitivno ponyatno, chto temperatura mozhet zaviset' ot radiusa , no ona ne budet zaviset' ot koordinaty ili ot koordinaty $\varphi$ . Eto oznachaet, chto proizvodnaya ot temperatury po koordinatam , $\varphi$ ravna nulyu. V invariantnom vide eto oznachaet, chto sushestvuyut vektora, vydelyayushie napravlenie vdol' kotoryh proizvodnaya Li ravna nulyu. V dannom chastnom sluchae eto vektora opisyvayushie dvizheniya vdol' osi i vokrug nee. V obshem sluchae dvizhenie, kotoroe opisyvaet vektor $\xi^{\mu}$ , opisyvaet tochechnuyu simmetriyu, esli znachenie polya $\Phi$ v dvuh tochkah i vdol' etogo vektora yavlyaetsya postoyannym.

Teper' opredelim proizvodnuyu Li dlya vektornogo polya $A^{\mu}(x^{\nu})$ . Ot sluchaya skalyarnogo polya eta proizvodnaya otlichaetsya tem, chto teper' vychislyaetsya velichina, kotoraya zavisit ot koordinatnoi sistemy. Itak, vnov' u nas est' dve tochki, kotorye razdeleny beskonechno malym vektorom $\xi^{\mu}$ . Znacheniya vektornogo polya v tochke cherez znacheniya v tochke vychislyayutsya kak:

$\begin{displaymath} A^{\mu}(P_1) = A^{\mu}(P_0) + \xi^{\alpha} {\displaystyle\partial A^{\mu}\over\displaystyle\partial x^{\alpha}} \end{displaymath}$

Rassmotrim teper' preobrazovanie koordinat:

$\begin{displaymath} \tilde x^{\alpha} = x^{\alpha} + \xi^{\alpha} (x), \end{displaymath}$

gde $\xi^{\alpha}$ - tot zhe samyi vektor beskonechno maloi velichiny. Teper', kak netrudno videt', tochka imeet te zhe znacheniya koordinat v til'dovannoi sisteme, chto i tochka v netil'dovannoi sisteme. Koefficenty v matrice preobrazovaniya vektorov dlya takogo preobrazovaniya imeyut vid:

$\begin{displaymath} {\displaystyle\partial \tilde x^{\alpha}\over\displaystyle\p... ...partial \xi^{\alpha}(x)\over\displaystyle\partial x^{\beta}} \end{displaymath}$

Sootvetstvenno koefficenty v matrice preobrazovaniya vektora v tochke est':

$\begin{displaymath} \tilde A^{\mu}(P_1) = {\displaystyle\partial \tilde x^{\mu}\over\displaystyle\partial x^{\nu}} A^{\nu}(P_1) \end{displaymath}$

ili

$\begin{displaymath} \tilde A^{\mu}(P_1) = \left( \delta^{\mu}_{\nu} + \xi^{\mu},_{\nu}\right) A^{\nu}(P_1) \end{displaymath}$

Zapishem teper' znachenie vektora v tochke cherez znachenie v tochke , togda poluchim:

$\begin{displaymath} \tilde A^{\mu}(P_1) = A^{\mu}(P_0) + \xi^{\alpha} {\displays... ...playstyle\partial x^{\alpha}} + \xi^{\mu},_{\nu} A^{\nu}(P_0) \end{displaymath}$

Raznica mezhdu preobrazovannymi komponentami vektornogo polya v tochke i nepreobrazovannymi komponentami vektornogo polya v tochke nazyvaetsya differencialom Li ili proizvodnoi Li:

$\begin{displaymath} {\cal L}_{\xi} A^{\mu} = \xi^{\alpha} {\displaystyle\partial... ...r\displaystyle\partial x^{\alpha}} + \xi^{\mu},_{\nu} A^{\nu} \end{displaymath}$

(6.19)

Analogichno mozhno opredelit' proizvodnuyu Li dlya tenzornogo polya. Rassmotrim teper' kakoe - libo tenzornoe pole, naprimer, obrazovannoe iz tenzora vtorogo ranga, kotoroe v sisteme koordinat bez til'dy imeet komponenty $U^{\alpha \beta} (x)$ . V preobrazovannoi sisteme koordinat ono imeet vid:

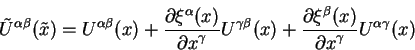
$\begin{displaymath} \tilde U^{\alpha \beta} (\tilde x) = U^{\alpha \beta} ( x) ... ...)\over\displaystyle\partial x^{\gamma}} U^{\alpha \gamma} (x) \end{displaymath}$

Tak otlichayutsya komponenty tenzora ${\bf U}$ v til'dovannoi i netil'dovannoi sistemah koordinat. Teper' vychislim komponenty etogo tenzora v tochkah i .

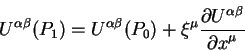
$\begin{displaymath} U^{\alpha \beta}(P_1) = U^{\alpha \beta}(P_0) + \xi^{\mu}{\d... ...\partial U^{\alpha \beta}\over\displaystyle\partial x^{\mu}} \end{displaymath}$

Okonchatel'no vychislim raznicu mezhdu znacheniyami komponent tenzora v tochke v netil'dovannoi sisteme koordinat i znacheniyami komponent tenzora v tochke v til'dovannoi sisteme koordinat. Eta velichina nazyvaetsya proizvodnoi Li dlya tenzorov vtorogo ranga:

$\begin{displaymath} {\cal L}_{\xi} U^{\alpha \beta} = \xi^{\mu}{\displaystyle\pa... ...pha \mu} \xi^{\beta}_{,\mu} +U^{\mu \beta} \xi^{\alpha}_{,\mu} \end{displaymath}$

(6.20)

Teper' mozhno opredelit' simmetriyu tenzornogo polya ${\bf U}$ otnositel'no vektornogo polya $\xi^{\mu}$ kak ravenstvo nulyu proizvodnoi Li (6.20).

Vernemsya teper' k simmetriyam metricheskogo tenzora. Proizvodnaya Li metricheskogo tenzora vyglyadit osobenno prosto:

$\begin{displaymath} {\cal L}_{\xi} g_{\mu \nu} =- \xi_{\mu ; \nu} - \xi_{\nu ; \mu} \end{displaymath}$

(6.21)

Eto prosto proveryaetsya neposredstvennym vychisleniem. Ravenstvo nulyu proizvodnoi Li daet nam uravnenie Killinga:

$\begin{displaymath} \xi_{\mu ; \nu} + \xi_{\nu ; \mu} = 0 , \end{displaymath}$

(6.22)

kotoroe opredelyaet simmetrii metricheskogo tenzora.

<< 5. Neevklidova geometriya | Oglavlenie | 7. Tenzor krivizny >>

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe: 70 let Stivenu Hokingu Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vsemirnyi god fiziki: triumf Einshteina Al'bert Einshtein opisyvaet prostranstvo-vremya Polnoe solnechnoe zatmenie Otdel pul'sarnoi astrometrii PRAO AKC FIAN O skorosti gravitacii - ot avtorov Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce