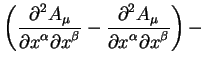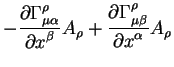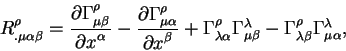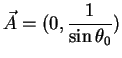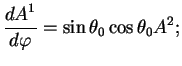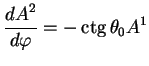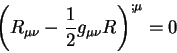Astronet > 7. Tenzor krivizny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Teoriya otnositel'nosti dlya astronomov

<< 6. Analiz v neevklidovoi | Oglavlenie | 8. Uravnenie dvizheniya v >>

Razdely

7. Tenzor krivizny

Neevklidova geometriya polnost'yu harakterizuetsya metricheskim tenzorom. Odnako pomimo etogo tenzora sushestvuet eshe neskol'ko vazhnyh tenzorov, kotorye tozhe ispol'zuyutsya dlya harakteristiki vazhnyh sootnoshenii neevklidovoi geometrii. Samoi vazhnoi velichinoi posle metricheskogo tenzora yavlyaetsya tenzor krivizny ili, kak dlya kratkosti govoryat relyativisty, krivizna. Tenzor krivizny mozhno vvodit' neskol'kimi putyami. My obsudim zdes' dva sposoba opredeleniya tenzora krivizny. Pervyi sposob - cherez vtorye kovariantnye proizvodnye ot vektora, vtoroi sposob bolee tradicionnyi - posredstvom sravneniya kovariantnogo perenosa vektora po dvum putyam, obrazuyushim zamknutuyu krivuyu.

7.1 Tenzor krivizny

7.1.1 Vtorye kovariantnye proizvodnye

Pust' v nashem prostranstve zadano vektornoe pole $A_{\mu}(x^{\alpha})$ . Rassmotrim pervye proizvodnye etogo vektornogo polya i vtorye proizvodnye polya $A_{\mu}(x^{\alpha})$ . Poskol'ku bol'shinstvo uravnenii matematicheskoi fiziki - uravneniya soderzhashie vtorye proizvodnye ot fizicheskoi velichiny, to pri obobshenii uravnenii opisyvayushih kakoe - libo pole, naprimer, elektromagnitnoe, nam pridetsya vyvodit' uravneniya, kotorye soderzhat vtorye proizvodnye ot polei po koordinatam. V evklidovoi geometrii poryadok proizvodnyh byl nevazhen, proizvodnye obladali svoistvom kommutacii. V neevklidovoi geometrii eto svoistvo, voobshe govorya, teryaetsya.

Rassmotrim kovariantnye proizvodnye vtorogo poryadka. Takuyu proizvodnuyu mozhno zapisat' kak

$\begin{displaymath} A_{\mu; \alpha; \beta} ={\displaystyle\partial A_{\mu; \alph... ..._{\rho; \alpha} - \Gamma^{\rho}_{\alpha \beta} A_{\mu; \rho}, \end{displaymath}$

(7.1)

tak kak $A_{\mu; \alpha}$ yavlyaetsya tenzorom vtorogo ranga. Teper' podstavim uravnenie dlya pervoi kovariantnoi proizvodnoi v (7.1) i poluchim uravnenie vida:

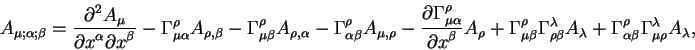
$\begin{displaymath} A_{\mu; \alpha; \beta} ={\displaystyle\partial^2 A_{\mu}\ove... ...rho}_{\alpha \beta} \Gamma^{\lambda}_{\mu \rho} A_{\lambda} , \end{displaymath}$

v etoi formule, kak i prezhde, tochka s zapyatoi pered indeksom oznachayut kovariantnoe differencirovanie po koordinate imenuemoi etim indeksom, zapyataya - chastnuyu proizvodnuyu po koordinate s odnoimennym indeksom.

Teper' vypishem raznost' kovariantnyh proizvodnyh menyaya indeksy po kotorym vedetsya differencirovanie.

$\displaystyle A_{\mu; \alpha; \beta} -A_{\mu; \beta; \alpha} =$			(7.2)
$\displaystyle \qquad$
$\displaystyle \left({\displaystyle\partial^2 A_{\mu}\over\displaystyle\partial ... ...ial^2 A_{\mu}\over\displaystyle\partial x^{\alpha} \partial x^{\beta}}\right) -$
$\displaystyle \qquad$
$\displaystyle - \Gamma^{\rho}_{\mu \alpha} A_{\rho, \beta} - \Gamma^{\rho}_{\mu... ...ho}_{\mu \alpha} A_{\rho, \beta} + \Gamma^{\rho}_{\beta \alpha} A_{\mu, \rho} -$
$\displaystyle \qquad$
$\displaystyle - {\displaystyle\partial \Gamma^{\rho}_{\mu \alpha}\over\displays... ...artial \Gamma^{\rho}_{\mu \beta}\over\displaystyle\partial x^{\alpha}} A_{\rho}$
$\displaystyle \qquad$
$\displaystyle + \Gamma^{\rho}_{\mu \beta} \Gamma^{\lambda}_{\rho \beta} A_{\lam... ...mbda} - \Gamma^{\rho}_{\beta \alpha } \Gamma^{\lambda}_{\mu \rho} A_{\lambda} ,$

Proanaliziruem poluchennoe uravnenie. Prezhde vsego obratim vnimanie, chto v levoi chasti uravneniya pervaya strochka, kotoraya soderzhit antikommutator ot chastnym proizvodnyh obrashaetsya v nol'. Takim obrazom antikommutator kovariantnyh proizvodnyh ponizhaet poryadok differencirovaniya. Vtoraya strochka soderzhit pervye chastnye proizvodnye ot vektornogo polya. Zametim, chto pervyi i pyatyi chleny vzaimno sokrashayutsya, takzhe sokrashayutsya poocheredno vtoroi i chetvertyi, a takzhe tretii i shestoi chleny. Takim obrazom antikommutator kovariantnyh proizvodnyh vtorogo poryadka ne soderzhit chastnyh proizvodnyh voobshe. Odnako, uravnenie (7.2) ne obrashaetsya v nol' tozhdestvenno.

Tret'ya strochka poluchennogo uravneniya, kotoraya soderzhit proizvedeniya chastnyh proizvodnyh ot simvola Kristoffelya na vektornoe pole ne obrashetsya v nol' tozhdestvenno. V poslednei strochke vzaimno sokrashayutsya vtoroi i chetvertyi chleny, no pervyi i tretii chleny ne sokrashayutsya. Takim obrazom, poluchaetsya, chto antikommutator kovariantnyh proizvodnyh vtorogo poryadka raven proizvedeniyu samogo vektornogo polya na velichinu soderzhashuyu chetyre indeksa:

$\begin{displaymath} A_{\mu; \alpha; \beta} -A_{\mu; \beta; \alpha} = \\ \qquad \\ R^{\rho}_{. \mu \alpha \beta} A_{\rho} \end{displaymath}$

(7.3)

Teper' legko dokazat', chto velichina $R^{\rho}_{. \mu \alpha \beta}$ yavlyaetsya tenzorom. Deistvitel'no, sdelaem preobrazovanie koordinat iz odnoi sistemy (skazhem, $\lbrace x^{\mu}\rbrace$ ) v druguyu $\lbrace \hat x^{\mu}\rbrace$ . Sleva v uravnenii (7.3) stoit tenzornaya velichina tret'ego ranga (napomnim, chto pervaya kovariantnaya proizvodnaya ot vektora yavlyaetsya tenzorom vtorogo ranga, sootvetstvenno vtoraya kovariantnaya proizvodnaya ot vektora yavlyaetsya tenzorom tret'ego ranga). Sprava v etom uravnenii - proizvedenie vektora na velichinu s chetyr'mya indeksami. Sravnivaya zavisimost' v dvuh sistemah koordinat poluchaem zakon preobrazovaniya dlya $R^{\rho}_{. \mu \alpha \beta}$ v vide:

$\begin{displaymath} \hat R^{\rho}_{. \mu \alpha \beta} = {\displaystyle\partial... ...e\partial \hat x^{\beta}} R^{\varrho}_{. \lambda \zeta \eta} \end{displaymath}$

Eto dokazyvaet, chto velichina $R^{\rho}_{. \mu \alpha \beta}$ yavlyaetsya tenzorom chetvertogo ranga.

Etot tenzor nazyvaetsya tenzorom krivizny ili tenzorom Rimana^7.1. Ego mozhno zapisat' v vide uravneniya v chastnyh proizvodnyh simvolov Kristoffelya i binarnyh proizvedenii simvolov.

$\begin{displaymath} R^{\rho}_{. \mu \alpha \beta} = {\displaystyle\partial \Gamm... ... \Gamma^{\rho}_{\lambda \beta} \Gamma^{\lambda}_{\mu \alpha}, \end{displaymath}$

(7.4)

Zdes' znaki v opredelenii tenzora krivizny vybrany tak, chtoby tenzor sovpadal s opredeleniem prinyatym v [8]. Nekotorye avtory opredelyayut tenzor Rimana s protivopolozhnym znakom.

7.2 Parallel'nyi perenos vektora po zamknutoi krivoi

V etoi chasti my rassmotrim vtoroi, tradicionnyi vyvod tenzora krivizny. V klassicheskih knigah, posvyashennyh neevklidovoi geometrii i obshei teorii otnositel'nosti, tenzor krivizny poyavlyaetsya pri obsuzhdenii parallel'nogo perenosa vektora po zamknutoi krivoi (sm. naprimer, [8], [10]).

Itak, rassmotrim parallel'nyi perenos vektora vdol' zamknutoi krivoi. Dlya poyasneniya vykladok vnachale vyberem dvumernuyu poverhnost' sfery, a v kachestve vektora edinichnyi vektor kasatel'nyi k traektorii perenosa v nachal'noi tochke. Krivuyu narisuem na poverhnosti sfery i budem schitat', chto eta krivaya - parallel' ili liniya shiroty.

7.2.1 Parallel'nyi perenos vektora po linii shiroty na sfere

Metriku v koordinatah $\theta, \varphi$ mozhno zapisat' kak (5.9):

$\begin{displaymath} ds^2=d\theta^2 +\sin^2\theta d\varphi^2, \end{displaymath}$

a metricheskii tenzor budet imet' vid

$\begin{displaymath} g_{\alpha \beta}= \left( \begin{array}{cc} 1& 0 \\ 0& \sin^2 \theta\\ \end{array} \right) \end{displaymath}$

Krome togo, vypishem vnov' takzhe komponenty simvola Kristoffelya na poverhnosti edinichnoi sfery:

$\begin{displaymath} \Gamma^1_{22}=- \sin \theta \cos \theta \qquad \Gamma^2_{12}= \ctg \theta \end{displaymath}$

Vektor perenositsya vdol' shiroty na sfere parallel'no. Eto znachit, chto kovariantnaya proizvodnaya etogo vektora vdol' vybrannoi krivoi ravna nulyu. Poetomu formal'no uslovie parallel'nogo pernosa zapisyvaetsya kak:

$\begin{displaymath} D A^{a} =0. \end{displaymath}$

Teper' napishem eto formal'noe uslovie bolee detal'no:

$\begin{displaymath} d A^{a} = \Gamma^{a}_{m n} A^{m} d x^{n} \end{displaymath}$

(7.5)

Pust' na paralleli, kotoraya harakterizuetsya odnim parametrom - koordinatoi $\theta=\theta_0$ , zadan vektor edinichnoi dliny:

$\displaystyle \vec A =(0, {\displaystyle 1\over\displaystyle\sin \theta_0})$			(7.6)
$\displaystyle (\vec A \vec A) = (A^1)^2 + \sin^2 \theta_0 (A^2)^2 =1$			(7.7)

Vektor perenositsya vdol' shiroty, a eto znachit, chto izmenenie koordinaty $\theta$ otsutstvuet, $d \theta =0$ . Uravneniya (7.5) prinimayut vid:

$\displaystyle d A^1 = \sin \theta_0 \cos \theta_0 A^2 d \varphi$			(7.8)
$\displaystyle d A^2 = -\ctg \theta_0 A^1 d \varphi$			(7.9)

Vnachale rassmotrim vspomogatel'nyi primer. Sdvinem vektor vdol' shiroty na rasstoyanie $\Delta \varphi$ . Ego komponenty izmenyatsya. Poyavitsya komponenta napravlennaya vdol' pervoi osi:

$\begin{displaymath} \Delta A^1={1 \over 2}\sin 2\theta_0 \Delta \varphi, \end{displaymath}$

a komponenta vdol' vtoroi osi ostanetsya neizmennoi (s tochnost'yu do malyh velichin vtorogo poryadka):

$\begin{displaymath} A^2(\varphi +\Delta \varphi) = {1 \over \sin \theta_0} \end{displaymath}$

Teper' vidno, chto vektor povernulsya ( poskol'ku poyavilas' komponenta vdol' pervoi osi). Ugol mezhdu parallel'no perenesennym vektorom i vektorom, kasatel'nym k shirote est':

$\begin{displaymath} \cos \psi =\cos \theta_0 \Delta \varphi. \end{displaymath}$

Rassmotrim teper' matematicheskie operacii bolee podrobno i reshim uravneniya parallel'nogo perenosa vektora dlya vychisleniya ego komponent posle pereneseniya na konechnoe rasstoyanie vdol' shiroty. Uravneniya (7.8) stanovyatsya:

$\displaystyle {\displaystyle d A^1\over\displaystyle d \varphi} = \sin \theta_0 \cos \theta_0 A^2;$			(7.10)
$\displaystyle {\displaystyle d A^2\over\displaystyle d \varphi} = - \ctg \theta_0 A^1$			(7.11)

Teper' uravneniya opisyvayushie parallel'nyi perenos vektora - eto dva obyknovennyh differencial'nyh uravneniya. Prodifferenciruem vtoroe iz uravnenii (7.10) po peremennoi $\varphi$ i podstavim ego v pervoe. Poluchim odno uravnenie vtorogo poryadka:

$\begin{displaymath} {\displaystyle d^2 A^2\over\displaystyle d \varphi^2} = - \cos^2 \theta_0 A^2. \end{displaymath}$

Ego reshenie - eto reshenie uravneniya kolebanii, kogda chastota kolebanii ravna $\cos \theta_0$ . Eto reshenie imeet vid:

$\begin{displaymath} A^2 (\varphi) = A_0 \cos (\varphi \cos \theta_0) + A_1 \sin( \varphi \cos \theta_0) \end{displaymath}$

Estestvenno, chto reshenie zavisit ot dvuh postoyannyh velichin i .

Sootvetstvenno reshenie dlya pervoi komponenty vektora poluchaetsya differencirovaniem po $\varphi$ i umnozheniem na $- \tg \theta_0$ :

$\begin{displaymath} A^1 (\varphi) = A_0 \sin \theta_0 \sin (\varphi \cos \theta_0) - A_1 \sin \theta_0 \cos( \varphi \cos \theta_0) \end{displaymath}$

Naidem teper' postoyannye i . V tochke $\varphi =0$ komponenty vektora est' , $A^2={\displaystyle 1\over\displaystyle\sin \theta_0}$ . Podstavim eti usloviya v naidennye resheniya dlya komponent i poluchim, chto $A_0={\displaystyle 1\over\displaystyle\sin \theta_0}$ , a . Poetomu resheniya dlya komponent vektora imeyut vid:

$\begin{displaymath} \begin{array}{l} A^1(\varphi) = \sin( \varphi \cos \theta_0)... ...rphi \cos \theta_0)\over\displaystyle\sin \theta_0} \end{array}\end{displaymath}$

Naidem ugol mezhdu vektorom $\vec A$ i edinichnym vektorom, kasatel'nym k linii shiroty $\vec u =(0, {\displaystyle 1\over\displaystyle\sin \theta_0})$ . Etot ugol budet opredelyat'sya uravneniem:

$\begin{displaymath} \cos \psi = {\displaystyle(\vec A(\varphi) \vec u)\over\disp... ...rt^2}\sqrt{\vert\vec u\vert^2}} = \cos (\varphi \cos \theta_0) \end{displaymath}$

Proekciya vektora $\vec A$ na vektor $\vec u$ umen'shaetsya po mere perenosa $\vec A$ vdol' shiroty. V to zhe vremya proekciya vektora $\vec A$ na edinichnyi vektor vdol' meridiana, nazovem ego $\vec v =(1, 0)$ rastet:

$\begin{displaymath} \cos \iota = {\displaystyle(\vec A(\varphi) \vec v)\over\dis... ...rt^2}\sqrt{\vert\vec v\vert^2}} = \sin (\varphi \cos \theta_0) \end{displaymath}$

Vektor, kasatel'nyi k linii meridiana napravlen ot polyusa. Posmotrim na sferu so storony severnogo polyusa. Pust' perenos osushestvlyaetsya v napravlenii protiv chasovoi strelki. Togda povorot vektora $\vec A$ proishodit po chasovoi strelke.

Rassmotrim bolee podrobno perenos vektora po shirote raspolozhennoi blizko k polyusu. Budem schitat', chto $\theta_0 \approx 0$ , i budem prenebregat' chlenami kvadratichnymi po shirote. Togda $A^1 \approx \sin(\varphi), \; \; A^2 \approx {\displaystyle\cos(\varphi)\over\displaystyle\theta_0}$ . Rassmotrim znacheniya komponent v tochke $\varphi={\displaystyle\pi\over\displaystyle 2}$ . Pri etom vidno, chto komponenta, napravlennaya vdol' $\vec u$ obrashaetsya v nol', a komponenta, napravlennaya vdol' vektora $\vec v$ stanovit'sya pochti edinichnoi. Pri perenose vdol' shiroty znachitel'no otstoyashei ot polyusa, komponenta $\vec A$ vdol' $\vec u$ obrashaetsya v nol' pri znachenii ugla $\varphi ={\displaystyle\pi\over\displaystyle 2 \cos \theta_0}$ .

Pri dal'neishem perenose ugol mezhdu $\vec A$ i $\vec u$ prodolzhaet rasti. Posle polnogo perenosa vektora $\vec A$ i vozvrasheniya ego v tochku $\varphi =0$ ugol mezhdu perenesennym vektorom i vektorom $\vec u$ est':

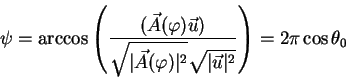
$\begin{displaymath} \psi =\arccos\left( {\displaystyle(\vec A(\varphi) \vec u)\o... ...\vert^2}\sqrt{\vert\vec u\vert^2}}\right) = 2\pi \cos \theta_0 \end{displaymath}$

Otmetim takzhe, chto ugol mezhdu ishodnym polozheniem vektora i ego konechnym polozheniem est'

$\begin{displaymath} 2\pi (1 - \cos \theta_0), \end{displaymath}$

chto v tochnosti ravno ploshadi segmenta sfery edinichnogo radiusa, ogranichennogo liniei shiroty.

Esli vektor perenositsya parallel'no samomu sebe na ploskosti vdol' zamknutoi krivoi, to posle vozvrasheniya v ishodnuyu tochku, vektor sovpadaet sam s soboi. V neevklidovoi geometrii eto ne tak. Sledovatel'no geometriya na sfere neekvivalentna geometrii na ploskosti. Chut' nizhe my uvidim, chto vyvedennye uravneniya imeyut otnoshenie k krivizne poverhnosti.

Rassmotrim teper' parallel'noe perenesenie vektora vdol' zamknutoi krivoi v proizvol'noi neevklidovoi geometrii.

7.2.2 Perenos vektora po beskonechno malomu parallelogrammu

Prezhde chem issledovat' povedenie vektora $\vec A$ pri parallel'nom pernose vdol' zamknutoi krivoi proizvol'noi formy, my rassmotrim perenos etogo vektora vdol' beskonechno malogo parallelogramma postroennogo na otrezkah sootvetstvuyushih koordinat.

Risunok 7.1: Na risunke izobrazhen beskonechno malyi parallelogramm. Vershiny parallelogramma oboznacheny bukvami

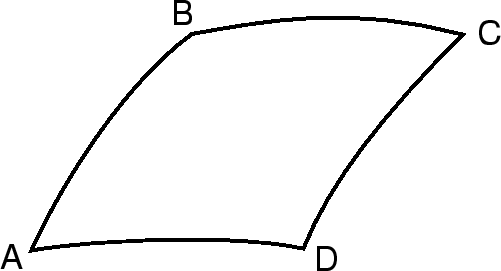$\begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig7_1.ai}}\end{figure}$

Itak, pust' u nas zadan vektor $A^{\alpha}$ . Vershiny parallelogramma oboznachim (sm. ris. 7.1). Tochku i tochku soedinyaet beskonechno malyi vektor $d x^{\mu}_2$ . Tochku i tochku soedinyaet beskonechno malyi vektor $d x^{\mu}_1$ . Poskol'ku nasha figura - parallelogramm, to storony, protivopolozhnye storonam i soedinyayut vektora poluchennye parallel'nym perenosom. Storona, kotoraya postroena na vektore soedinyayushem tochki i , protivopolozhna storone postroennoi na vektore $d x^{\mu}_1$ . Etot vektor, parallel'no perenesennyi na $d x^{\mu}_2$ , est' $d x^{\mu}_1 - \Gamma^{\mu}_{\alpha \beta} d x^{\alpha}_1 d x^{\beta}_2$ . Storona, kotoraya postroena na vektore, soedinyayushem tochki i , protivopolozhna storone, postroennoi na vektore $d x^{\mu}_2$ . Etot vektor, parallel'no perenesennyi na $d x^{\mu}_1$ , est' $d x^{\mu}_2 - \Gamma^{\mu}_{\alpha \beta} d x^{\alpha}_2 d x^{\beta}_1$ . Takim obrazom my vychislili razmer storon parallelogramma.

Vychislim teper' izmenenie komponent vektora pri perenesenii. Pust' vektor $A^{\alpha}$ zadannyi v tochke perenositsya parallel'no samomu sebe vnachale cherez tochku v tochku , a zatem iz tochki cherez tochku v tochku .

Rassmotrim vnachale perenos iz v cherez tochku . Velichina vektora, perenesennogo v est':

$\begin{displaymath} A^{\alpha} - \Gamma^{\alpha}_{\mu \nu} A^{\mu} d x^{\nu}_2 \end{displaymath}$

Teper' etot vektor dolzhen byt' perenesen iz tochki v tochku . No v tochke znacheniya simvolov Kristoffelya uzhe drugie:

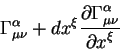
$\begin{displaymath} \Gamma^{\alpha}_{\mu \nu} +dx^{\xi} {\displaystyle\partial \Gamma^{\alpha}_{\mu \nu}\over\displaystyle\partial x^{\xi}} \end{displaymath}$

Posle pereneseniya iz tochki v vektor vnov' izmenyaetsya. Sledovatel'no vektor, perenesennyi iz v cherez imeet vid:

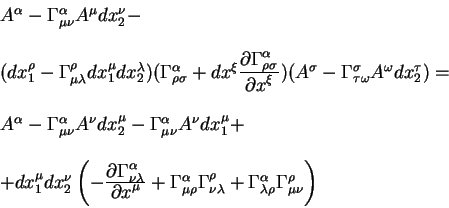
$\begin{displaymath} \begin{array}{l} A^{\alpha} - \Gamma^{\alpha}_{\mu \nu} A^{\... ...a}_{\lambda \rho} \Gamma^{\rho}_{\mu \nu }\right) \end{array} \end{displaymath}$

Zdes' my prenebregli velichinami tret'ego poryadka malosti.

Dlya vektora perenesennogo iz v cherez tochku poluchaem analogichnoe vyrazhenie, v kotorom vektora $d x^{\mu}_1$ i $d x^{\mu}_2$ menyayutsya mestami. Teper' mozhno vychislit' raznost' mezhdu dvumya vektorami, perenesennymi v po dvum traektoriyam. Eta raznost' ravna:

$\begin{displaymath} d x^{\mu}_1 d x^{\nu}_2 \lbrace {\displaystyle\partial \Gamm... ...ha}_{\mu \rho} \Gamma^{\rho}_{\nu \lambda}\rbrace A^{\lambda} \end{displaymath}$

(7.12)

Eto vyrazhenie yavlyaetsya vektorom, tak kak postroena kak algebraicheskaya summa vektorov. Drugimi slovami, vyrazhenie, kotoroe stoit v figurnyh skobkah, yavlyaetsya tenzorom chetvertogo ranga. Etot tenzor:

$\begin{displaymath} R^{\alpha}_{\mu \nu \lambda} = {\displaystyle\partial \Gamma... ...mbda} -\Gamma^{\alpha}_{\mu \rho} \Gamma^{\rho}_{\nu \lambda} \end{displaymath}$

(7.13)

nazyvaetsya tenzorom krivizny. Poetomu prostranstvo yavlyaetsya evklidovym, esli (7.13) raven nulyu v kazhdoi tochke etogo prostranstva.

Proizvedenie dvuh vektorov na kotoryh postroen parallelogramm est' ploshad' etogo beskonechno malogo parallelogramma.

7.2.3 Izmenenie vektora pri perenose po zamknutoi krivoi

Rassmotrim teper' izmenenie vektora pri parallel'nom perenose vdol' zamknutoi krivoi konechnogo razmera. Razob'em ee na beskonechno malye parallelogrammy, kak pokazano na ris. 7.2

Risunok 7.2: Na risunke izobrazhena zamknutaya krivaya konechnyh razmerov

. Razob'em ee na sovokupnost' beskonechno malyh parallelogrammov tak, chtoby perenos po sosednim storonam parallelogrammov prohodil v protivopolozhnyh napravleniyah. Togda, kak legko videt', polnoe izmenenie vektora pri perenose vdol'

skladyvaetsya iz integrala po ploshadi, styagivaemoi etoi krivoi ot proizvedeniya tenzora krivizny na sam vektor.

$\begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig7_2.ai}}\end{figure}$

Teper' mozhno poluchit' izmenenie komponent vektora $A^{\alpha}$ pri parallel'nom pernose vdol' zamknutoi krivoi konechnyh razmerov v vide integrala po poverhnosti, styagivaemoi etoi krivoi:

$\begin{displaymath} \Delta A^{\alpha} = -{1 \over 2} \int dS^{\mu \nu} R^{\alpha}_{\beta \mu \nu } A^{\beta} \end{displaymath}$

7.3 Svoistva tenzora krivizny

Svoistva tenzora krivizny my uzhe nemnogo obsudili pri analize vtoroi kovariantnoi proizvodnoi ot vektora. Obsudim algebraicheskie svoistva tenzora krivizny bolee podrobno. Dlya etogo opustim verhnii indeks i budem rabotat' tol'ko s kovariantnym tenzorom chetvertogo ranga.

Iz uravneniya (7.4) sleduyut svoistva simmetrii tenzora krivizny:

$\displaystyle R_{\alpha \beta \mu \nu}= -R_{\beta \alpha \mu \nu}$			(7.14)
$\displaystyle R_{\alpha \beta \mu \nu}= -R_{\alpha \beta \nu \mu}$			(7.15)
$\displaystyle R_{\alpha \beta \mu \nu}= R_{\mu \nu \alpha \beta }$			(7.16)
$\displaystyle R_{\alpha \beta \mu \nu} + R_{\alpha \nu \beta \mu} +R_{\alpha \mu \nu \beta } =0$			(7.17)

Do sih por my rassmatrivali obshii sluchai neevklidovoi geometrii, teper' vspomnim, chto nam nuzheno tol'ko chetyrehmernoe prostranstvo. V etom sluchae pary indeksov $\alpha \beta$ i $\mu \nu$ probegayut 6 razlichnyh naborov znachenii. Poetomu est' 6 komponent tenzora krivizny s odinakovymi i $6 \cdot {\displaystyle 5\over\displaystyle 2}= 15$ komponent s razlichnymi znacheniyami indeksov. Tri komponenty s chetyrmya razlichnymi indeksami svyazany uravneniem (7.17), poetomu vsego imeetsya 20 nezavisimyh komponent.

Sushestvuet odno differencial'noe tozhdestvo, kotoroe nazyvaetsya tozhdestvom B'yanki:

$\begin{displaymath} R^{\alpha}_{ \beta \mu \nu; \rho} + R^{\alpha}_{ \beta \rho \mu; \nu} + R^{\alpha}_{ \beta \nu \rho; \mu} =0 \end{displaymath}$

(7.18)

Iz tenzora krivizny chetvertogo ranga obrazuyutsya dopolnitel'no dve velichiny. Odna yavlyaetsya tenzorom vtorogo ranga i obrazuetsya svertkoi verhnemu i vtoromu nizhnemu indeksam:

$\begin{displaymath} R_{\mu \nu}=R^{\rho}_{. \mu \rho \nu} \end{displaymath}$

(7.19)

Tenzor Richchi yavlyaetsya simmetrichnym tenzorom, poetomu v chetyrehmernom prostranstve on imeet 10 nezavisimyh komponent (kak i metricheskii tenzor). Svertkoi po ostavshimsya dvum indeksam mozhno poluchit' skalyarnuyu velichinu, kotoraya nazyvaetsya skalyarnoi kriviznoi prostranstva:

$\begin{displaymath} R= g^{\mu \nu} R_{\mu \nu} \end{displaymath}$

(7.20)

Poskol'ku (7.20) yavlyaetsya skalyarnoi velichinoi, to ona yavlyaetsya odnovremenno invariantnoi otnositel'no koordinatnyh preobrazovanii i nazyvaetsya takzhe skalyarnoi kriviznoi prostranstva.

Iz tozhdestv B'yanki mozhno poluchit' vazhnoe ravenstvo. Dlya etogo svernem tozhdestvo (7.18) po indeksam $\alpha \rho$ . Togda poluchim uravnenie vida:

$\begin{displaymath} R^{\alpha}_{\mu \nu \lambda; \alpha} + R_{\nu \lambda; \mu} - R_{\mu \lambda; \nu} =0 \end{displaymath}$

Svernem eto uravnenie eshe raz s metricheskim tenzorom, poluchim ravenstvo:

$\begin{displaymath} \left( R_{\mu \nu} -{\displaystyle 1\over\displaystyle 2} g_{\mu \nu}R\right)^{;\mu}=0 \end{displaymath}$

(7.21)

V etom uravnenii chetyrehmernaya divergenciya nekotorogo tenzora vtorogo ranga ravna nulyu. Etot tenzor:

$\begin{displaymath} G_{\mu \nu} = R_{\mu \nu} - {\displaystyle 1\over\displaystyle 2} g_{\mu \nu} R \end{displaymath}$

(7.22)

igraet vazhnuyu rol' v obshei teorii otnositel'nosti. Inogda ego nazyvayut tenzorom Einshteina.

7.4 Variacii tenzora krivizny

Rassmotrim teper' izmenenie simvolov Kristoffelya, a takzhe tenzorov krivizny, Richchi i skalyarnoi krivizny pri variaciyah metriki. Poluchennye uravneniya my budem ispol'zovat' v dal'neishem kak dlya vyvoda uravnenii gravitacionnogo polya, tak i dlya analiza slabogo gravitacionnogo polya i slabogo gravitacionnogo polya na fone sil'nogo polya.

Pust' u nas est' metrika $g_{\alpha \beta}$ , na kotoruyu nalozheny nebol'shie izmeneniya, kotorye my budem oboznachat' $\delta g_{\alpha \beta}$ i kotorye yavlyayutsya variaciyami metriki. Otmetim, chto eti dve velichiny po otdel'nosti obrazuyut tenzora. Tem ne menee seichas my budem rassmatrivat' kak odin tenzor, kotoryi sostoit iz "fonovoi" metriki i malyh popravok:

$\begin{displaymath} g_{\alpha \beta} = g^b_{\alpha \beta} + \delta g_{\alpha \beta} \end{displaymath}$

(7.23)

Vse velichiny, kotorye my budem vychislyat' nizhe, budem vychislyat' tol'ko do pervogo poryadka malosti po variaciyam, prenebregaya vkladom variacii bolee vysokoi stepeni.

Rassmotrim kak svyazany variacii kontravariantnyh komponent metricheskogo tenzora s variaciya kovariantnyh komponent. Kontravariantnye komponenty metricheskogo tenzora udovletvoryayut ravenstvu vida:

$\begin{displaymath} g^{\alpha \rho} g_{\beta \rho} =\delta^{\alpha}_{\beta} \end{displaymath}$

Podstavlyaya syuda kovariantnyi metricheskii tenzor s variaciyami $g_{\alpha \beta} +\delta g_{\alpha \beta}$ i konravariantnye komponenty $g^{\alpha \beta} +\delta g^{\alpha \beta}$ poluchaem svyaz' mezhdu kontravariantnymi i kovariantnymi variaciyami:

$\begin{displaymath} \delta g^{\alpha \beta}= -g^{\alpha \mu} g^{\beta \nu} \delta g_{\mu \nu} \end{displaymath}$

(7.24)

Otsyuda vidno, chto konravariantnye variacii otlichayutsya ot kovariantnyh znakom, a indeksy podnimayutsya metricheskim tenzorom, kak i u lyubyh drugih tenzorov.

Dlya vychisleniya variacii opredelitelya metricheskogo tenzora vvedem absolyutno antisimmetrichnyi edinichnyi tenzor chetvertogo ranga $e^{\alpha \beta \gamma \delta}$ [8]. Tak nazyvaetsya tenzor, komponenty kotorogo menyayut znak pri perestanovke lyubyh dvuh indeksov, prichem otlichnye ot nulya komponenty ravny $\pm 1$ . Togda mozhno zapisat' opredelitel' metricheskogo tenzora kak:

$\begin{displaymath} g= {\displaystyle 1\over\displaystyle 24} e^{\alpha \beta \g... ... \epsilon} g_{\beta \zeta} g_{\gamma \eta} g_{\delta \theta} \end{displaymath}$

Teper' mozhno legko vychislit' variacii opredelitelya metricheskogo tenzora.

Variacii opredelitelya s tochnost'yu do lineinyh po $\delta g^{\alpha \beta}$ chlenov est':

$\begin{displaymath} \delta g= -g^{\alpha \beta} \delta g_{\alpha \beta } \end{displaymath}$

Privedem takzhe odnu poleznuyu formulu, soderzhashuyu variacii plotnosti metricheskogo tenzora:

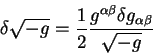
$\begin{displaymath} \delta \sqrt{-g}= {\displaystyle 1\over\displaystyle 2} {\di... ...a \beta} \delta g_{\alpha \beta}\over\displaystyle\sqrt{-g}} \end{displaymath}$

V etih dvuh uravneniyah opushen indeks v simvolah fonovoi metriki, no poskol'ku my dogovorilis' ostavlyat' tol'ko lineinye chleny po variaciyam, legko opredelit' velichiny soderzhashie etot indeks.

Rassmotrim teper' variacii simvolov Kristoffelya. Vnov' ostavlyaya tol'ko lineinye chleny po $\delta g_{\alpha \beta}$ poluchaem uravnenie dlya variacii simvolov Kristoffelya:

$\begin{displaymath} \delta \Gamma^{\mu}_{\alpha \beta}= {1 \over 2} g^{\mu \nu} ... ...beta})_{; \alpha} - (\delta g_{\alpha \beta})_{; \nu} \rbrace \end{displaymath}$

(7.25)

Otmetim, chto variacii simvolov Kristoffelya po otnosheniyu k "fonovoi" metrike $g^b_{\alpha \beta}$ yavlyayutsya tenzorami tret'ego ranga. Kovariantnye proizvodnye postroeny s pomosh'yu fonovoi metriki $g^b_{\alpha \beta}$ .

Variacii tenzora Richchi vyrazhayutsya cherez kovariantnye proizvodnye novogo tenzora - variacii simvolov Kristoffelya $\delta \Gamma^{\mu}_{\alpha \beta}$ :

$\begin{displaymath} \delta R_{\alpha \beta} = \left( \delta \Gamma^{\mu}_{\alpha... ...} - \left( \delta \Gamma^{\mu}_{\alpha \beta} \right)_{; \mu} \end{displaymath}$

(7.26)

Eto uravnenie mozhno perepisat' v terminah variacii metriki, v nih ono imeet vid:

$\begin{displaymath} \delta R_{\alpha \beta} = {1 \over 2} g^{\mu \nu}\lbrace \l... ...+ \left( \delta g_{\alpha \beta} \right)_{;\nu ;\mu} \rbrace \end{displaymath}$

(7.27)

<< 6. Analiz v neevklidovoi | Oglavlenie | 8. Uravnenie dvizheniya v >>

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe: 70 let Stivenu Hokingu Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vsemirnyi god fiziki: triumf Einshteina Al'bert Einshtein opisyvaet prostranstvo-vremya Polnoe solnechnoe zatmenie Otdel pul'sarnoi astrometrii PRAO AKC FIAN O skorosti gravitacii - ot avtorov Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce