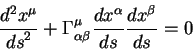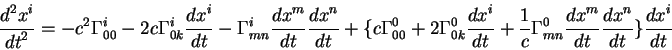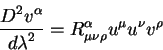Astronet > 8. Uravnenie dvizheniya v obshei teorii otnositel'nosti

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Teoriya otnositel'nosti dlya astronomov

<< 7. Tenzor krivizny | Oglavlenie | 9. Uravneniya gravitacionnogo polya >>

Razdely

8. Uravnenie dvizheniya v obshei teorii otnositel'nosti

Vliyanie gravitacionnogo polya na dvizhenie chastic v n'yutonovskoi mehanike horosho izucheno. Uravnenie dvizheniya chasticy predstavlyaet soboi uravnenie v levoi chasti kotorogo stoit uskorenie probnoi chasticy umnozhennoe na massu chasticy (v dannom sluchae eto inertnaya massa), v pravoi chasti uravneniya stoit gravitacionnaya sila. Gravitacionnaya sila, v svoyu ochered', predstavlyaet iz sebya proizvedenie massy probnoi chasticy (v dannom sluchae - gravitacionnoi massy) na uskorenie so storony tyagoteyushego tela: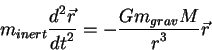

$\begin{displaymath} m_{inert}{\displaystyle d^2 \vec r\over\displaystyle dt^2}= -{\displaystyle Gm_{grav}M\over\displaystyle r^3} \vec r \end{displaymath}$

Poskol'ku inertnaya massa tela ravna ego gravitacionnoi masse (eto formulirovka principa ekvivalentnosti, mnogokratno proverennogo eksperimental'no), to dvizhenie probnoi chasticy ne zavisit ot massy etoi chasticy - pero pticy i kirpich padayut v gravitacionnom pole s odinakovym uskoreniem (konechno, esli prenebrech' soprotivleniem vozduha).

V obshei teorii otnositel'nosti rol' gravitacionnoi sily igraet krivizna prostranstva - vremeni. Dvizhenie v gravitacionnom pole - eto dvizhenie v iskrivlennom prostranstve, otklonenie ot dvizheniya po pryamoi linii - eto otklonenie v dvizhenii voznikayushee v iskrivlennom prostranstve vremeni.

Vspomnim vnachale uravneniya dvizheniya v special'noi teorii otnositel'nosti.

8.1 Uravnenie dvizheniya probnoi chasticy v STO

V special'noi teorii otnositel'nosti uravnenie dvizheniya probnoi chasticy imeet vid:

$\begin{displaymath} m_{inert}c^2{\displaystyle d u^{\alpha}\over\displaystyle ds}=F^{\alpha}, \end{displaymath}$

(8.1)

gde $u^{\alpha}$ - 4 skorost' chasticy (fizicheskoe opredelenie) ili vektor, kasatel'nyi k traektorii chasticy (matematicheskoe opredelenie). Otmetim, chto $u^{\alpha}$ - velichina bezrazmernaya, a imeet razmernost' [sm]. Drugimi slovami, sleva stoit velichina, kotoraya imeet razmernost' sily g $\cdot{\displaystyle\mbox{sm}\over\displaystyle\mbox{sek}^2}$ .

Uravneniya dvizheniya elektrona v elektromagnitnom pole imeyut vid:

$\begin{displaymath} m_e c^2 {\displaystyle d u^{\alpha}\over\displaystyle ds}=e F^{\alpha \beta} u_{\beta} \end{displaymath}$

(8.2)

Sila, kotoraya stoit v levoi chasti uravneniya yavlyaetsya 4 invariantnoi siloi Lorenca, postroennoi iz tenzora Maksvella $F^{\alpha \beta}$ .

V sluchae, kogda deistvuyushie sily ravny nulyu $F^{\alpha}=0$ , to dvizhenie chasticy proishodit po inercii. Togda reshenie uravneniya 8.1 imeet trivial'nyi vid:

$\displaystyle u^{\alpha}(s)= u^{\alpha}_0$			(8.3)
$\displaystyle x^{\alpha}(s) = u^{\alpha} \cdot s +x^{\alpha}_0$			(8.4)

Dvizhenie po inercii - eto dvizhenie po pryamoi linii. Pryamaya liniya yavlyaetsya liniei kratchaishei dliny mezhdu dvumya tochkami v evklidovoi i psevdoevklidovoi geometrii. V neevklidovoi geometrii liniya kratchaishei dliny nazyvaetsya geodezicheskoi liniei. Dvizhenie v sluchae, kogda vneshnie sily ravny nulyu, v neevklidovoi geometrii zamenyaetsya obshekovariantnym uravneniem - dvizheniem po geodezicheskoi linii.

Otmetim takzhe, chto reshenie (8.3) opisyvaet takzhe dvizhenie fotona, esli polagat', chto $u^{\alpha}$ - edinichnyi vektor v napravlenii rasprostraneniya fotona, a - afinnyi parametr vdol' traektorii.

8.2 Uravnenie dvizheniya probnoi chasticy v OTO

Dvizhenie po geodezicheskoi linii opisyvaet dvizhenie probnoi chasticy v gravitacionnom pole. Eto dvizhenie yavlyaetsya analogom dvizheniya po inercii v prostranstve s evklidovoi metrikoi.

Vypishem uravnenie dvizheniya v obshei teorii otnositel'nosti, prosto napisav kovariantnoe obobshenie uravneniya 8.1:

$\begin{displaymath} m_{inert}c^2{\displaystyle D u^{\mu}\over\displaystyle ds}=F^{\mu} \end{displaymath}$

(8.5)

Zdes' , kak my dogovorilis' vyshe, yavlyayutsya oboznacheniem kovariantnogo differenciala. Poetomu uravneniya dvizheniya v obshei teorii otnositel'nosti mozhno napisat' bolee detal'no v vide:

$\begin{displaymath} m_{inert}c^2{\displaystyle d u^{\mu}\over\displaystyle ds} +... ...c^2 \Gamma^{\mu}_{\alpha \beta} u^{\alpha} u^{\beta}=F^{\mu} \end{displaymath}$

(8.6)

Zametim, chto teper' uravneniya dvizheniya yavlyayutsya nelineinymi (po skorostyam), vtoroi chlen v levoi chasti uravnenii soderzhit kvadratichnye proizvedeniya skorostei.

Teper' uravneniya dvizheniya, naprimer, elektrona v elektromagnitnom pole imeyut vid:

$\begin{displaymath} m_e c^2 {\displaystyle D u^{\alpha}\over\displaystyle ds}=e F^{\alpha \beta} u_{\beta} \end{displaymath}$

(8.7)

Zdes' $F^{\alpha \beta}$ - tenzor elektromagnitnogo polya, a i massa i zaryad elektrona sootvetstvenno.

Otmetim, chto teper' dvizhenie probnoi chasticy v otsutstvii vneshnih sil $F^{\alpha}=0$ uzhe ne yavlyaetsya dvizheniem po pryamym liniyam, kak eto bylo v evklidovoi geometrii (8.3). Dvizhenie v otsutstvii vneshnih sil predstavlyaet iz sebya sistemu differencial'nyh uravnenii vtorogo poryadka dlya vseh chetyreh koordinat, kotorye opisyvayut chetyrehmernuyu traektoriyu probnoi chasticy.

8.2.1 Uravneniya dvizheniya v trehmernom vide

Rassmotrim uravneniya dvizheniya probnyh chastic, napisannye v trehmernom vide. Budem schitat', chto chastica yavlyaetsya nerelyativistskoi (t.e. interval mezhdu dvumya sobytiyami: vyhodom chasticy iz tochki i poyavlenie chasticy v tochke ne raven nulyu). Uravneniya dvizheniya probnyh chastic - uravneniya geodezicheskih linii imeyut vid (8.6). V kachestve afinnogo parametra vdol' geodezicheskoi vozmem - interval mezhdu sobytiyami (t.k. on ne raven nulyu). Krome togo, napomnim, chto 4 skorost' - eto edinichnyi vektor kasatel'nyi k traektorii dvizheniya, po opredeleniyu:

$\begin{displaymath} u^{\alpha}={\displaystyle d x^{\alpha}\over\displaystyle d s} \end{displaymath}$

Eto znachit, chto uravneniya dvizheniya mozhno perepisat' v vide, kotoryi soderzhit uskoreniya (vtoruyu proizvodnuyu ot koordinaty chasticy po afinnomu parametru):

$\begin{displaymath} {\displaystyle d^2 x^{\mu}\over\displaystyle ds^2} + \Gamma^... ...style ds} {\displaystyle d x^{\beta}\over\displaystyle d s}= 0 \end{displaymath}$

(8.8)

Preobrazuem vtoruyu proizvodnuyu ot koordinaty s prostranstvennym indeksom po intervalu k vtoroi proizvodnoi po koordinate s nulevym indeksom:

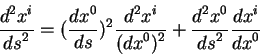
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d s^2}=({\displayst... ...splaystyle ds^2} {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}$

Zdes' $d x^0\over\displaystyle d s$ - nulevaya komponenta 4 skorosti, a $d^2 x^0\over\displaystyle ds^2$ - 4 mernoe uravnenie dvizheniya s indeksom 0.

Eto uravnenie mozhno obratit', poluchaya uravneniya dlya uskorenii probnoi chasticy v vide:

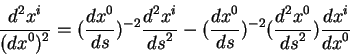
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle(d x^0)^2} = ({\disp... ...ystyle d s^2}) {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}$

Podstavim v eto uravnenie vyrazhenie dlya

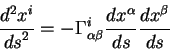
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d s^2} = - \Gamma^i... ...style d s} {\displaystyle d x^{\beta}\over\displaystyle d s} \end{displaymath}$

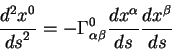
$\begin{displaymath} {\displaystyle d^2 x^0\over\displaystyle d s^2} = - \Gamma^0... ...style d s} {\displaystyle d x^{\beta}\over\displaystyle d s} \end{displaymath}$

Posle zaversheniya vseh vykladok, okonchatel'no poluchaem uravnenie dvizheniya v vide:

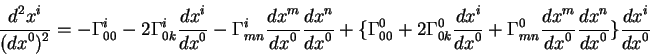
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle(d x^0)^2} = -\Gamma... ...e d x^0}\rbrace {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}$

Do sih por differencirovanie provodilos' po koordinate s nulevym indeksom, poskol'ku eta koordinata imeet takuyu zhe razmernost' kak i ostal'nye koordinaty [sm]. Odnako, dlya polucheniya obychnogo trehmernogo uravneniya dvizheniya neobhodimo pereiti k differencirovaniyu po vremeni . Umnozhim obe chasti poluchennogo uravneniya na kvadrat skorosti sveta i poluchim uravnenie dvizheniya v obychnom trehmernom vide:

$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d t^2} = -c^2 \Gamm... ...tyle d t} \rbrace {\displaystyle d x^i\over\displaystyle d t} \end{displaymath}$

(8.9)

Sravnivaya obychnoe uravnenie dvizheniya v n'yutonovskoi gravitacii:

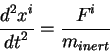
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d t^2}= {\displaystyle F^i\over\displaystyle m_{inert}} \end{displaymath}$

mozhno sdelat' vyvod o tom, chto analogom n'yutonovskoi sily yavlyaetsya chlen vida:

$\begin{displaymath} F^i_{grav}= - m_{grav} c^2 \Gamma^i_{00} \end{displaymath}$

Iz privedennogo uravneniya vidno, chto (8.9) soderzhit chleny raznyh poryadkov po otnosheniyu harakternoi skorosti dvizheniya probnoi chasticy k skorosti sveta. Samyi bol'shoi chlen - sila N'yutona, no sushestvuyut i bolee slabye sily, kotorye, tem ne menee vnosyat vklad v dvizhenie chasticy v gravitacionnom pole. Oni nazyvayutsya postn'yutonovskimi popravkami.

Bolee polnyi analiz uravnenii dvizheniya, v chastnosti vklada postn'yutonovskih popravok my prodelaem pozzhe.

8.3 Deviaciya geodezicheskii linii

Deviaciei dvuh beskonechno blizkih geodezicheskih linii nazyvaetsya otklonenie etih linii mezhdu soboi.

Rassmotrim dve beskonechno blizkie geodezicheskie linii. Odna liniya harakterizuetsya neskol'kimi parametrami. Vyberem dva iz nih. Odin parametr nazovem $\lambda$ , on budet afinnym parametrom vdol' linii. Vtoroi parametr vyberem tak, chtoby on otschityvalsya vdol' napravleniya vektora, kotoryi soedinyaet dve ukazannye geodezicheskie linii i yavlyaetsya perpendikulyarnym vektoru, kasatel'nomu pervoi geodezicheskoi linii. Etot parametr nazovem $\eta$ . Teper' uravnenie geodezicheskoi yavlyaetmya funkciei dvuh parametrov $x^{\alpha}(\lambda, \eta)$ . Pervyi parametr $\lambda$ otchityvaet dlinu vdol' geodezicheskoi, vtoroi parametr $\eta$ otschityvaet "nomer" geodezicheskoi linii, koordinatu v perpendikulyarnom napravlenii.

Vektor kasatel'nyi k traektorii geodezicheskoi linii, kak prezhde budem oboznachat' $u^{\alpha}$ . Vvedem vtoroi vektor $v^{\alpha}$ , kotoryi budet kasatel'nym k linii, soedinyayushie dve geodezicheskie. Otmetim poleznoe ravenstvo:

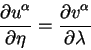
$\begin{displaymath} {\displaystyle\partial u^{\alpha}\over\displaystyle\partial ... ...ystyle\partial v^{\alpha}\over\displaystyle\partial \lambda} \end{displaymath}$

Dokazhem eshe odno ravenstvo, vazhnoe dlya nashih rassuzhdenii. Rassmotrim kovariantnuyu proizvodnuyu ot vektora $v^{\alpha}$ vdol' geodezicheskoi:

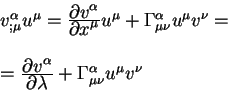
$\begin{displaymath} \begin{array}{l} v^{\alpha}_{; \mu} u^{\mu}= {\displaystyle\... ...ambda} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} v^{\nu} \end{array}\end{displaymath}$

Spomnim teper', chto vektor 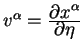$v^{\alpha}={\displaystyle\partial x^{\alpha}\over\displaystyle\partial \eta}$ . Poskol'ku mozhno pomenyat' chastnye proizvodnye mestami, to proizvodnuyu ot vektora $v^{\alpha}$ po parametru $\lambda$ mozhno zapisat', kak proizvodnuyu ot vektora $u^{\alpha}$ po parametru $\eta$ . Poetomu mozhno prodolzhit' verhnee ravenstvo kak:

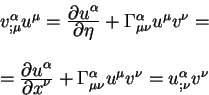
$\begin{displaymath} \begin{array}{l} v^{\alpha}_{; \mu} u^{\mu}={\displaystyle\p... ...u \nu} u^{\mu} v^{\nu} =u^{\alpha}_{;\nu}v^{\nu} \end{array} \end{displaymath}$

Teper' vypishem samo ravenstvo, kotoroe bylo dokazano:

$\begin{displaymath} v^{\alpha}_{; \mu} u^{\mu} = u^{\alpha}_{; \mu} v^{\mu} \end{displaymath}$

(8.10)

Rassmotrim teper' kak menyaetsya vektor $v^{\alpha}$ vdol' geodezicheskoi linii. Poskol'ku dlina etogo vektora yavlyaetsya rasstoyanie mezhdu geodezicheskimi, to sam vektor pokazyvaet kak menyaetsya rasstoyanie i orientaciya dvuh probnyh chastic, kotorye dvizhutsya po geodezicheskim liniyam v gravitacionnom pole. V obychnoi n'yutonovskoi teorii tyagoteniya, izmenenie rasstoyaniya mezhdu probnymi chasticami vyzyvaetsya prilivnymi silami. Naidem analog prilivnyh sil v n'yutonovskoi mehaniki v obshei teorii otnositel'nosti.

Dlya etogo rassmotrim vnachale pervuyu kovariantnuyu proizvodnuyu ot vektora $v^{\alpha}$ vdol' geodezicheskoi:

$\begin{displaymath} {\displaystyle Dv^{\alpha}\over\displaystyle d \lambda} = v^{\alpha}_{;\gamma}u^{\gamma} \end{displaymath}$

Poskol'ku proizvodnaya po parametru $\lambda$ mozhet byt' vyrazhena kak proizvodnye po koordinatam, umnozhennye na vektor vdol' geodezicheskoi. Tochno tak zhe mozhno vyrazit i vtoruyu proizvodnuyu.

Rassmotrim teper' vtoruyu proizvodnuyu ot vektora $v^{\alpha}$ vdol' geodezicheskoi:

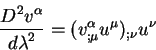
$\begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2} = (v^{\alpha}_{;\mu}u^{\mu})_{; \nu} u^{\nu} \end{displaymath}$

V etom ravenstve priem perehoda ot differencirovaniya po afinnomu parametru k differencirovaniyu po koordinatam primenen dvazhdy. Vospol'zuemsya takzhe ravenstvom (8.10) i vyrazim velichinu v kruglyh skobkah cherez proizvodnuyu ot vektora kasatel'nogo k geodezicheskoi, togda poluchim:

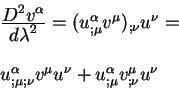
$\begin{displaymath} \begin{array}{l} {\displaystyle D^2 v^{\alpha}\over\displays... ...u^{\nu} + u^{\alpha}_{;\mu}v^{\mu}_{; \nu} u^{\nu} \end{array}\end{displaymath}$

V pervom chlene menyaem poryadok kovariantnogo differencirovaniya:

$\begin{displaymath} u^{\alpha}_{;\mu ; \nu} = u^{\alpha}_{;\nu ; \mu} - R^{\alpha}_{\rho \mu \nu} u^{\rho}, \end{displaymath}$

a ko vtoromu vnov' primenyaem ravenstvo (8.10). Poluchaem, chto vtoraya kovariantnaya proizvodnaya ot vektora $v^{\alpha}$ est':

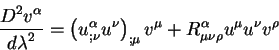
$\begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2}... ...v^{\mu} + R^{\alpha}_{\mu \nu \rho} u^{\mu} u^{\nu} v^{\rho} \end{displaymath}$

Obratim vnimanie na to, chto v tenzore krivizny izmenen poryadok indeksov, poetomu i znak pered tenzorom pomenyalsya. Pervyi chlen raven nulyub v silu uravneniya geodezicheskoi linii (sm. (6.17)).

Poetomu okonchatel'no vtoraya kovariantnaya proizvodnaya ot vektora $v^{\alpha}$ ravna:

$\begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2} = R^{\alpha}_{\mu \nu \rho} u^{\mu} u^{\nu} v^{\rho} \end{displaymath}$

(8.11)

Umnozhaya eto uravnenie na velichinu $\Delta \eta$ - rasstoyanie mezhdu geodezicheskimi poluchaem uravnenie dlya vektora, kotoryi soedinyaet dve probnye chastic, kotorye svobodno dvizhutsya po dvum blizkim geodezicheskim liniyam.

Eto uravnenie nazyvaetsya uravnenie deviacii blizkih geodezicheskih linii.

<< 7. Tenzor krivizny | Oglavlenie | 9. Uravneniya gravitacionnogo polya >>

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe: 70 let Stivenu Hokingu Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vsemirnyi god fiziki: triumf Einshteina Al'bert Einshtein opisyvaet prostranstvo-vremya Polnoe solnechnoe zatmenie Otdel pul'sarnoi astrometrii PRAO AKC FIAN O skorosti gravitacii - ot avtorov Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce