Astronet > Luna - sputnik ili planeta?

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Luna - sputnik ili planeta?

K.V.HOLShEVNIKOV

Sankt-Peterburgskii gosudarstvennyi universitet

Inogda professionaly otnosyat Lunu k samostoyatel'nym planetam Solnechnoi sistemy, poskol'ku sushestvuet neskol'ko kriteriev razlicheniya planet i sputnikov. Osnovnaya cel' stat'i - rasskazat' ob etih kriteriyah, o vazhnyh dlya astronomii i kosmonavtiki gravitacionnyh sferah.

Vvedenie

-	Eto chto, vopros dlya KVN ili KVAS (Klub Veselyh Astronomov, kak govoryat v Kourovke na studencheskih zimnih astronomicheskih shkolah)?
-	Net, ya ser'ezno.
-	Prekrasno! Izdatel'stvo "Malysh" etazhom nizhe.

Pohozhii razgovor vpolne mog sostoyat'sya eshe v III veke do n.e. Ved' uzhe Aristarh Samosskii obosnoval dvizhenie Luny vokrug Zemli, a menee yarkih bluzhdayushih svetil i Zemli vokrug Solnca. I tem ne menee vynesennyi v zagolovok vopros otnyud' ne tak prost, kak kazalos' Aristarhu i Koperniku. Podobno elektronu, proyavlyayushemu svoistva kak chasticy, tak i volny, Luna v svoem dvizhenii proyavlyaet svoistva kak sputnika, tak i planety. Obosnovaniyu etogo neprivychnogo dlya mnogih utverzhdeniya i posvyashena nastoyashaya stat'ya.

Matematicheskaya model'

Na dvizhenie Luny vliyaet massa yavlenii: prityazhenie kol'ca Saturna, Magellanovyh oblakov, udary meteoritov i kosmicheskih apparatov. No dlya otveta na vynesennyi v zagolovok vopros dostatochno uchest' lish' glavnye prichiny, opredelyayushie kachestvennoe povedenie lunnoi orbity. Okazyvaetsya, mozhno ogranichit'sya sleduyushei prostoi model'yu: na Lunu deistvuet tol'ko n'yutonovskoe prityazhenie Zemli i Solnca, prichem vse tri tela mozhno schitat' material'nymi tochkami. Dokazhem eto utverzhdenie.

Po zakonu vsemirnogo tyagoteniya lyuboe svetilo prityagivaet Lunu slabee, chem Solnce, v k raz,

$k=\frac{m_{1}r_{2}^{2}}{m_{2}r_{1}^{2}}$ .

(1)

Zdes' m₁ , m₂ - massy Solnca i svetila; r₁ , r₂ - rasstoyaniya ot Luny do etih tel. Yasno, chto hot' kakuyu-to konkurenciyu Zemle i Solncu mogut sostavit' lish' bol'shie planety Solnechnoi sistemy, a zvezdy, tumannosti, meteority, relyativistskie effekty i prochee mozhno ostavit' poetam.

Sredi planet zemnoi gruppy naibol'shei massoi m₂ i odnovremenno naimen'shim iz vozmozhnyh rasstoyanii r₂ obladaet Venera, dlya ostal'nyh planet etu rol' ispolnyaet Yupiter. Znachenie k dlya Venery minimal'no pri odnovremennom vypolnenii sleduyushih uslovii: Venera v afelii; Zemlya v perigelii; Luna v apogee; nablyudayutsya kol'ceobraznoe solnechnoe zatmenie i nizhnee soedinenie Venery. Analogichno v sluchae Yupitera dolzhno byt': Yupiter v perigelii; Zemlya v afelii; Luna v apogee; nablyudayutsya polnoe lunnoe zatmenie i protivostoyanie Yupitera. Podstavlyaya v (1) sootvetstvuyushie znacheniya mass i rasstoyanii [1], poluchim

k (Venera) $\geq$ 27 $\cdot$ 10³, k (Yupiter) $\geq$ 16 $\cdot$ 10³.

Poluchennye ocenki otnositel'nyh velichin sil (ili, chto to zhe, uskorenii) opisyvayut ih vliyanie na traektoriyu Luny v inercial'noi ili blizkoi k nei geliocentricheskoi sisteme otscheta. No chashe vsego nas interesuet geocentricheskoe dvizhenie, i tut samoe vremya vspomnit' o lifte Einshteina. Sila, privodyashaya k uskoreniyu dazhe v parsek za kvadratnuyu sekundu, nikak ne otrazitsya na dvizhenii Luny otnositel'no Zemli, esli eto uskorenie odinakovo dlya oboih tel, inymi slovami, esli silovoe pole odnorodno. Effekty v geocentricheskom dvizhenii vyzyvayutsya raznost'yu uskorenii polya v tochkah, gde nahodyatsya centry mass Luny i Zemli. Podobnye raznosti prinyato nazyvat' prilivnymi uskoreniyami, svoistva i rol' kotoryh v zhizni Vselennoi prekrasno opisany v [2]. V chastnosti,

$\Phi = \frac{2Gm_{1} \rho}{r_{1}^{3}}$ .

(2)

Zdes' $\Phi$ - naibol'shee znachenie modulya vyzyvaemogo Solncem prilivnogo uskoreniya v geocentricheskom dvizhenii Luny pri vseh myslimyh polozheniyah poslednei na rasstoyanii r₁ ot Solnca i $\rho$ ot Zemli. Formula (2), razumeetsya, opisyvaet prilivnoe vliyanie lyubogo tela, nado tol'ko izmenit' znacheniya m₁ , r₁ .

Oboznachaya cherez k₀ = (r₂ / r₁)k otnoshenie $\Phi$ dlya Solnca i kakoi-libo planety, poluchim

k₀(Venera) $\geq$ 7 $\cdot$ 10³, k₀(Yupiter) $\geq$ 60 $\cdot$ 10³.

Do sih por my schitali nebesnye tela tochkami ili, chto to zhe, telami sfericheskoi struktury - sharami s plotnost'yu, zavisyashei lish' ot rasstoyaniya do centra. Gravitacionnoe uskorenie, induciruemoe proizvol'nym telom konechnyh razmerov, mozhet sushestvenno otlichat'sya ot takovogo dlya shara. No, kak zametili eshe drevnie sofisty, izdali lyubaya bashnya kazhetsya krugloi. V nashem sluchae, soglasno [3], pryamoe solnechnoe prityazhenie prevyshaet effekt szhatiya Zemli po krainei mere v 1,9 $\cdot$ 10⁶ raz, a prilivnoe - v 9 $\cdot$ 10³ raz. Itak, v kachestvennom opisanii dvizheniya Luny dostatochno priblizheniya zadachi treh tel (tochek).

Gravitacionnye sfery

V nebesnoi mehanike i kosmonavtike chasto pol'zuyutsya udobnym ponyatiem gravitacionnoi sfery. Pust' maloe telo P (Luna) dvizhetsya v n'yutonovskom pole tel Q₁ (Solnce) i Q (Zemlya) massami m₁ i m sootvetstvenno. Prostranstvo vozmozhnyh polozhenii P mozhno razbit' na dve chasti: oblast' T, gde dominiruet prityazhenie Q, i ostal'noe prostranstvo T₁ . Oblast' T nazyvayut gravitacionnoi sferoi Q po otnosheniyu k Q₁ . Chasto tak zhe nazyvayut i granicu S mezhdu T i T₁ , chto ne privodit k putanice.

Privedennoe opredelenie stanovitsya polnym, kak tol'ko my pridadim tochnyi smysl ponyatiyu "dominirovat'". Polezny razlichnye traktovki poslednego, tak chto v astronomii neskol'ko gravitacionnyh sfer.

Raspolozhenie tel opishem vektorami R = Q₁Q, r = Q₁P, $\rho$ = QP (ris. 1). Ih moduli budem oboznachat' temi zhe, no ne zhirnymi bukvami.

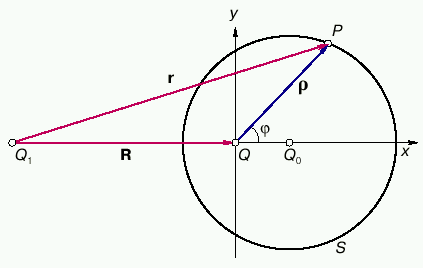Ris. 1.Sfera tyagoteniya

Sfera tyagoteniya

Tak nazyvaetsya prosteishaya iz gravitacionnyh sfer S, vydelyaemaya usloviem: sily prityazheniya tochki P so storony Q₁ i Q ravny mezhdu soboi:

$m_{1} \rho^{2} = mr^{2}$ .

(3)

Provedem os' x dekartovoi sistemy koordinat cherez tochki Q₁ , Q. Nachalo otscheta sovmestim s Q. Polozheniya osei y, z bezrazlichny. Zapishem koordinaty treh interesuyushih nas vektorov:

R = (R, 0, 0) $\rho$ = (x, y, z) r = R + $\rho$ = (R + x, y, z).

Uravnenie (3) elementarno preobrazuetsya k vidu

(x - A)² + y² + z² = B²,

(4)

gde

A= $\frac{\mu}{1-\mu}R$ , B= $\frac{\sqrt{\mu}}{1-\mu}R$ , $\mu=\frac{m}{m_{1}}$

Poskol'ku $0<\mu<1$ , to $0<\mu<\sqrt{\mu}$ , 0 < A < B.

Soglasno (4) , sfera tyagoteniya okazalas' geometricheskoi sferoi. Ee radius raven B, a centr raspolozhen v tochke Q₀ na osi x na rasstoyanii A sprava ot Q, prichem Q lezhit vnutri S. Oblast' T - shar, vnutrennost' S. Risunok 1 izobrazhaet sechenie S ploskost'yu xy. Sfera S dvizhetsya vmeste s telami Q₁ , Q i menyaet svoi razmery vmeste s R (parametr $\mu$ postoyanen).

Dlya pary Solnce-Zemlya velichina R kolebletsya ot 0,983 a.e. (a.e. - astronomicheskaya edinica), zimoi do 1,017 a.e. letom. Sootvetstvenno A i B izmenyayutsya v predelah 442 $\leq$ A $\leq$ 457 km, 255 $\cdot$ 10³ $\leq$ B $\leq$ 264 $\cdot$ 10³ km. Smeshenie A centra Q₀ ot Q okazalos' v 14 raz men'she radiusa Zemli, i im mozhno prenebrech'. No eto malointeresno. Zamechatel'no, chto B pochti vdvoe men'she rasstoyaniya Zemlya-Luna! Luna nahoditsya vne sfery tyagoteniya Zemli, prichem dostatochno daleko. V svyazi s etim mozhno upomyanut', chto Solnce prityagivaet Lunu v dva raza sil'nee Zemli.

Itak, s tochki zreniya sfery tyagoteniya Luna - planeta, a ne sputnik. Esli vnezapno ostanovit' Zemlyu, to Luna brosit ee i budet prodolzhat' odna svoi obychnyi put' vokrug Solnca.

Sfera deistviya

Opredelenie vvedennoi P. Laplasom sfery deistviya mnogo slozhnee. Dlya prostoty prenebrezhem massoi Luny. Predstavim uskorenie w Luny v nevrashayusheisya sisteme otscheta s centrom v Zemle v vide

w = W + Z,

(5)

gde W - nevozmushennoe uskorenie ot prityazheniya Zemli, a Z - vozmushayushee ot deistviya Solnca. Po pravilu lifta Einshteina Z est' raznost' uskorenii, vyzyvaemyh Solncem v tochkah P i Q. My uzhe znaem, chto poslednie velichiny primerno v dva raza bol'she W, no ih raznost' mala. Pri fiksirovannom $\rho$ znachenie Z s ochevidnost'yu maksimal'no vo vremya solnechnogo zatmeniya, kogda r = R - $\rho$ . Pryamoi podschet daet

$\frac{Z}{W} \leq \frac{2\rho^{3}}{\mu R^{3}} \leq 0,0094.$

(6)

Esli v (5) prenebrech' slagaemym Z, poluchim prostoe differencial'noe uravnenie, opisyvayushee zadachu dvuh tel, reshennuyu eshe N'yutonom. Dobavochnoe uskorenie Z vnosit vozmushenie v ellipticheskoe dvizhenie Luny tem men'shee, chem men'she otnoshenie Z / W.

Povtorim te zhe rassuzhdeniya v geliocentricheskoi sisteme otscheta, zameniv (5) na

w₁ = W₁ + Z₁ .

(7)

Uskorenie w₁ Luny razbito na nevozmushennoe W₁ ot prityazheniya Solnca i vozmushayushee Z₁ , vyzvannoe deistviem Zemli. Legko pokazat', chto

$\frac{Z_{1}}{W_{1}} \approx \frac{\mu r^{2}}{\rho^{2}}\approx \frac{\mu R^{2}}{\rho^{2}}\approx 0,51$ .

(8)

Sopostavim ocenki (6) i (8): vozmusheniya geliocentricheskogo ellipsa lunnoi orbity v 54 raza prevoshodyat vozmusheniya geocentricheskogo ellipsa. Naglyadnost' etomu rezul'tatu pridaet ponyatie sfery deistviya. Poslednyaya opredelyaetsya kak poverhnost' S, na kotoroi

$\frac{Z}{W} = \frac{Z_{1}}{W_{1}}$ .

(9)

Vnutri sfery deistviya, to est' v oblasti T, zadavaemoi sootnosheniem (9) s zamenoi znaka ravenstva na znak "men'she", vygodnee pol'zovat'sya uravneniyami (5), vne - uravneniyami (7). Ocenki (6), (8) pokazyvayut, chto Luna nahoditsya gluboko vnutri sfery deistviya Zemli.

Takim obrazom, s tochki zreniya sfery deistviya Luna - sputnik, a ne planeta.

Issleduem formu sfery deistviya. Zapishem ee uravnenie (9) v toi zhe sisteme koordinat, v kotoroi polucheno (4). Posle preobrazovanii

$\rho^{8}(R^{4} + r^{4} - 2rR {\mathbf{rR}}) = \mu^{4} r^{8}(R^{4} + \rho^{4} + 2\rho R {\mathbf{\rho R}}),$

(10)

gde

$\rho^{2} = x^{2} + y^{2} + z^{2}\,, \qquad r^2 = (x+R)^2 + y^2 + z^2,$

$\mathbf{\rho R} = Rx, \qquad {\mathbf{rR}} = r(R+x).$

Poskol'ku uravnenie (10) soderzhit y, z tol'ko v kombinacii y² + x², to S est' poverhnost' vrasheniya vokrug osi x. Poetomu forma S opredelyaetsya formoi krivoi S' - secheniem S ploskost'yu xy.

Preobrazuya (10) sredstvami komp'yuternoi algebry, student astronomicheskogo otdeleniya Leningradskogo universiteta S.R. Tyurin[4] nashel, chto S' sovpadaet ili yavlyaetsya chast'yu algebraicheskoi krivoi 48-i stepeni ot x, y. Mozhno pokazat', chto S' predstavlyaet soboi blizkii k krugu, simmetrichnyi otnositel'no obeih osei oval, szhatyi po osi x (osi zatmenii). Rasstoyanie $\rho$ izmenyaetsya ot 792 $\cdot$ 10³ do 940 $\cdot$ 10³ km, chto v dva raza prevyshaet naibol'shii radius lunnoi orbity.

Sfera hilla

Dlya prostoty budem prenebregat' massoi Luny i ekscentrisitetom zemnoi orbity. Kak pokazal V.G. Golubev [5], bez etih predpolozhenii mozhno oboitis', no my ne budem uslozhnyat' zadachu.

Utochnim napravlenie osi y. Provedem ee v ploskosti krugovoi orbity Q v storonu dvizheniya. Nachalo Q sistemy xyz opisyvaet okruzhnost' radiusa [m₁ / (m₁ + m)]R vokrug centra mass Q₁ i Q, a sama sistema ravnomerno vrashaetsya vokrug osi z s uglovoi skorost'yu $\omega$ , opredelyaemoi po tret'emu zakonu Keplera. Dvizhenie P v sisteme xyz vyzyvaetsya silami prityazheniya k Q₁ i Q, a takzhe centrobezhnoi i koriolisovoi siloi inercii. Kak izvestno, koriolisova sila ne proizvodit raboty, a ostal'nye tri sily konservativny. Poetomu sohranyaetsya summa kineticheskoi i potencial'noi energii P, skladyvayusheisya iz energii sil prityazheniya i centrobezhnoi. Posle sokrasheniya na massu P mozhno zapisat'

$\frac{\upsilon^{2}}{2} = \frac{Gm_{1}}{r} + \frac{Gm}{\rho}+ \frac{\omega^{2}}{2}\left[ \left(\frac{m_{1}}{m_{1}+m} R + x \right)^{2} +y^{2}\right]$ -

$\frac{G(m_{1}+m}{2R} h$ .

(11)

Zdes' $\upsilon$ - skorost' P, h - bezrazmernaya postoyannaya, nazyvaemaya postoyannoi Yakobi v chest' poluchivshego integral dvizheniya (11) nemeckogo uchenogo. Poskol'ku $\upsilon^{2} \geq$ 0, to sprava v (11) stoit velichina, neotricatel'naya vo vse vremya dvizheniya.

Chast' prostranstva, vydelyaemuyu sootvetstvuyushim neravenstvom, nazyvayut oblast'yu vozmozhnyh dvizhenii. Ee granica S zadaetsya uravneniem

$\frac{2m_{1}R}{r} + \frac{2mR}{\rho} + \frac{m_{1} + m}{R^{2}}\left[\left(\frac{m_{1}}{m_{1}+m}R +x \right)^{2} + y^{2} \right]=$

= $(m_{1} +m)h$

(12)

i nazyvaetsya poverhnost'yu nulevoi skorosti ili poverhnost'yu Hilla v chest' amerikanskogo astronoma i matematika, kotoryi vvel eto ponyatie.

Ochevidno, pri bol'shih h poverhnost' Hilla imeet okruzhayushuyu Q komponentu S₀ , blizkuyu k sfere $\rho = 2\mu R / h(1 + \mu)$ . S umen'sheniem h uvelichivaetsya S₀ .

Sferoi Hilla nazyvayut naibol'shuyu iz vypuklyh poverhnostei S₀ , okruzhayushih Q. V nashem sluchae sfera Hilla predstavlyaet soboi kvazisferu, radius kotoroi menyaetsya ot 940 $\cdot$ 10³ do 1500 $\cdot$ 10³ km.

Takim obrazom, Luna dvizhetsya gluboko vnutri sfery Hilla i s etoi tochki zreniya yavlyaetsya sputnikom Zemli.

Krivizna traektorii

Geocentricheskaya orbita Luny - prostranstvennaya krivaya. No ee "prostranstvennost'" nevelika. Vektory skorosti i uskoreniya obrazuyut s ploskost'yu ekliptiki ugly ne bolee 6°. To zhe verno i dlya geliocentricheskoi traektorii. Poetomu v oboih sluchayah dostatochno ogranichit'sya proekciei orbity na ploskost' ekliptiki. Kak horosho izvestno, orbita Luny otnositel'no Zemli blizka k keplerovskomu ellipsu. Kstati, my proillyustrirovali eto, oceniv Z / W v predydushem razdele. Proekciya lezhashego v ploskosti $\Pi$ ellipsa na ortogonal'nuyu $\Pi$ ploskost' $\Pi_{1}$ - otrezok, proekciya na lyubuyu druguyu ploskost' tozhe ellips. Poetomu proekciya L geocentricheskoi orbity Luny na ploskost' ekliptiki blizka k ellipsu. Otkloneniya ot nego mozhet zametit' na glaz lish' hudozhnik ili chertezhnik. Tol'ko odno otlichie zametno prosto cheloveku s normal'nym zreniem: orbita ne zamykaetsya posle oborota vokrug Zemli. Kazhdyi sleduyushii vitok chut'-chut' smeshen po otnosheniyu k predydushemu. No eto nesushestvenno. Dlya nashei celi vazhny dva obstoyatel'stva:

vektor skorosti na L vrashaetsya vlevo, esli smotret' s severnogo polyusa ekliptiki; krivizna vsegda polozhitel'na, tochki peregiba ne vstrechayutsya;
na odnom vitke L vokrug Zemli otsutstvuyut petli.

Oba svoistva vmeste oznachayut, chto L vsegda obrashena vognutost'yu k Zemle, ne imeya ni voln (krivizna vsegda polozhitel'na), ni petel' na odnom vitke (krivizna ne slishkom velika), i pohozha na oval s zaklyuchennoi vnutri Zemlei (ris. 2). Interesno, chto oba ukazannyh svoistva (s zamenoi slova "Zemlya" na slovo "Solnce") spravedlivy i dlya proekcii geliocentricheskoi orbity Luny. Takim obrazom, s tochki zreniya krivizny traektorii Luna s ravnym pravom mozhet schitat'sya i sputnikom i planetoi.

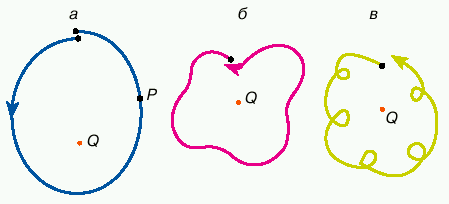Ris. 2. Geocentricheskie traektorii Luny (a); orbita znakoperemennoi krivizny (b ); petlyayushaya orbita (v)

Zaklyuchenie

My postroili matematicheskuyu model' dvizheniya Luny, adekvatnuyu zadache. Eto postroenie demonstriruet obshee pravilo, upomyanutoe, naprimer, v [6]. Vo-pervyh, my iz obshih soobrazhenii otobrali fakty, kotorye v principe mogut igrat' hot' kakuyu-to rol' v izuchaemom yavlenii, i otbrosili prakticheski beskonechnuyu sovokupnost' ostal'nyh. Vo-vtoryh, my ocenili sravnitel'noe deistvie otobrannyh i takzhe otbrosili ih vse, za isklyucheniem dvuh osnovnyh. Poslednie neobhodimo uchityvat' obyazatel'no, inache model' poteryaet svyaz' s deistvitel'nost'yu.

My rassmotreli nashu model' s raznyh storon, vvedya neskol'ko ponyatii, poleznyh i vo mnogih drugih otnosheniyah. I vyyasnili sleduyushee. V bol'shinstve sluchaev Lunu sleduet schitat' sputnikom Zemli, kak eto i delayut podavlyayushee bol'shinstvo ee gramotnyh zhitelei. No byvayut situacii, kogda Luna vedet sebya kak planeta, naprimer ona vmeste s Veneroi nahoditsya vne sfery tyagoteniya Zemli. Nakonec, vstrechayutsya situacii, kogda Luna vedet sebya odnovremenno i kak sputnik i kak planeta, naprimer formy ee geocentricheskoi i geliocentricheskoi traektorii shozhi. Vse eto sluzhit prevoshodnoi illyustraciei togo, chto ne tol'ko v kvantovoi mehanike, kazalos' by, vzaimoisklyuchayushie utverzhdeniya oba okazyvayutsya vernymi.

Zametim, chto nashi rassuzhdeniya primenimy i k drugim sputnikam planet. Naprimer, prakticheski vse iskusstvennye sputniki Zemli nahodyatsya gluboko vnutri sfery ee tyagoteniya. Tak chto ISZ - nastoyashie sputniki s tochki zreniya lyubyh gravitacionnyh sfer. I s tochki zreniya formy traektorii tozhe: ih geliocentricheskie orbity volnisty. Sputniki drugih planet lyuboznatel'nyi chitatel' mozhet issledovat' sam.

Literatura


[1]	Astronomicheskii ezhegodnik na 1997 g. / Red. V.K. Abalakin. SPb.: ITA RAN, 1996.
[2]	Surdin V.G. Prilivnye yavleniya vo Vselennoi // Novoe v zhizni, nauke, tehnike. Ser. Kosmonavtika, astronomiya. M.: Znanie, 1986. No 2.
[3]	Antonov V.A., Timoshkova E.I., Holshevnikov K.V. Vvedenie v teoriyu n'yutonovskogo potenciala. M.: Nauka, 1988.
[4]	Tyurin S.R. Issledovanie tochnogo uravneniya sfery deistviya // Tez. dokl. na stud. nauch. konf. "Fizika Galaktiki", 1989 g. Sverdlovsk, Izd-vo UrGU, 1989. S. 23.
[5]	Golubev V.G., Grebenikov E.A. Problema treh tel v nebesnoi mehanike. M.: Izd-vo MGU, 1985.
[6]	Neimark Yu.I. Prostye matematicheskie modeli i ih rol' v postizhenii mira// Sorosovskii Obrazovatel'nyi Zhurnal. 1997. No 3. S. 139-143.

Publikacii s klyuchevymi slovami: sfery gravitacionnogo vliyaniya - sputniki planet - Nebesnaya mehanika - Luna - planety Publikacii so slovami: sfery gravitacionnogo vliyaniya - sputniki planet - Nebesnaya mehanika - Luna - planety
Sm. takzhe: Zahod Zemli s "Oriona" Apollon-12 i Serveior-3 Naidite cheloveka na Lune "Muna Liza" Luna v poslednei chetverti i zvezdy-sestry Luna, pohozhaya na Saturn Yuzhnyi lunnyi peizazh Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce