Goryachie "chernye dyry". Novoe v ponimanii prirody teploty
D.A.KIRZhNIC
Moskovskii gosudarstvennyi universitet im. M.V. Lomonosova
|
Daetsya kratkii nauchno-populyarnyi obzor odnogo iz krupneishih dostizhenii astrofiziki poslednih dvuh desyatiletii - sozdaniya termodinamiki gipoteticheskih nebesnyh ob'ektov "chernyh dyr", kotoraya opisyvaet ih neobychnye teplovye svoistva. Obsheizvestnyi mehanizm poyavleniya tepla - haoticheskoe dvizhenie chastic nagretogo tela - okazyvaetsya daleko ne edinstvennym. |
| ||||
Sredi velikogo mnogoobraziya nebesnyh tel osoboe mesto zanimaet klass ob'ektov, nazyvaemyh chernymi dyrami (ChD). Ih pole tyagoteniya stol' veliko, chto nikakaya chastica, vklyuchaya chasticu (kvant) sveta, ne mozhet vyrvat'sya iznutri takogo ob'ekta i uiti na beskonechnost'. Poetomu ego poverhnost' deistvuet kak svoego roda klapan, propuskayushii veshestvo lish' v odnu storonu - vnutr' ChD (otsyuda i eto nazvanie: veshestvo valitsya v ChD kak v dyru, a svet iz nee vyiti ne v sostoyanii). Eto unikal'noe svoistvo ChD pryamo vedet k udivitel'nomu faktu - vneshnemu nablyudatelyu ona predstavlyaetsya kak goryachee telo, sluzhashee istochnikom teplovogo izlucheniya. Eto i drugie teplovye svoistva ChD opisyvayutsya special'noi teoriei - termodinamikoi chernyh dyr, kratkii ocherk kotoroi i sostavlyaet soderzhanie stat'i.
1. Chernye dyry
Nebesnye tela so svoistvami ChD rassmatrivalis' v ramkah mehaniki N'yutona eshe v XVIII veke kak ob'ekty, vtoraya kosmicheskaya skorost' kotoryh (neobhodimaya, chtoby lyuboe telo pokinulo ih poverhnost' i ushlo na beskonechnost')![]() prevyshaet skorost' sveta c = 3
prevyshaet skorost' sveta c = 3 ![]() 1010 sm/s. Zdes' G = 6,7
1010 sm/s. Zdes' G = 6,7 ![]() 10- 8 erg
10- 8 erg ![]() sm/g2 - postoyannaya tyagoteniya, M - massa ob'ekta, R - ego radius. Privedennomu usloviyu udovletvoryaet ob'ekt, massa kotorogo skoncentrirovana v ochen' malom ob'eme s radiusom
sm/g2 - postoyannaya tyagoteniya, M - massa ob'ekta, R - ego radius. Privedennomu usloviyu udovletvoryaet ob'ekt, massa kotorogo skoncentrirovana v ochen' malom ob'eme s radiusom
|
|
(1) |
gde ![]() - tak nazyvaemyi gravitacionnyi radius tela,
- tak nazyvaemyi gravitacionnyi radius tela, ![]() = 2
= 2 ![]() 1033 g - massa Solnca. Sferu radiusa
1033 g - massa Solnca. Sferu radiusa ![]() nazyvayut gorizontom sobytii: imenno eyu ogranicheno pole zreniya vneshnego nablyudatelya, lishennogo informacii o ee vnutrennei chasti. Uslovie (1) okazalos' spravedlivym i v ramkah obshei teorii otnositel'nosti.
nazyvayut gorizontom sobytii: imenno eyu ogranicheno pole zreniya vneshnego nablyudatelya, lishennogo informacii o ee vnutrennei chasti. Uslovie (1) okazalos' spravedlivym i v ramkah obshei teorii otnositel'nosti.
Dlya podavlyayushei chasti nebesnyh tel eto uslovie rezko narusheno. Tak, dlya Solnca (radius 7 ![]() 105 km) i Zemli (massa 6
105 km) i Zemli (massa 6 ![]() 1027 g, radius 6
1027 g, radius 6 ![]() 103 km) velichina rg sostavlyaet sootvetstvenno vsego 3 km i 1 sm. Eshe kontrastnee sootvetstvuyushie cifry dlya "zemnyh" ob'ektov. Poetomu ChD voznikaet lish' pri kraine neobychnyh usloviyah sverhvysokoi plotnosti veshestva. Takie usloviya imeyutsya prezhde vsego na konechnom etape evolyucii zvezd s massoi, prevyshayushei primerno 3
103 km) velichina rg sostavlyaet sootvetstvenno vsego 3 km i 1 sm. Eshe kontrastnee sootvetstvuyushie cifry dlya "zemnyh" ob'ektov. Poetomu ChD voznikaet lish' pri kraine neobychnyh usloviyah sverhvysokoi plotnosti veshestva. Takie usloviya imeyutsya prezhde vsego na konechnom etape evolyucii zvezd s massoi, prevyshayushei primerno 3![]() : neuderzhimoe gravitacionnoe szhatie takoi zvezdy - kollaps vedet v konechnom schete k vypolneniyu usloviya i (1) obrazovaniyu zvezdnoi ChD. Massa takih ob'ektov lezhit v diapazone ot 3 do 100
: neuderzhimoe gravitacionnoe szhatie takoi zvezdy - kollaps vedet v konechnom schete k vypolneniyu usloviya i (1) obrazovaniyu zvezdnoi ChD. Massa takih ob'ektov lezhit v diapazone ot 3 do 100![]() . Bolee tyazhelye massivnye i sverhmassivnye ChD s massami do 108
. Bolee tyazhelye massivnye i sverhmassivnye ChD s massami do 108![]() voznikayut v rezul'tate kollapsa bol'shih mass gaza v centre sharovyh skoplenii, yadrah galaktik i kvazarah. Legkie zhe ChD s massami do 3
voznikayut v rezul'tate kollapsa bol'shih mass gaza v centre sharovyh skoplenii, yadrah galaktik i kvazarah. Legkie zhe ChD s massami do 3![]() mogli by obrazovat'sya v rezul'tate narastaniya fluktuacii plotnosti sverhszhatogo veshestva rannei Vselennoi (pervichnye ChD).
mogli by obrazovat'sya v rezul'tate narastaniya fluktuacii plotnosti sverhszhatogo veshestva rannei Vselennoi (pervichnye ChD).
Absolyutno tverdyh dokazatel'stv sushestvovaniya ChD v kosmose poka net. Odnako bol'shinstvo uchenyh shodyatsya na tom, chto rentgenovskie istochniki v nekotoryh dvoinyh sistemah predstavlyayut soboi zvezdnye ChD, a aktivnost' mnogih (esli ne vseh) yader galaktik i kvazarov - rezul'tat sushestvovaniya massivnyh i sverhmassivnyh ChD v centrah etih ob'ektov.
Predshestvennik ChD (massivnaya zvezda, gaz, fluktuaciya plotnosti) obladaet mnozhestvom nablyudaemyh parametrov, otnosyashihsya kak k ego global'nym svoistvam, tak i k harakteristikam ee vnutrennego stroeniya. Informaciya o podavlyayushei chasti takih parametrov teryaetsya vneshnim nablyudatelem v processe obrazovaniya ChD, kotoraya, kak uzhe podcherkivalos', ne vypuskaet iznutri sebya nikakih signalov, harakterizuyushih sostav i strukturu veshestva, raspredelenie elektricheskih tokov i dr. Etot fakt obrazno opisyvayut slovami "ChD ne imeet volos". Fakticheski nablyudatel' mozhet izmerit' lish' takie global'nye harakteristiki ChD, kak ee massa M, vrashatel'nyi moment i polnyi elektricheskii zaryad Q.
2. Effekt Hokinga
Narisovannaya vyshe kartina ChD imeet klassicheskii, nekvantovyi harakter. Kvantovaya mehanika vnosit v nee nekotorye korrektivy: pri sohranenii gorizonta sobytii ChD perestaet byt' "chernoi", stanovyas' istochnikom izlucheniya. Ono imeet tu zhe prirodu, chto i elektron-pozitronnye pary, rozhdaemye sil'nym elektricheskim polem, kotoroe uvelichivaet energiyu virtual'nyh (korotkozhivushih) par v vakuume, prevrashaya ih v real'nye (dolgozhivushie). Analogichno rozhdaet pary (v tom chisle i pary fotonov) i sil'noe pole tyagoteniya ChD, deistvuyushee na chasticy lyubogo sorta. Odin iz komponentov pary stanovitsya real'noi chasticei snaruzhi (i vblizi) gorizonta sobytii i, imeya polozhitel'nuyu energiyu, mozhet uiti na beskonechnost', drugaya poyavlyaetsya vnutri (i vblizi) gorizonta i padaet s otricatel'noi energiei vnutr' ChD (ris. 1).
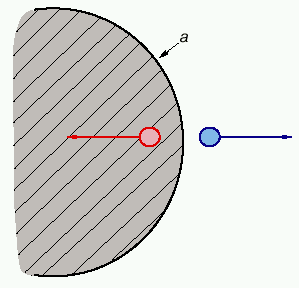 |
| Ris. 1. Rozhdenie par chastic v pole chernoi dyry. a - gorizont sobytii. Zashtrihovana chernaya dyra |
V itoge ChD stanovitsya istochnikom nepreryvnogo potoka chastic, uhodyashego na beskonechnost'. Podcherknem, chto pri formirovanii takogo izlucheniya nikakaya chastica ne peresekaet gorizonta sobytii, kotoryi tem samym po-prezhnemu obladaet svoistvami klapana.
V 1974-1975 godah angliiskii teoretik S. Hoking provodil vychisleniya harakteristik izlucheniya ChD, rukovodstvuyas' narisovannoi vyshe fizicheskoi kartinoi. K svoemu udivleniyu on obnaruzhil, chto svoistva takogo izlucheniya v tochnosti takie zhe, kak u izlucheniya goryachego chernogo tela radiusa rg , nagretogo do temperatury
|
|
(2) |
gde ![]() erg/K - postoyannaya Bol'cmana. Primechatel'no, chto v opisannom yavlenii, kotoroe nazyvayut effektom Hokinga, temperatura obratno proporcional'na masse. V processe izlucheniya massa ChD umen'shaetsya, a ee temperatura rastet, chto usilivaet izluchenie i tem samym uskoryaet ubyl' massy. Poetomu so vremenem ChD "razgoraetsya", ee temperatura bystro rastet i za konechnoe vremya
erg/K - postoyannaya Bol'cmana. Primechatel'no, chto v opisannom yavlenii, kotoroe nazyvayut effektom Hokinga, temperatura obratno proporcional'na masse. V processe izlucheniya massa ChD umen'shaetsya, a ee temperatura rastet, chto usilivaet izluchenie i tem samym uskoryaet ubyl' massy. Poetomu so vremenem ChD "razgoraetsya", ee temperatura bystro rastet i za konechnoe vremya
|
|
(3) |
ChD prekrashaet sushestvovanie, ischerpav svoyu massu.
Sushestvenno, chto poslednie mgnoveniya pered ischeznoveniem ChD budut protekat' v rezhime moshnogo vzryva s vydeleniem energii poryadka 1030 erg za vremya poryadka 0,1 s. Takie vzryvy mozhno bylo by nablyudat' i na bol'shom udalenii ot Zemli. Vprochem, eto ne otnositsya k zvezdnym i tem bolee massivnym i sverhmassivnym ChD: uzhe pri ![]() temperatura sostavlyaet nichtozhnye doli gradusa, a vremya zhizni ChD namnogo bol'she vremeni sushestvovaniya Vselennoi (sm. (2),(3)). Poetomu vzryvat'sya v nashu epohu sposobny lish' pervichnye ChD s massoi poryadka 1015 g (massa srednei gory). K sozhaleniyu, takie vzryvy do sih por ne nablyudalis'.
temperatura sostavlyaet nichtozhnye doli gradusa, a vremya zhizni ChD namnogo bol'she vremeni sushestvovaniya Vselennoi (sm. (2),(3)). Poetomu vzryvat'sya v nashu epohu sposobny lish' pervichnye ChD s massoi poryadka 1015 g (massa srednei gory). K sozhaleniyu, takie vzryvy do sih por ne nablyudalis'.
Kak ni vpechatlyayushi sledstviya effekta Hokinga, v teoreticheskom plane naibol'shii interes predstavlyaet priroda teplovogo haraktera ChD: imeem li my zdes' delo s chisto sluchainym shodstvom ili zhe po kakim-to prichinam ChD deistvitel'no predstavlyaet soboi goryachee telo? Otvet na etot vopros i sluzhit soderzhaniem ostavsheisya chasti stat'i.
3. Termodinamika chernyh dyr
Posle otkrytiya effekta Hokinga nauchnoe obshestvennoe mnenie sklonyalos' skoree k tomu, chto imeet mesto chisto vneshnyaya analogiya s termodinamicheskimi sootnosheniyami. Ved' ni v samoi postanovke zadachi ob izluchenii ChD, ni v chisto dinamicheskom metode ee resheniya net, kazalos' by, ni maleishego nameka na termodinamiku. Odnako takaya tochka zreniya prosushestvovala nedolgo. Prishlos' vspomnit', chto eshe do otkrytiya Hokinga vyskazyvalos' nemalo soobrazhenii, svidetel'stvuyushih o tesnom perepletenii fiziki ChD i termodinamiki.
Vse nachalos', po-vidimomu, s zadachi, kotoruyu postavil izvestnyi amerikanskii teoretik Dzh. Uiler pered svoim aspirantom Dzh. Bekenshteinom za neskol'ko let do rabot Hokinga. Pust' pervonachal'no imeyutsya ChD i vdali ot nee goryachee telo, obladayushee nekotorym zapasom entropii. Eta velichina, o kotoroi upominaetsya v epigrafe stat'i, predstavlyaet soboi meru togo haosa, kotoryi my svyazyvaem s ponyatiem teploty (o kolichestvennom opredelenii entropii sm. nizhe razdel 5). ChD prityanet k sebe telo, kotoroe v konce koncov uidet pod gorizont sobytii. Togda nablyudatel' stolknetsya s yavnym narusheniem vtorogo nachala termodinamiki, soglasno kotoromu polnaya entropiya zamknutoi sistemy (v dannom sluchae sistemy ChD + telo) ne mozhet umen'shat'sya so vremenem - poryadok v otlichie ot haosa ne mozhet voznikat' sam soboi. Ved' v nachale entropiya sistemy ravnyalas' entropii tela, a v konce ona ischezla, tak kak vnutrennost' ChD nablyudatelyu nedostupna. Na eto hochetsya vozrazit', chto na samom dele entropiya tela ne ischezla, a peredalas' vnutrennei chasti ChD. No etot argument ne bolee chem otgovorka: fizicheskii mir vneshnego nablyudatelya ne vklyuchaet v sebya vnutrennosti ChD, a obshie zakony fiziki dolzhny vypolnyat'sya imenno v etom mire.
Sushestvovali i drugie, bolee formal'nye svidetel'stva togo, chto v fizike ChD, tak skazat', "pahnet" termodinamikoi. Naprimer, kak pokazal sam Hoking, poverhnost' ChD (dlya neskol'kih ChD - summa poverhnostei)
|
|
(4) |
vedet sebya podobno entropii, ne umen'shayas' ni pri kakih estestvennyh processah s uchastiem ChD - pri padenii veshestva v ChD, pri sliyanii dvuh ChD v odnu i t.p. (v etom legko ubedit'sya s pomosh'yu sootnoshenii (1), (4)). Odnako do pory do vremeni takie svidetel'stva vosprinimalis' kak proyavlenie chisto formal'noi analogii.
Po-vidimomu, tol'ko Bekenshtein pochuvstvoval, chto za vsem skazannym stoit glubokaya fizika. Otvergnuv vozmozhnost' narusheniya vtorogo nachala, on dal sleduyushee reshenie zadachi Uilera. Pri padenii tela vnutr' ChD takie ego harakteristiki, kak massa, vrashatel'nyi moment i zaryad, ne ischezayut, a peredayutsya ChD kak celomu, menyaya sootvetstvuyushim obrazom znacheniya ee nablyudaemyh parametrov ![]() (sm. konec razdela 1). Bekenshtein rasshiril spisok takih harakteristik tela, vklyuchiv v nego i entropiyu, odnovremenno vvedya ee i v spisok nablyudaemyh parametrov ChD. Spasenie vtorogo nachala proishodit pri etom potomu, chto padayushee telo menyaet (uvelichivaet) entropiyu samoi ChD na velichinu, ne men'shuyu ishodnoi entropii tela.
(sm. konec razdela 1). Bekenshtein rasshiril spisok takih harakteristik tela, vklyuchiv v nego i entropiyu, odnovremenno vvedya ee i v spisok nablyudaemyh parametrov ChD. Spasenie vtorogo nachala proishodit pri etom potomu, chto padayushee telo menyaet (uvelichivaet) entropiyu samoi ChD na velichinu, ne men'shuyu ishodnoi entropii tela.
No Bekenshtein na etom ne ostanovilsya, vser'ez vosprinyav ChD kak termodinamicheskii ob'ekt. On opredelil temperaturu ChD (ona prakticheski sovpala s rezul'tatom Hokinga, sm. (2)), pridumav osobogo roda mashinu, kotoraya sposobna (myslenno, konechno) prevrashat' teplo v rabotu v pole ChD (grubo govorya, eto zapolnennyi goryachim izlucheniem konteiner na dlinnoi niti, kotoryi posle ego spuska do gorizonta sobytii oporozhnyaetsya, potom podnimaetsya obratno uzhe v oblegchennom vide; vyigrysh v energii pri spuske poetomu ne men'she ee zatrat pri pod'eme, ris. 2).
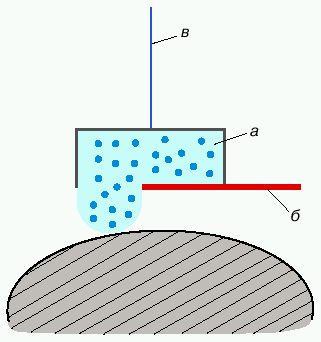 |
| Ris. 2. Teplovaya mashina Bekenshteina: a - konteiner s goryachim izlucheniem, b - zaslonka, v - nit' |
Temperatura ChD opredelyaetsya koefficientom poleznogo deistviya takoi mashiny (teorema Karno). Odnovremenno, ispol'zuya (4) , Bekenshtein nashel i entropiyu ChD, okazavshuyusya proporcional'noi ee poverhnosti.
|
|
(5) |
Etot fakt snimaet pokrov tainstvennosti so skazannogo vyshe o svoistvah poverhnosti ChD, okazyvayushihsya pryamym sledstviem vtorogo nachala termodinamiki.
Opredeliv temperaturu i entropiyu ChD, Bekenshtein, odnako, ne sdelal poslednego shaga - ne predskazal samogo effekta Hokinga, kotoryi po spravedlivosti dolzhen byl by nosit' imya oboih uchenyh.
4. Kollaps tel maloi massy
Vyvodom o neravenstve nulyu temperatury ChD (i tem samym o sushestvovanii effekta Hokinga) rezul'taty termodinamiki ChD daleko ne ogranichivayutsya. Eta teoriya, kak i lyuboi drugoi razdel termodinamiki, pozvolyaet delat' obshie i dostatochno sil'nye utverzhdeniya bez provedeniya konkretnyh mikroskopicheskih raschetov. Eshe odin primer takogo roda privoditsya v etom razdele.
Vyshe uzhe govorilos', chto kollaps mogut ispytyvat' lish' tela s massoi, prevyshayushei primerno ![]() . V 1962 godu sovetskii teoretik Ya.B. Zel'dovich pokazal, chto takaya granica otnositsya lish' k bystromu kollapsu. V deistvitel'nosti neuderzhimo szhimat'sya, hotya i chrezvychaino medlenno, sposobno telo proizvol'no maloi massy - sostoyanie ChD energeticheski predpochtitel'no pri lyubom znachenii M.
. V 1962 godu sovetskii teoretik Ya.B. Zel'dovich pokazal, chto takaya granica otnositsya lish' k bystromu kollapsu. V deistvitel'nosti neuderzhimo szhimat'sya, hotya i chrezvychaino medlenno, sposobno telo proizvol'no maloi massy - sostoyanie ChD energeticheski predpochtitel'no pri lyubom znachenii M.
Termodinamika ChD vnosit sushestvennye korrektivy v etot vyvod. Primenim k processu kollapsa vtoroe nachalo termodinamiki, trebuyushee, chtoby entropiya ishodnogo sostoyaniya byla ne bol'she entropii voznikayushego iz nego sostoyaniya ChD. Pervuyu iz etih velichin mozhno ocenit', schitaya, chto na kazhduyu stepen' svobody klassicheskoi sistemy chastic prihoditsya entropiya poryadka postoyannoi Bol'cmana
|
|
(6) |
gde m = 1,6 ![]() 10-24 g - massa nuklona. Vtoraya velichina daetsya formuloi (5) . Otsyuda prezhde vsego vidno, chto process kollapsa s obrazovaniem zvezdnoi ChD sil'no neobratim: entropiya v itoge takogo processa vozrastaet pochti na 20 poryadkov dlya
10-24 g - massa nuklona. Vtoraya velichina daetsya formuloi (5) . Otsyuda prezhde vsego vidno, chto process kollapsa s obrazovaniem zvezdnoi ChD sil'no neobratim: entropiya v itoge takogo processa vozrastaet pochti na 20 poryadkov dlya ![]() .
.
Budem teper' umen'shat' massu M. Pri etom, kak vidno iz formul (5), (6),![]() , no ostaetsya otlichnoi ot nulya. Podcherknem, chto privedennye rassuzhdeniya otnosilis' lish' k kollapsu izolirovannogo tela i nikoim obrazom neprilozhimy k pervichnym ChD (sm. razdel 1).
, no ostaetsya otlichnoi ot nulya. Podcherknem, chto privedennye rassuzhdeniya otnosilis' lish' k kollapsu izolirovannogo tela i nikoim obrazom neprilozhimy k pervichnym ChD (sm. razdel 1).
5. Termodinamika i informaciya
Sushestvovanie oblasti, informaciya iz kotoroi ne dohodit do nablyudatelya, imeet dlya termodinamiki ChD principial'noe znachenie. Eto vidno uzhe iz formulirovki zadachi Uilera, opisannoi v razdele 3, razdele 3, kotoraya posluzhila otpravnym punktom argumentacii Bekenshteina. V bolee obshem plane eto yasno iz sleduyushih kvantovomehanicheskih soobrazhenii. Goryachaya ChD, kak i lyuboe goryachee telo, dolzhna opisyvat'sya ne volnovoi funkciei, a osoboi velichinoi - matricei plotnosti, kotoraya osushestvlyaet nepolnoe opisanie sistemy. Takaya nepolnota v sluchae obychnogo goryachego tela svyazana s nevozmozhnost'yu detal'nogo opisaniya sostavlyayushih ego chastic, v sluchae ChD kak dinamicheskoi sistemy - s sushestvovaniem ukazannoi vyshe oblasti.
Sushestvuet dostoinaya osobogo vnimaniya vozmozhnost' pryamogo perehoda ot utverzhdeniya "nablyudatel' ne imeet informacii o vnutrennei chasti ChD" k utverzhdeniyu "ChD obladaet zapasom entropii, a znachit, i otlichnoi ot nulya temperaturoi". Eta vozmozhnost' opiraetsya na sformulirovannyi amerikanskim fizikom L. Scillardom osobyi informacionnyi podhod k termodinamike, kotoryi voshodit k klassikam teorii teploty i razvivalsya mnogimi fizikami i matematikami. Takoi podhod po suti svoditsya k ustanovleniyu pryamoi svyazi velichiny entropii sistemy s nedostatkom informacii o ee vnutrennei strukture. Srazu zhe podcherknem, chto rech' idet ob ob'ektivnom, principial'no nevospolnimom nedostatke informacii, a ne prosto ob otkaze ot vozmozhnoi v principe registracii harakteristik sistemy.
Ideyu informacionnogo podhoda sformuliruem snachala na primere obychnoi termodinamiki, tochnee govorya, na primere perehoda dinamicheskoi sistemy v sostoyanie termodinamicheskogo ravnovesiya. Budem opirat'sya na real'nyi primer - metod polucheniya vysokotemperaturnoi plazmy putem inzhekcii v special'nuyu kameru sgustka uskorennyh chastic s ego posleduyushei termalizaciei. Pervonachal'nyi sgustok - dlya opredelennosti monohromaticheskii i polyarizovannyi - predstavlyaet soboi dinamicheskuyu sistemu, opisyvaemuyu volnovoi funkciei. V processe nelineinogo vzaimodeistviya chastic sgustka v kamere i razvitiya sootvetstvuyushih neustoichivostei sistema chastic haotizuetsya i perehodit v termodinamicheski ravnovesnoe sostoyanie, opisyvaemoe matricei plotnosti, prichem sootvetstvuyushaya temperatura opredelyaetsya pervonachal'noi energiei sgustka. V itoge sistema "zabyvaet" svoe nachal'noe sostoyanie, harakterizuyas' sushestvenno men'shim chislom parametrov (energiya ili temperatura, davlenie ili ob'em i t.p.), chem polnoe chislo ee stepenei svobody. Sushestvenno, chto kazhdomu naboru takih parametrov otvechaet ogromnoe chislo N razlichnyh mikrosostoyanii sistemy - kompleksii po terminologii Bol'cmana, kotorye realizuyut etot nabor i kotorye my v principe ne mozhem razlichat'. Ravnoveroyatnost' razlichnyh kompleksii, nevozmozhnost' predpochest' odnu iz nih drugoi i est' tochnyi i naibolee obshii smysl ponyatiya "haos".
Chislo kompleksii N opredelyaet po sushestvu stepen' nepolnoty nashih svedenii o mikrostrukture sistemy pri zadannom nabore ukazannyh makroskopicheskih parametrov. Bolee udobnoi meroi takoi nepolnoty informacii o sisteme sluzhit uzhe mnogokratno upomyanutaya vyshe entropiya sistemy, opredelyaemaya sootnosheniem
|
|
(7) |
i izmeryaemaya v edinicah postoyannoi Bol'cmana (sm. formulu (5)). My podoshli, takim obrazom, k informacionnomu tolkovaniyu entropii.
Chtoby dat' takomu tolkovaniyu kolichestvennuyu formulirovku, vvedem sleduyushee prosteishee opredelenie izmeneniya kolichestva informacii ![]() v rezul'tate nekotorogo processa. Pust' do ego nachala imelos' P ravnoveroyatnyh otvetov na nekotoryi vopros o rassmatrivaemoi sisteme, ni odin iz kotoryh nel'zya predpochest' drugomu. Pust' po okonchanii processa chislo takih otvetov stalo p. Togda izmenenie informacii o sisteme imeet vid
v rezul'tate nekotorogo processa. Pust' do ego nachala imelos' P ravnoveroyatnyh otvetov na nekotoryi vopros o rassmatrivaemoi sisteme, ni odin iz kotoryh nel'zya predpochest' drugomu. Pust' po okonchanii processa chislo takih otvetov stalo p. Togda izmenenie informacii o sisteme imeet vid
![]() .
.
Esli P > p, to imeetsya prirost informacii ![]() > 0 - nashi svedeniya o sisteme stali bolee opredelennymi, a v obratnom sluchae - ee ubyl'.
> 0 - nashi svedeniya o sisteme stali bolee opredelennymi, a v obratnom sluchae - ee ubyl'.
Prilozhim takoe opredelenie k rassmotrennomu vyshe processu perehoda sistemy v termodinamicheski ravnovesnoe sostoyanie. Vnachale ona byla chisto dinamicheskoi, ee entropiya ravnyalas' nulyu, i my znali edinstvennyi otvet na vopros o ee mikrosostoyanii: P = 1. V konce entropiya sistemy uvelichilas' na velichinu ![]() , a chislo otvetov na postavlennyi vopros vyroslo do p = N. Poetomu ubyl' informacii posle termalizacii ravna
, a chislo otvetov na postavlennyi vopros vyroslo do p = N. Poetomu ubyl' informacii posle termalizacii ravna ![]() , i my prishli k osnovnomu sootnosheniyu informacionnogo podhoda (sm. (7))
, i my prishli k osnovnomu sootnosheniyu informacionnogo podhoda (sm. (7))
|
|
(8) |
to est' umen'shenie kolichestva informacii o sisteme ravno prirostu ee entropii i obratno. Vazhno, chto pri vyvode (8) ne ispol'zovalsya nikakoi konkretnyi mehanizm poteri informacii, chto pobuzhdaet schitat' eto sootnoshenie universal'nym.
Proillyustriruem sootnoshenie (8) prostym primerom neobratimogo rasshireniya na ves' ob'em gaza, pervonachal'no sosredotochennogo v polovine ob'ema (ris. 3).
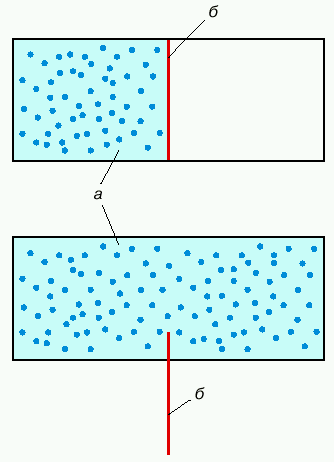 |
| Ris. 3. Rasshirenie gaza v udvoennyi ob'em. a) - gaz, b) - zaslonka |
Ochevidno, chto chislo ravnoveroyatnyh otvetov na vopros o poperechnoi po otnosheniyu k zaslonke koordinate molekuly gaza uvelichivaetsya posle podnyatiya zaslonki vdvoe. Sootvetstvuyushaya ubyl' informacii ravna kln 2, chto v sootvetstvii s (8) tochno ravno izvestnomu iz termodinamiki vyrazheniyu dlya prihodyashegosya na odnu molekulu prirosta entropii v rassmatrivaemom processe.
Vazhno podcherknut', chto iz sootnosheniya (8) nikoim obrazom ne sleduet vozmozhnost' narushit' vtoroe nachalo termodinamiki, to est' umen'shit' entropiyu zamknutoi sistemy putem uvelicheniya ob'ema informacii o nei. Delo v tom, chto za poluchenie informacii nado platit' opredelennuyu cenu, v tom chisle entropiinuyu, poskol'ku sam etot process neobratim. Tak, naprimer, pri opredelenii koordinaty molekuly putem ee osvesheniya pridetsya schitat'sya s tem, chto rasseyannyi molekuloi svet v konce koncov dissipiruet, poglotitsya sistemoi, povysiv ee entropiyu na velichinu, ne men'shuyu vyigrysha za schet sootnosheniya (8). Samoe bol'shee, chego mozhno dostich', - eto pereraspredelit' entropiyu (stepen' haotichnosti) s odnih stepenei svobody na drugie. Imenno k etomu i svoditsya rabota tehnicheskih ustroistv, uporyadochivayushih sistemu po nekotorym parametram, - regulyatorov, kotorye obyazatel'no imeyut special'nyi organ (datchik), schityvayushii informaciyu o reguliruemoi velichine.
Pereidem, nakonec, k izlozheniyu informacionnogo podhoda primenitel'no k processu obrazovaniya ChD. Situaciya zdes' ochen' blizka k rassmotrennomu primeru termalizacii sgustka (ot nesushestvennoi raznicy - vozmozhnosti nenulevoi temperatury u predshestvennika ChD - mozhno otvlech'sya). Kak bylo otmecheno v konce razdela 1, i v sluchae ChD nam byl dostupen ogromnyi ob'em informacii o mikrosostoyanii ee predshestvennika, "zabytyi" v processe obrazovaniya ChD, kotoraya pomnit lish' maloe chislo nablyudaemyh parametrov. Poetomu primenitel'no k obrazovaniyu ChD mozhno povtorit' pochti vse skazannoe vyshe. Vo vsyakom sluchae sam fakt obladaniya ChD otlichnoi ot nulya entropiei nuzhno schitat' estestvennym i neizbezhnym.
Ostaetsya, odnako, kolichestvennaya problema dokazatel'stva sovpadeniya informacionnoi (sm. (7) ili (8)) i termodinamicheskoi (sm. (6)) formul dlya entropii. Dlya etogo nuzhno prezhde vsego vyyavit' te mikrosostoyaniya, informacii o kotoryh lishen vneshnii nablyudatel'. Uzhe iz fakta sil'noi neobratimosti processa obrazovaniya zvezdnoi ChD (sm. razdel 4) sleduet, chto oni ne svyazany so stepenyami svobody predshestvennika ChD. Etot vopros okazalsya daleko ne prostym, poetomu reshenie obsuzhdaemoi problemy zatyanulos' na dolgie gody. Takoe reshenie bylo predlozheno lish' v samoe poslednee vremya. Issledovaniya sotrudnikov Fizicheskogo instituta im. P.N. Lebedeva RAN, rossiiskih teoretikov I.D.Novikova i V.P.Frolova pokazali, chto mikrosostoyaniya, igrayushie rol' kompleksii Bol'cmana (sm. razdel 5), svyazany s komponentami par, kotorye rozhdeny okolo gorizonta sobytii (ris. 1), padayushimi vnutr' ChD. Podschet ih vklada v entropiyu ChD vedet k formule (5).
6. Nekotorye drugie primery
Utverzhdenie ob universal'noi svyazi (8) izmenenii entropii i informacii podkrepim dvumya ukazannymi kanadskim fizikom U. Unru primerami, ne otnosyashimisya k fizike ChD. Pervyi iz nih mozhno schitat' gazodinamicheskim analogom ChD. Rassmotrim ob'em gaza vysokogo davleniya, okruzhennyi zvukopogloshayushei stenkoi s otverstiem, skvoz' kotoroe vyryvaetsya gaz so sverhzvukovoi skorost'yu, priobretaemoi, naprimer, pri protekanii cherez soplo Lavalya (ris. 4). V ramkah gazodinamiki (ot opticheskih yavlenii my otvlekaemsya) srez sopla mozhno schitat' gorizontom sobytii: nikakoi zvukovoi signal ne mozhet proniknut' snaruzhi vnutr' ob'ema. Soglasno informacionnomu podhodu, nasha sistema dolzhna obladat' zapasom entropii. I deistvitel'no, kvantovyi raschet zvukovogo polya okolo otverstiya pokazyvaet, chto ono sluzhit istochnikom fononov, nahodyashihsya v sostoyanii termodinamicheskogo ravnovesiya s nekotoroi otlichnoi ot nulya temperaturoi.
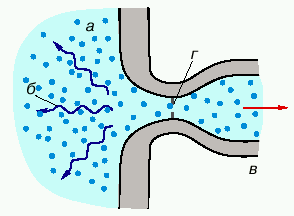 |
| Ris. 4. Gazodinamicheskoe ustroistvo Unru: a - gaz, b - zvuk, v - soplo Lavalya, g - ego sverhzvukovoi srez, igrayushii rol' gorizonta sobytii |
Vtoroi primer bolee slozhen. Horosho izvestno, chto yavleniya v pole tyagoteniya i uskorennoi sisteme otscheta imeyut ochen' blizkuyu i glubokuyu analogiyu, kotoraya podskazala Einshteinu put' k sozdaniyu obshei teorii otnositel'nosti. Proyavleniem takoi analogii sluzhit, naprimer, nevesomost' v orbital'nom polete: tyagotenie i centrobezhnaya sila tochno kompensiruyut drug druga. Poetomu mozhno ozhidat', chto silu tyagoteniya kak prichinu effekta Hokinga mozhno zamenit' perehodom k uskorennoi sisteme otscheta, dvizhusheisya s uskoreniem a. I v samom dele raschet pokazyvaet, chto ravnomerno uskorennyi v vakuume nablyudatel' uvidit teplovoe izluchenie, otvechayushee temperature
![]() .
.
Dlya poyasneniya otmetim bez dokazatel'stva, chto i v rassmatrivaemom sluchae imeetsya gorizont sobytii: sushestvuet oblast' prostranstva-vremeni, dlya kotoroi ispushennyi iz nee svet nikogda ne dogonit uskorennogo nablyudatelya. K tomu zhe v vakuume vsegda est' fizicheskie korotkozhivushie polya (nulevye kolebaniya), kotorye ne registriruyutsya obychnym, dvizhushimsya inercial'no priborom, nastroennym na eti kolebaniya kak na "nul'" (nachalo otscheta). Tot zhe pribor, dvizhushiisya uskorenno, zaregistriruet takie kolebaniya kak teplovoe izluchenie.
7. Zaklyuchenie
Sushestvovanie ChD, predskazannyh v ih sovremennom ponimanii obshei teoriei otnositel'nosti, s bol'shoi dolei veroyatnosti uzhe podtverzhdeno nablyudeniyami (sm. razdel 1). Esli eta veroyatnost' prevratitsya v polnuyu uverennost', to uzhe rol' ChD kak istochnikov aktivnosti yader galaktik i kvazarov pozvolit schitat' ih vazhneishim elementom mirozdaniya. Ne isklyucheno, chto eshe ne otkrytye pervichnye ChD, esli oni deistvitel'no sushestvuyut, imeyut kuda bol'shuyu znachimost' dlya kosmofiziki, chem eto kazhetsya segodnya.
Odnako uzhe seichas mozhno govorit' i o sovsem inoi, obshefizicheskoi roli ChD, obogativshih nashi obshie predstavleniya o neorganicheskom mire. Poyavlenie ChD kak produkta teoreticheskoi mysli podnyalo na novyi uroven' ponimanie teploty. S XVIII-XIX vekov - vremeni pobedy kineticheskoi teorii nad teoriei teploroda - nauka znala edinstvennyi mehanizm poyavleniya tepla - haotizaciyu dvizheniya chastic, obladayushih zapasom kineticheskoi energii. Takoi mehanizm proyavlyaetsya i pri trenii dvuh kuskov dereva, s pomosh'yu chego nashi predki dobyvali ogon', i pri himicheskih i yadernyh reakciyah. S naibolee obshei, informacionnoi tochki zreniya poyavlenie tepla vo vseh takih sluchayah otvechaet utrate mikroskopicheskoi informacii o sostoyanii chastic goryachego tela.
Fizika ChD ukazala novyi mehanizm vozniknoveniya tepla, kogda informaciya o vnutrennem sostoyanii ChD otsekaetsya ot nablyudatelya moshnymi silami tyagoteniya (a sam etot ob'ekt mozhet byt' upodoblen "chernomu yashiku", kak v kibernetike nazyvayut ustroistvo s neizvestnoi vnutrennei strukturoi). Etot novyi mehanizm deistvuet po sheme
chernaya dyra ![]() chernyi yashik
chernyi yashik ![]() chernoe telo
chernoe telo
i takzhe imeet delo s haosom, kotoromu otvechaet ravnoveroyatnost' s tochki zreniya vneshnego nablyudatelya razlichnyh mikrosostoyanii vnutrennei chasti ChD, sovmestimyh s zadannymi znacheniyami massy, momenta i zaryada (sm. razdel 5, konec tret'ego abzaca).
Skazannomu tochno sootvetstvuyut slova velikogo russkogo pisatelya, fizika po obrazovaniyu, vzyatye epigrafom k stat'e (hotya sam on, konechno, vkladyval v nih sovsem inoi, obshestvenno-politicheskii smysl).
Literatura
| [1] | Novikov I.D., Frolov V.P. Fizika chernyh dyr. M.: Nauka, 1986. |
| [2] | Kirzhnic D.A., Frolov V.P. // Priroda. 1981. No 11. S. 2. |
| [3] | Kirzhnic D.A., Frolov V.P. // Proshloe i budushee Vselennoi. M.: Nauka, 1986. S. 61. |
| [4] | Brillyuen L. Nauka i teoriya informacii. M.: Fizmatgiz, 1960. |
| [5] | Hawking S. // Sci. Amer. 1977. Vol. 236, No 1. P. 34. |
| [6] | Bekenstein J. // Phys. Today. 1980. No 1. P. 24. |
|
Publikacii s klyuchevymi slovami:
chernye dyry - temperatura chernyh dyr - effekt Hokinga - isparenie chernyh dyr - termodinamika chernyh dyr
Publikacii so slovami: chernye dyry - temperatura chernyh dyr - effekt Hokinga - isparenie chernyh dyr - termodinamika chernyh dyr | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |