Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Solnechnyi veter

M.I.PUDOVKIN

Sankt-Peterburgskii gosudarstvennyi universitet

Privoditsya obzor sovremennyh predstavlenii o mehanizme formirovaniya solnechnogo vetra, podrobno izlagaetsya teoriya Parkera, obsuzhdaetsya rol' magnito-gidrodinamicheskih voln v nagreve i uskorenii solnechnogo vetra. Rassmatrivayutsya osobennosti vysokoskorostnyh potokov v solnechnom vetre i ih vozmozhnye istochniki na Solnce.

Vvedenie

Kak pokazyvayut nablyudeniya, vypolnennye na bortu sputnikov Zemli i drugih kosmicheskih apparatov s vysokim apogeem orbity, mezhplanetnoe prostranstvo zapolneno chrezvychaino aktivnoi sredoi - plazmoi solnechnogo vetra. Solnechnyi veter zarozhdaetsya v verhnih sloyah atmosfery Solnca, i ego osnovnye parametry opredelyayutsya sootvetstvuyushimi parametrami solnechnoi atmosfery. Odnako svyaz' mezhdu fizicheskimi harakteristikami solnechnogo vetra vblizi orbity Zemli i fizicheskimi yavleniyami v atmosfere Solnca okazyvaetsya chrezvychaino slozhnoi i, krome togo, menyaetsya v zavisimosti ot urovnya solnechnoi aktivnosti i konkretnoi situacii na Solnce. Poetomu dlya prostoty opisaniya predpolagaetsya, chto nablyudaemyi vblizi orbity Zemli solnechnyi veter sostoit iz treh v pervom priblizhenii nezavisimyh komponent [1]:

  1. spokoinyi solnechnyi veter - postoyanno sushestvuyushii potok solnechnoi plazmy, zapolnyayushii vse mezhplanetnoe prostranstvo vplot' do granic geliosfery (50-200 a.e.);

  2. kvazistacionarnye vysokoskorostnye potoki solnechnoi plazmy, otvetstvennye za rekurrentnye geomagnitnye vozmusheniya;

  3. sporadicheskie vysokoskorostnye potoki - otnositel'no kratkovremennye, chrezvychaino neodnorodnye i slozhnye po strukture obrazovaniya, otvetstvennye za sporadicheskie magnitosfernye vozmusheniya.

Sleduya etoi sheme, rassmotrim morfologicheskie harakteristiki i mehanizm formirovaniya ukazannyh komponent solnechnogo vetra.

Spokoinyi solnechnyi veter

Soglasno sovremennym predstavleniyam, energiya v nedrah Solnca vyrabatyvaetsya v hode processov yadernogo sinteza:

1H + 1H $\rightarrow$ 2D + e+ + $\nu$ + 1,44 MeV,

2D + 1H $\rightarrow$ 3He + $\gamma$ + 5,49 MeV, (1)

3He + 3He $\rightarrow$ 4He + 1H + 1H + 12,85 MeV,

gde e+ oboznachaet pozitron, $\nu$ - neitrino i $\gamma$ - $\gamma$ -kvant. V rezul'tate perechislennyh processov 1,0078 g vodoroda perehodit v 1,0000 g geliya, a ostavshayasya massa prevrashaetsya v kineticheskuyu energiyu chastic i energiyu radiacii. Skorost' vydeleniya energii v hode reakcii proton-protonnogo cikla opredelyaetsya vyrazheniem

$$\varepsilon_{pp}=2,5\cdot 10^{6}\rho X^{2}(\frac{10^{6}}{T})^{2/3}\exp[-33,8(\frac{10^{6}}{T})^{1/3}]~\mbox{erg/(g}\cdot\mbox{s)}\,,$$ (2)

gde $\rho$ - plotnost' solnechnogo veshestva, X - otnositel'noe soderzhanie v nem yader vodoroda i T - temperatura. Prinimaya vo vnimanie, chto kak plotnost' veshestva, tak i ego temperatura vozrastayut k centru Solnca, mozhno pokazat', chto okolo 99% solnechnoi energii generiruetsya v yadre Solnca s radiusom $R_{c} = 0,25R_{\odot}$ .

Izvestno, chto v zvezdah tipa Solnca teploprovodnost' igraet neznachitel'nuyu rol', tak chto proizvedennaya v nedrah Solnca energiya peredaetsya k ego poverhnosti v osnovnom putem radiacionnogo perenosa, to est' v rezul'tate ee poglosheniya i posleduyushego pereizlucheniya[2].

Odnako radiacionnyi perenos solnechnoi energii stanovitsya maloeffektivnym v verhnih sloyah Solnca. Delo v tom, chto po mere umen'sheniya temperatury solnechnogo veshestva stepen' ego ionizacii umen'shaetsya i prisutstvie v nem neitral'nyh atomov vodoroda zametno snizhaet ego prozrachnost'. Eto, v svoyu ochered', privodit k eshe bolee bystromu umen'sheniyu temperatury Solnca s rasstoyaniem ot centra, vsledstvie chego lyuboi elementarnyi ob'em solnechnogo veshestva, vsplyvayushii iz nedr Solnca, obladaet bol'shei temperaturoi i men'shei plotnost'yu, chem okruzhayushaya plazma, chto privodit k razvitiyu tak nazyvaemoi konvektivnoi neustoichivosti. Usloviya ee vozbuzhdeniya uverenno vypolnyayutsya v poverhnostnyh sloyah Solnca $r > 0,86R_{\odot}$[2], gde energiya perenositsya glavnym obrazom v forme teplovoi energii plazmy, zaklyuchennoi v elementah veshestva, podnimayushihsya iz nedr Solnca.

Razvitie intensivnoi turbulentnosti v poverhnostnyh sloyah Solnca ne tol'ko obespechivaet perenos energii k ego poverhnosti, no i privodit k razvitiyu yavlenii, igrayushih klyuchevuyu rol' v solnechno-zemnoi fizike. Prezhde vsego razvitie konvektivnoi turbulentnosti v plazme soprovozhdaetsya generaciei intensivnyh magnitozvukovyh voln. Rasprostranyayas' v atmosfere Solnca, gde plotnost' plazmy bystro umen'shaetsya s vysotoi, zvukovye volny transformiruyutsya v udarnye. Oni effektivno pogloshayutsya veshestvom, v rezul'tate chego temperatura poslednego uvelichivaetsya, dostigaya velichiny (1) - (3) $\cdot$ 106 K v solnechnoi korone. Pri etom znachitel'naya chast' protonov v korone Solnca ne mozhet uderzhivat'sya ego gravitacionnym polem, chto privodit k nepreryvnomu rasshireniyu korony v kosmicheskoe prostranstvo, to est' k generacii solnechnogo vetra.

V sovremennoi forme model' solnechnogo vetra byla razrabotana E. Parkerom [3]. Kratkoe izlozhenie etoi modeli predstavleno nizhe.

V stacionarnom sfericheski-simmetrichnom sluchae uravneniya gazodinamiki mogut byt' zapisany v sleduyushei forme:

Uravnenie dvizheniya

$$\upsilon (r)\frac{d\upsilon (r)}{dr} = -\frac{1}{\rho(r)} \frac{dp(r)}{dr} + \frac{M_{\odot}G}{r^{2}}\,,$$ (3)

gde $\upsilon (r)$ - skorost' solnechnogo vetra, $\rho (r)$ i $p(r)$ - ego plotnost' i davlenie; $M_{\odot}$ - massa Solnca i G - gravitacionnaya postoyannaya;

Uravnenie nerazryvnosti potoka veshestva

$$\rho(r)\upsilon(r)A(r) =\rho_{0}\upsilon_{0}A_{0}\,,$$ (4)

gde A(r) = A0(r / r0)2 - ploshad' poperechnogo secheniya potokovoi trubki, indeksom 0 otmecheny znacheniya peremennyh na nekotorom ishodnom rasstoyanii r0 ot centra Solnca;

Uravnenie gazovogo sostoyaniya

$$p(r)=p_{0}\left(\frac{\rho (r)}{\rho_{0}}\right)^{\alpha}\,,$$ (5)

gde $\alpha$ - pokazatel' politropy, $1\leq \alpha \leq 5/3\,,$ otlichnyi ot 5/3 (pokazatel' adiabaty) pri nalichii dopolnitel'nyh istochnikov energii v solnechnom vetre, o nih rech' poidet nizhe.

Podstavlyaya ravenstva (4) i (5) v uravnenie (3) i integriruya poslednee po r, poluchaem uravnenie Bernulli (pri $\alpha \neq 1$) v forme

$$\frac{1}{2}\upsilon^{2}-\frac{GM_{\odot}}{r}+\frac{\alpha}{\alpha -1}\frac{p_{0}}{\rho_{0}}\frac{\upsilon_{0}A_{0}}{\upsilon A}=\frac{1}{2}\upsilon^{2}_{0}-\frac{GM_{\odot}}{r_{0}}+\frac{\alpha}{\alpha-1}\frac{p_{0}}{\rho_{0}}$$ (6)

Perehodya k bezrazmernym peremennym

$$\zeta=\frac{r}{r_0}, \quad u^{2}=\frac{1}{2}\frac{\rho_0}{r_0}\upsilon^2, \quad H=\frac{GM_{\odot}\rho_0}{r_{0}p}\,,$$ (7)

perepishem uravnenie (6) v vide

$$u^2 + \frac{\alpha}{\alpha-1}\left(\frac{u_o}{u\zeta^2}\right)^{\alpha-1}-\frac{H}{\zeta}=u^{2}_{0} + \frac{\alpha}{\alpha-1}-H\equiv u^{2}_{1}\,,$$ (8)

gde $u_1$ - konstanta integrirovaniya, zavisyashaya ot granichnyh uslovii na poverhnosti $r = r_0$ .

Uravneniya (6) ili (8) opredelyayut izmenenie skorosti solnechnogo vetra s rasstoyaniem ot Solnca. Reshenie etih uravnenii neodnokratno rassmatrivalos' v literature [1],[3],[4], i my lish' kratko obsudim poluchennye rezul'taty. Uravneniya (6) ili (8) ne imeyut tochnogo analiticheskogo resheniya, poetomu Parker issleduet asimptotiku resheniya na bol'shih ($\zeta \gg 1$) i malyh ($\zeta \ll 1$) rasstoyaniyah ot Solnca.

Bol'shie rasstoyaniya

Ochevidno, chto pri $\zeta \rightarrow \infty \qquad u(\zeta)$ mozhet libo neogranichenno vozrastat', libo stremit'sya k kakoi-libo postoyannoi velichine ili k nulyu. Netrudno videt', chto $u \rightarrow \infty $ ne udovletvoryaet uravneniyu (8). Deistvitel'no, pervyi chlen v levoi chasti uravneniya neogranichenno vozrastaet, vtoroi i tretii chleny stremyatsya k nulyu, togda kak v pravoi chasti (8) $u^{2}_{1}$= const.

Variant $u|_{\zeta \rightarrow \infty}$ = const okazyvaetsya vozmozhnym. V etom sluchae

$$\left.u\right|_{\zeta \rightarrow \infty}\longrightarrow u_1\,.$$ (9a)

Reshenie $u|_{\zeta \rightarrow \infty}\rightarrow 0$ takzhe udovletvoryaet uravneniyu (8). V etom sluchae pervyi i tretii chleny v levoi chasti uravneniya (9) stremyatsya k nulyu i

$$u|_{\zeta \rightarrow \infty}\longrightarrow \frac{u_{0}}{\zeta^{2}}\left(\frac{\alpha}{\alpha-1}\frac{1}{u^2}\right)^{\frac{1}{\alpha-1}}\,.$$ (9b)

Takim obrazom, reshenie uravneniya (8) na bol'shih rasstoyaniyah imeet dve vetvi: verhnyuyu ($u \rightarrow u_1$) i nizhnyuyu ($u \rightarrow 0$). Dlya togo chtoby vybrat' reshenie, priemlemoe s fizicheskoi tochki zreniya, vychislim plotnost' plazmy, sootvetstvuyushuyu etim resheniyam.

Iz ravenstva (4) sleduet

$$\rho (r)=\rho_{0}\frac{1}{\zeta^2}\frac{u_0}{u}\,.$$ (10)

Podstavlyaya v (10) velichinu $u$ iz (9a), (9b), nahodim

$$ \left.u\right|_{\zeta \rightarrow \infty} \rightarrow \left\{ % \begin{array}{ll} 0 & \mbox{--- verhnyaya vetv',} \\ \rho_0\left[\frac{(\alpha-1)u^2_1}{\alpha}\right]^{\frac{1}{\alpha-1}} & \mbox{--- nizhnyaya vetv'.} \\ \end{array} % \right. $$ (11)

Iz ravenstv (11) vidno, chto v sluchae, kogda $u(\zeta)$ sootvetstvuet nizhnei vetvi resheniya, plotnost' plazmy pri $u\rightarrow \infty$ stremitsya k konechnoi i otnositel'no bol'shoi velichine, chto protivorechit eksperimental'nym dannym. V to zhe vremya verhnyaya vetv' resheniya sootvetstvuet $\rho |_{\zeta\rightarrow\infty} \rightarrow 0$, chto udovletvoryaet usloviyam modeli. Takim obrazom, na bol'shih rasstoyaniyah ot Solnca fizicheskii smysl imeet lish' verhnyaya vetv' resheniya uravneniya Parkera.

Malye rasstoyaniya (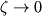$\zeta\rightarrow0$)

Pri $\zeta\rightarrow0$ tretii chlen v levoi chasti ravenstva (8) neogranichenno vozrastaet. Poskol'ku v pravoi chasti uravneniya postoyannaya velichina, eto oznachaet, chto neogranichennoe vozrastanie $(H/\zeta)_{\zeta\rightarrow 0}$ dolzhno byt' skompensirovano odnim iz pervyh dvuh chlenov v levoi chasti (8), to est' opyat' imeyut mesto dve vetvi resheniya:

$$ \left.u\right|_{\zeta \rightarrow 0} \rightarrow \left\{ % \begin{array}{ll} \left(\frac{H}{\zeta}\right)^{1/2} \rightarrow \infty & \mbox{--- verhnyaya vetv',} \\ u_0\left[\frac{\alpha}{\alpha-1}\,\frac{1}{H}\right]^{\frac{1}{\alpha-1}} \zeta^{\frac{1}{\alpha-1}-2} & \mbox{--- nizhnyaya vetv'.} \\ \end{array} % \right. $$ (12)

Pervoe reshenie, sootvetstvuyushee neogranichennomu vozrastaniyu skorosti solnechnogo vetra pri $\zeta \rightarrow 0$, fizicheski nepriemlemo. Vtoroe reshenie daet razumnyi rezul'tat $u|_{\zeta \rightarrow} \rightarrow 0$ pri znacheniyah pokazatelya politropy, opredelyaemyh neravenstvom $1/(\alpha - 1) - 2 > 0$, to est' $\alpha < 3/2$.

Takim obrazom, stacionarnoe reshenie korony okazyvaetsya vozmozhnym lish' v tom sluchae, esli pokazatel' politropy a men'she adiabaticheskogo ($\alpha$ = 5/3), to est' esli imeet mesto nepreryvnyi pritok energii v koronu i solnechnyi veter. V pervonachal'noi modeli Parkera predpolagalos', chto neobhodimyi pritok energii obespechivaetsya vysokoi teploprovodnost'yu solnechnoi plazmy. Odnako, kak budet pokazano nizhe, odnogo lish' potoka teplovoi energii nedostatochno dlya uskoreniya solnechnogo vetra, i trebuyutsya dopolnitel'nye istochniki energii.

Itak, my vidim, chto fizicheski razumnym granichnym usloviyam pri bol'shih $\zeta$ udovletvoryaet verhnyaya vetv' resheniya uravneniya Parkera, a pri malyh $\zeta$ - nizhnyaya. Srashivanie etih dvuh vetvei resheniya zavisit ot povedeniya resheniya v okrestnostyah nekotoroi kriticheskoi tochki, polozhenie kotoroi na ploskosti $(\zeta,u)$ opredelyaetsya sleduyushim obrazom.

Prodifferenciruem uravnenie (8) po $\zeta$:

$$\left( 2u - \frac{\alpha u^{\alpha-1}_{0}}{u^{\alpha}\zeta^{2(\alpha -1)}} \right) \frac{du}{d\zeta}=\frac{2\alpha u^{\alpha -1}_{0}}{u^{\alpha-1}\zeta^{2(\alpha -1)+1}}-\frac{H}{\zeta^2}\,.$$ (13)

Opredelim kriticheskuyu tochku ($\zeta_{c}, u_{c}$) kak tochku, gde pravaya chast' uravneniya (13) i koefficient pri $du/d\zeta$ v levoi chasti uravneniya odnovremenno ravny nulyu. Togda

$$u^{2}_{c}\zeta_{c}=\frac{H}{4}\,, \qquad \zeta_{c}=\left( \frac{H}{4} \right)^{\frac{\alpha +1}{5 - 3\alpha}} \left( \frac{2}{\alpha u^{\alpha -1}_{0}} \right) ^{\frac{2}{5 - 3\alpha}}\,.$$ (14)

Topologiya resheniya uravneniya (8) v okrestnostyah kriticheskoi tochki pokazana na ris. 1. Reshenie predstavlyaet soboi semeistvo giperbol. Pri etom sushestvuet lish' odno reshenie, udovletvoryayushee granichnym usloviyam kak na bol'shih, tak i na malyh rasstoyaniyah ot Solnca. Etomu resheniyu sootvetstvuet krivaya, prohodyashaya cherez kriticheskuyu tochku (kriticheskoe reshenie).

Ris. 1. Semeistvo krivyh resheniya uravneniya Parkera v okrestnosti kriticheskoi tochki.

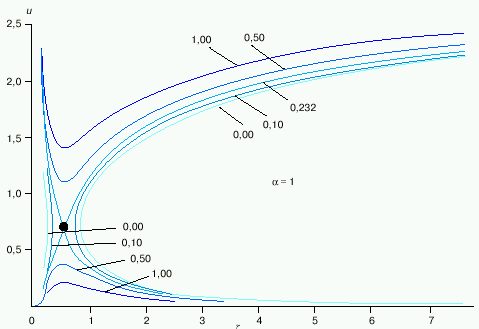
Radial'nye profili skorosti solnechnogo vetra v sluchae izotermicheskoi ($\alpha$ = 1) korony pri razlichnoi temperature poslednei predstavleny na ris. 2. Iz privedennyh krivyh vidno, chto reshenie dostatochno chuvstvitel'no k granichnym usloviyam. Tak, naprimer, pri T0 = 0,5 106 K skorost' solnechnogo vetra na orbite Zemli okazyvaetsya ravnoi 260 km/s, a pri T = 4 106 K - okolo 1150 km/s, chto v celom ne protivorechit eksperimental'nym dannym (sm. tabl. 1 iz [4]). V to zhe vremya rasschitannaya plotnost' plazmy na orbite Zemli 25-40 sm- 3 vmesto real'nyh 5-10 sm- 3.

Ris. 2.Radial'nye profili skorosti solnechnogo vetra v modeli Parkera pri razlichnyh temperaturah T korony.

Kak vidno iz tablicy, skorost' solnechnogo vetra menyaetsya v dostatochno shirokom diapazone - ot ~ 300 do ~ 700 km/s. Kazalos' by, eti variacii legko ob'yasnimy v ramkah modeli Parkera sootvetstvuyushimi variaciyami temperatury korony (sm. ris. 2). Odnako neposredstvennye nablyudeniya svidetel'stvuyut, chto istochnikom rekurrentnyh vysokoskorostnyh potokov yavlyayutsya koronal'nye dyry (sm. nizhe), v kotoryh temperatura korony sushestvenno nizhe srednei. V svyazi s etim obratim vnimanie na to, chto, soglasno modeli, skorost' solnechnogo vetra pomimo temperatury korony zavisit takzhe ot velichiny pokazatelya politropy $\alpha$: chem bol'she $\alpha$, tem men'she skorost' solnechnogo vetra na orbite Zemli. Nailuchshee sootvetstvie mezhdu model'nymi raschetami i eksperimental'nymi dannymi polucheno Parkerom pri $\alpha$ = 1,1 vblizi Solnca i $\alpha$ = 5/3 na bol'shih rasstoyaniyah ot nego.

Odnako v svyazi s maloi velichinoi pokazatelya $\alpha$ voznikaet zatrudnenie sleduyushego roda: pri $\alpha\rightarrow 1$ gradient temperatury $\partial T / \partial r \rightarrow 0$. Pri etom potok tepla, obuslovlennyi teploprovodnost'yu, takzhe stremitsya k nulyu. Takim obrazom, dlya podderzhaniya dostatochno vysokoi temperatury solnechnogo vetra trebuyutsya dopolnitel'nye neteplovye istochniki energii, svyazannye, skoree vsego, s dissipaciei energii al'fvenovskih voln [3].

Vklad MGD-voln v teplovuyu energiyu i impul's solnechnogo vetra obsuzhdayutsya v ryade publikacii. Obzor etih issledovanii i ih dal'neishee razvitie dany I. Chasheem i V. Shishovym (1987 god). Vybrav sootvetstvuyushim obrazom intensivnost' i spektr MGD-voln v osnovanii korony, mozhno poluchit' ne tol'ko sootvetstvuyushuyu eksperimental'nym dannym skorost' solnechnogo vetra na orbite Zemli, no i neobhodimuyu plotnost' plazmy.

Vmeste s tem model', razvivaemaya v ramkah odnozhidkostnoi gidrodinamiki, ne v sostoyanii ob'yasnit' nablyudaemuyu raznost' elektronnoi i ionnoi temperatur v solnechnom vetre (sm. tabl. 1).

Tablica 1. Parametry solnechnogo vetra na orbite Zemli
Parametr, razmernost' Srednyaya velichina Solnechnyi veter
    medlennyi vysoko skorostnoi
n, sm-3 8,7 11,9 3,9
$\upsilon$, km/s 468 327 702
n$\upsilon$, sm-2 s-1 3,8 $\cdot$ 108 3,9 $\cdot$ 108 2,7 $\cdot$ 108
Tp , K 7 $\cdot$ 104 3,4 $\cdot$ 104 2,3 $\cdot$ 105
Te , K 1,4 $\cdot$ 105 1,3 $\cdot$ 105 1,0 $\cdot$ 105
Te / Tp 1,9 4,4 0,45

Sleduet zametit', chto odnozhidkostnye modeli gidrodinamiki primenimy v fizike plazmy lish' v tom sluchae, kogda chastota stolknovenii elektronov s ionami dostatochno velika, chto obespechivaet effektivnyi obmen impul'som mezhdu elektronnoi i ionnoi komponentami plazmy i sootvetstvenno ravenstvo ih temperatur. P.A. Sturrock i R.E. Hartle (1966 god) obratili vnimanie na to, chto v solnechnom vetre vsledstvie bystrogo ubyvaniya plotnosti plazmy s rasstoyaniem ot Solnca poslednee uslovie mozhet ne vypolnyat'sya i temperatura ionov mozhet sushestvenno otlichat'sya ot temperatury elektronov. Pri etom, poskol'ku ionnaya teploprovodnost' otnositel'no mala, protonnaya komponenta korony Solnca rasshiryaetsya pochti adiabaticheski i sootvetstvenno bystro ohlazhdaetsya. V to zhe vremya teploprovodnost' elektronnoi komponenty plazmy otnositel'no velika, v svyazi s chem temperatura poslednei padaet s rasstoyaniem dostatochno medlenno, chto v celom ne protivorechit eksperimental'nym dannym (sm. tabl. 1).

Takoe otnositel'no nezavisimoe sushestvovanie elektronnoi i ionnoi komponent plazmy opisyvaetsya v ramkah dvuhzhidkostnoi gidrodinamiki. Pri etom v uravnenii dvizheniya (3) gazovoe davlenie sleduet zamenit' summoi davlenii elektronnogo i ionnogo gazov P = Pe + Pi = nk(Te + Ti ). Krome togo, v sluchae dvuhzhidkostnoi gidrodinamiki uravnenie gazovogo sostoyaniya obychno zamenyayut uravneniem sohraneniya energii, zapisannym otdel'no dlya elektronnoi i ionnoi komponent, tak chto sistema uravnenii (2) - (4) prinimaet vid [1]

$$nm_{i}\upsilon \frac{d \upsilon}{dr}=-\frac{d}{dr} (nk(T_{e}+T_{i}))-nm_{i}\frac {GM_{\odot}}{r^2}\,;$$ (15)
$$n\upsilon A = n_{0}\upsilon_{0} A_{0}\,;$$ (16)
$$\frac{1}{r^2}\frac{d}{dr}\left[nm_{i}\upsilon r^{2}\left( \frac{1}{2}\upsilon^{2}+\frac{3}{2}\frac {P_{i}}{nm_{i}} \right) \right]=-\frac{1}{r^{2}}\frac{d}{dr}(P_{i}\upsilon r^{2})-$$ (17)
$$-nm_{i}\upsilon \frac{GM_{\odot}}{r^{2}}+\frac{1}{r^{2}}\frac{d}{dr}\left( r^{2}k_{i} \frac{dT_{i}}{dr} \right) + \frac{3}{2}\nu nK(T_{e}-T_{i})\,;$$
$$\frac{1}{r^2} \frac{d}{dr} \left[ nm_{e} \upsilon r^{2} \left( \frac{1}{2} \upsilon^{2}+ \frac{3}{2}\frac {P_{e}}{nm_{e}} \right) \right]=-\frac{1}{r^{2}}\frac{d}{dr}(P_{e} \upsilon r^{2})-$$ (18)
$$-nm_{e}\upsilon \frac{GM_{\odot}}{r^{2}}+\frac{1}{r^{2}} \frac{d}{dr} \left( r^{2}k_{e}\frac{dT_{e}}{dr} \right) + \frac{3}{2}\nu nK(T_{i}-T_{e})\,;$$

zdes' $m_i$ i $m_e$ - massa iona i elektrona sootvetstvenno, $T_i$ i $T_e$ - ionnaya i elektronnaya temperatura; $k_{i, e}$ - koefficient ionnoi (elektronnoi) teploprovodnosti, $K$ - postoyannaya Bol'cmana i $\nu$ - chastota stolknovenii ionov s elektronami.

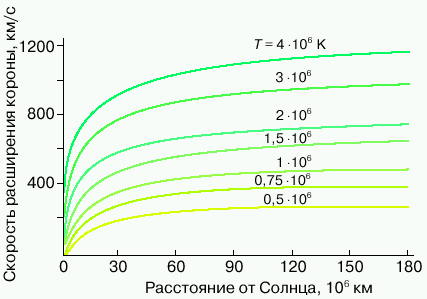
Rezul'taty chislennogo integrirovaniya sistemy uravnenii (15)- (18) predstavleny na ris. 3 iz [1] . Krivaya 1 sootvetstvuet odnozhidkostnoi modeli, krivye 2 i 3 pokazyvayut izmenenie s rasstoyaniem elektronnoi i ionnoi temperatury solnechnogo vetra v dvuhzhidkostnoi modeli. Kak vidno iz risunka, na orbite Zemli (r = 215$R_{\odot}$ Tp = 4,4 103 K i Te = 3,4 105 K.

Ris. 3. Izmenenie s rasstoyaniem ot Solnca $r_{\odot}$ temperatury T solnechnogo vetra v odnozhidkostnoi modeli (1 ), elektronnoi (2 ) i ionnoi (3 ) temperatur v dvuhzhidkostnoi modeli.

Takim obrazom, predskazyvaemaya model'yu temperatura elektronov okazyvaetsya vdvoe bol'she, a temperatura protonov - na poryadok men'she real'noi temperatury chastic v solnechnom vetre (sm. tabl. 1). Takoe nesootvetstvie teoreticheskih i eksperimental'nyh dannyh mozhno ustranit', predpolozhiv sushestvovanie dopolnitel'nyh istochnikov nagreva plazmy, prichem preimushestvenno ee ionnoi komponenty. Etomu trebovaniyu udovletvoryayut upomyanutye vyshe al'fvenovskie volny. Delo v tom, chto, hotya sami al'fvenovskie volny v solnechnom vetre pochti ne pogloshayutsya, oni effektivno transformiruyutsya v hode chetyrehvolnovogo vzaimodeistviya v magnitozvukovye volny. Poslednie zhe v usloviyah, harakternyh dlya solnechnogo vetra, dissipiruyut v rezul'tate rezonansnogo vzaimodeistviya s protonami, kotorye pri etom zametno nagrevayutsya.

Parametry solnechnogo vetra na orbite Zemli, poluchennye A. Barnes i dr. v 1971 godu v ramkah dvuhzhidkostnoi modeli s uchetom dopolnitel'nogo istochnika energii v vide MGD-voln, predstavleny v tabl. 2.

Tablica 2. Parametry solnechnogo vetra na orbite Zemli v dvuhzhidkostnoi modeli Barnesa
Plotnost' plazmy n, sm-3 15
Skorost' $\upsilon$, km/s 330
Potok kineticheskoi energii, erg $\cdot$ sm-2 $\cdot$ s 0,46
Protonnaya temperatura Tp , K 3,2 $\cdot$ 104
Elektronnaya temperatura Te , K 2,2 $\cdot$ 105
Otnoshenie Te / Tp 6,9

Rasschitannye parametry solnechnogo vetra na orbite Zemli okazyvayutsya blizkimi k nablyudaemym parametram medlennogo solnechnogo vetra (sm. tabl. 1). V to zhe vremya parametry vysokoskorostnyh potokov v solnechnom vetre zametno otlichayutsya ot predskazyvaemyh model'yu. V chastnosti, temperatura protonov v etih potokah okazyvaetsya vyshe temperatury elektronov, chto, po-vidimomu, svidetel'stvuet o povyshennoi intensivnosti al'fvenovskih voln v oblasti ih istochnika na Solnce.

Rassmotrim podrobnee vysokoskorostnoi solnechnyi veter i obsudim ego vozmozhnye istochniki.

Vysokoskorostnoi solnechnyi veter

Kak vidno iz dannyh, predstavlennyh v tabl. 1, vysokoskorostnoi solnechnyi veter harakterizuetsya povyshennoi skorost'yu (okolo 700 km/s), ponizhennoi plotnost'yu plazmy (n = 4 sm-3) i povyshennoi ionnoi temperaturoi. Odnako, prezhde chem obsuzhdat' vozmozhnye istochniki etih potokov, napomnim, chto sushestvuyut po men'shei mere dva roda takih potokov: rekurrentnye i sporadicheskie.

Rekurrentnye potoki vysokoskorostnogo solnechnogo vetra otlichayutsya prezhde vsego tem, chto sushestvuyut v techenie mnogih mesyacev, regulyarno poyavlyayas' v okrestnostyah Zemli primerno cherez 27 dnei (period oborota Solnca), chto svidetel'stvuet ob otnositel'no bol'shom vremeni zhizni ih istochnikov. V techenie mnogih let proishozhdenie etih potokov ostavalos' zagadkoi, poskol'ku im ne sootvetstvovali kakie-libo vidimye osobennosti na poverhnosti Solnca. Odnako v nastoyashee vremya mozhno schitat' dokazannym, chto obsuzhdaemye potoki zarozhdayutsya na Solnce v oblasti tak nazyvaemyh koronal'nyh dyr.

Koronal'nye dyry otchetlivo vidny na poluchaemyh na kosmicheskih apparatah fotografiyah Solnca v rentgenovskom i krainem ul'trafioletovom diapazonah spektra solnechnogo izlucheniya (sm. ris. 4), gde oni fiksiruyutsya kak obshirnye oblasti ponizhennoi (v neskol'ko raz) intensivnosti izlucheniya, prostirayushiesya ot polyarnyh shirot do ekvatora ili dazhe v protivopolozhnoe polusharie.

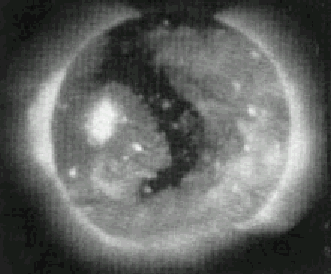Ris. 4. Fotografiya Solnca v rentgenovskom izluchenii 21 avgusta 1973 goda.

Protyazhennost' koronal'nyh dyr po dolgote sostavlyaet 30° - 90°. Sootvetstvenno vremya prohozhdeniya koronal'noi dyry cherez central'nyi meridian Solnca (vsledstvie vrasheniya poslednego) sostavlyaet 3-6 sutok, chto vpolne soglasuetsya s dlitel'nost'yu sushestvovaniya sootvetstvuyushih vysokoskorostnyh potokov v okrestnostyah Zemli [1]. Ponizhennaya intensivnost' rentgenovskogo izlucheniya v oblasti koronal'nyh dyr mozhet opredelyat'sya kak ponizhennoi plotnost'yu plazmy v etih oblastyah, tak i ee ponizhennoi temperaturoi. Deistvitel'no, nazemnye nablyudeniya korony vo vremya solnechnyh zatmenii pokazyvayut, chto v korone sushestvuyut, v osobennosti v vysokih shirotah, oblasti s otnositel'no nizkoi plotnost'yu plazmy. V to zhe vremya i temperatura plazmy v oblasti koronal'nyh dyr okazyvaetsya sushestvenno ponizhennoi. Tak, naprimer, pri nablyudeniyah izlucheniya Solnca v radiodiapazone yarkostnaya temperatura v oblasti koronal'nyh dyr sostavlyaet okolo 0,8 106 K, chto sushestvenno nizhe temperatury spokoinoi korony, i plotnost' plazmy v koronal'noi dyre sostavlyaet 0,25 plotnosti spokoinoi korony.

Takim obrazom, koronal'nye dyry deistvitel'no predstavlyayut soboi oblasti ponizhennoi plotnosti plazmy i ee otnositel'no nizkoi temperatury. Chem vyzyvayutsya ukazannye osobennosti korony v etih oblastyah, ne sovsem yasno. V svyazi s etim obrashaet na sebya vnimanie to, chto koronal'nye dyry, kak pravilo, sovpadayut s oblastyami unipolyarnogo magnitnogo polya s kvaziradial'nymi ili slegka rashodyashimisya silovymi liniyami [4]. Otkrytye silovye linii magnitnogo polya ne prepyatstvuyut radial'nomu rasshireniyu koronal'noi plazmy, chto mozhet ob'yasnit' ponizhennuyu plotnost' poslednei v oblasti dyr i uvelichenie skorosti generiruemogo v nih solnechnogo vetra. Vmeste s tem uvelichenie skorosti vetra, obuslovlennoe blagopriyatnoi konfiguraciei silovyh linii magnitnogo polya, ne mozhet kompensirovat' ee umen'sheniya, svyazannogo s nizkoi temperaturoi plazmy v rassmatrivaemyh oblastyah, i dlya ob'yasneniya poyavleniya vysokoskorostnyh potokov opyat' prihoditsya predpolozhit' nalichie v koronal'nyh dyrah moshnogo istochnika MGD-voln. K sozhaleniyu, pryamyh podtverzhdenii sushestvovaniya takih voln v oblasti koronal'nyh dyr poka ne polucheno.

Sporadicheskie vysokoskorostnye potoki. Vtoroi tip vysokoskorostnyh potokov v solnechnom vetre - eto kratkovremennye (vremya probega mimo Zemli $\tau$ = 1-2 sutok), chasto chrezvychaino intensivnye (skorost' solnechnogo vetra do 1200 km/s) potoki, imeyushie ves'ma bol'shuyu dolgotnuyu protyazhennost'. Dvigayas' v mezhplanetnom prostranstve, zapolnennom plazmoi otnositel'no medlennogo spokoinogo solnechnogo vetra, vysokoskorostnoi potok kak by sgrebaet etu plazmu, v rezul'tate chego pered ego frontom obrazuetsya dvizhushayasya vmeste s nim otoshedshaya udarnaya volna. Prostranstvo mezhdu frontom potoka i frontom otoshedshei udarnoi volny zapolneno otnositel'no plotnoi (neskol'ko desyatkov chastic v 1 sm3) i goryachei plazmoi.

Ranee predpolagalos', chto sporadicheskie potoki v solnechnom vetre obuslovleny solnechnymi vspyshkami [1] i im podobnymi yavleniyami. Odnako v poslednee vremya obshestvennoe mnenie na etot schet izmenilos', i bol'shinstvo issledovatelei, v osobennosti zarubezhnyh, priderzhivayutsya tochki zreniya, soglasno kotoroi sporadicheskie vysokoskorostnye potoki v solnechnom vetre obuslovleny tak nazyvaemymi koronal'nymi vybrosami.

Koronal'nye vybrosy, naibolee otchetlivo nablyudaemye vblizi limba Solnca, predstavlyayut soboi nekotorye otnositel'no protyazhennye plazmennye obrazovaniya, dvizhushiesya v korone Solnca vverh ot ee osnovaniya. Vyvod o tom, chto sporadicheskie potoki v solnechnom vetre svyazany imenno s koronal'nymi vybrosami (ili CME), a ne so vspyshkami, osnovan na sleduyushih eksperimental'nyh faktah: 1) nesmotrya na statisticheski znachimuyu svyaz' mezhdu sporadicheskimi potokami i solnechnymi vspyshkami, odnoznachnaya svyaz' mezhdu nimi otsutstvuet, to est', s odnoi storony, nablyudayutsya vspyshki, ne vyzyvayushie mezhplanetnyh udarnyh voln, i, s drugoi - nablyudayutsya vysokoskorostnye potoki, ne predvaryaemye vspyshkami, i 2) solnechnye vspyshki neposredstvenno ne svyazany s koronal'nymi vybrosami. Svyaz' mezhdu mezhplanetnymi udarnymi volnami, koronal'nymi vybrosami i solnechnymi vspyshkami detal'no issledovalas' N. Sheeley i dr. (1985 god), kotorye, v chastnosti, pokazali, chto 72% udarnyh voln, nablyudavshihsya na bortu kosmicheskogo apparata "Helios-1", byli svyazany s bol'shimi nizkoshirotnymi koronal'nymi vybrosami. V to zhe vremya lish' 52% teh zhe udarnyh voln byli svyazany s solnechnymi vspyshkami.

V rezul'tate podrobnogo analiza etih dannyh udalos' pokazat' [5],[6], chto esli isklyuchit' iz spiska udarnye volny, nablyudaemye za limbom Solnca, to chislo voln, svyazannyh so vspyshkami, vozrastaet do 85%, to est' svyaz' udarnyh voln so vspyshkami okazyvaetsya nichut' ne huzhe, chem s koronal'nymi vybrosami. Krome togo, kak pokazali Harrison i dr. (1990 god), koronal'nye vybrosy i vspyshki svyazany s odnimi i temi zhe aktivnymi oblastyami na Solnce, i bystrye vybrosy (so skorost'yu poryadka 1000 km/s), s kotorymi obychno svyazana mezhplanetnaya udarnaya volna, nachinayut svoe dvizhenie v korone odnovremenno s nachalom vspyshki.

Takim obrazom, vyvod o neprichastnosti solnechnyh vspyshek k mezhplanetnym udarnym volnam predstavlyaetsya ne vpolne ubeditel'nym, i my po-prezhnemu budem schitat' solnechnye vspyshki odnim iz osnovnyh istochnikov vysokoskorostnyh sporadicheskih potokov v solnechnom vetre.

Chto kasaetsya mehanizma generacii samih vspyshek (i, estestvenno, svyazannyh s nimi potokov), to naibolee populyarnoi v nastoyashee vremya yavlyaetsya predlozhennaya v 1964 godu Petchekom model' vspyshki, osnovannaya na gipoteze o magnitnom peresoedinenii (sm. [7]). Razvitie solnechnoi vspyshki v ramkah modeli Petcheka predstavleno na ris. 5.

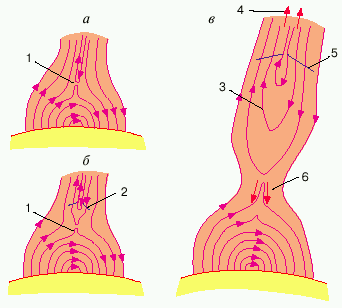Ris. 5. Razvitie vspyshki v modeli Starroka: 1 - liniya peresoedineniya, 2 - formiruyushayasya udarnaya volna, 3 - ezhektiruemaya plazma, 4 - vysokoenergichnye chasticy, 5 - udarnaya volna, 6 - bystrye elektrony.

V etoi modeli silovye linii magnitnogo polya aktivnoi oblasti okazyvayutsya, nachinaya s nekotorogo urovnya, razorvannymi i obrazuyut dve silovye trubki s antiparallel'nymi polyami, razdelennymi tokovym sloem. V nekotoryi moment iz-za razvitiya ionno-zvukovoi ili ionno-ciklotronnoi neustoichivosti provodimost' plazmy v nekotoroi tochke 1 (ris. 5a) v plazmennom sloe rezko padaet, v rezul'tate chego tokovyi sloi razryvaetsya i silovye linii magnitnogo polya peresoedinyayutsya. Magnitnaya energiya bystro perehodit v kineticheskuyu i teplovuyu energiyu plazmy i proishodyat intensivnyi razogrev i uskorenie plazmy (ris. 5b). Uskorennye chasticy, dvigayas' vdol' otkrytyh silovyh linii magnitnogo polya, pokidayut hromosferu i vybrasyvayutsya v mezhplanetnoe prostranstvo (ris. 5v). Pri etom dvizhushiesya vverh energichnye elektrony, prohodya cherez koronu i vzaimodeistvuya s nei, mogut vyzyvat' vspleski radioizlucheniya. Chastota radioizlucheniya vsledstvie umen'sheniya koncentracii fonovoi plazmy bystro umen'shaetsya po mere dvizheniya elektronov vverh (chto sootvetstvuet tak nazyvaemym vspleskam radioizlucheniya III tipa).

Chasticy, dvizhushiesya vdol' silovyh linii magnitnogo polya k Solncu, nagrevayut plazmu v nizhnei hromosfere i fotosfere, vyzyvaya uvelichenie yarkosti vodorodnyh emissii i obrazovanie vysokotemperaturnogo koronal'nogo oblaka. Plazma, uskoryaemaya v napravlenii ot Solnca, formiruet vysokoskorostnoi potok i svyazannuyu s nim udarnuyu volnu.

Zaklyuchenie

Superpoziciya opisannyh vyshe potokov solnechnoi plazmy i ih vzaimodeistvie i sozdayut tu slozhnuyu i nepreryvno izmenyayushuyusya sistemu, kotoraya nazyvaetsya solnechnym vetrom.

V kratkom obzore sovremennyh predstavlenii o morfologii i mehanizmah generacii solnechnogo vetra my smogli obsudit' lish' samye obshie i naibolee polno issledovannye harakteristiki etih processov, chto mozhet sozdat' neskol'ko lozhnoe predstavlenie o deistvitel'nom sostoyanii problemy. V svyazi s etim sleduet eshe raz podcherknut', chto nami opusheny mnogie, v tom chisle i ves'ma sushestvennye, detali rassmatrivaemyh processov (naprimer, mehanizm formirovaniya mezhplanetnogo magnitnogo polya), bez otchetlivogo ponimaniya kotoryh predstavlennaya vyshe model' solnechnogo vetra ostaetsya ne bolee chem gipotezoi, hotya i ves'ma veroyatnoi.

Bolee podrobnoe izlozhenie obsuzhdaemyh voprosov predstavleno v upomyanutyh vyshe knigah [1]-[4] i obzorah [6], [7].

Literatura

[1] Hundhauzen A. Rasshirenie korony i solnechnyi veter. M.: Mir, 1976. 302 s.
[2] Gibson E. Spokoinoe Solnce. M.: Mir, 1977. 408 s.
[3] Parker E.N. Dinamicheskie processy v mezhplanetnoi srede. M.: Mir, 1965. 362 s.
[4] Kovalenko V.A. Solnechnyi veter. M.: Nauka, 1983. 272 s.
[5] Pudovkin M.I. // J. Geophys. Res. 1995. V. 100. No A5. P. 7917.
[6] Pudovkin M.I. // Rept. Progr. in Phys. 1995. V. 58. No 9. P. 929.
[7] Pudovkin M.I., Semenov V.S. Teoriya peresoedineniya i vzaimodeistvie solnechnogo vetra s magnitosferoi Zemli. M.: Nauka, 1985. 126 s.

Publikacii s klyuchevymi slovami: mehanizm vozniknoveniya solnechnogo vetra - teoriya Parkera - magnitogidrodinamicheskie volny - Solnechnyi veter
Publikacii so slovami: mehanizm vozniknoveniya solnechnogo vetra - teoriya Parkera - magnitogidrodinamicheskie volny - Solnechnyi veter
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 2.0 [golosov: 28]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya