Astronet > Obratnye zadachi v astrofizike

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Obratnye zadachi v astrofizike

A.M.ChEREPAShUK

Gosudarstvennyi astronomicheskii institut im. P.K. Shternberga Moskovskogo gosudarstvennogo universiteta im. M.V. Lomonosova

Bol'shinstvo zadach interpretacii astronomicheskih nablyudatel'nyh dannyh yavlyayutsya obratnymi i nekorrektno postavlennymi. Sovremennye nauchno obosnovannye metody, osnovannye na predlozhennoi A.N.Tihonovym idee regulyariziruyushego algoritma, pozvolyayut poluchat' ustoichivye priblizhennye resheniya nekorrektnyh zadach. Primenenie etih metodov k obratnym zadacham astrofiziki pozvolyaet delat' vazhnye vyvody o prirode astronomicheskih ob'ektov.

Vvedenie

Astrofizika yavlyaetsya nablyudatel'noi naukoi, poskol'ku issledovatel' v podavlyayushem bol'shinstve sluchaev ne imeet vozmozhnosti pryamogo vozdeistviya na izuchaemyi ob'ekt. Vyvody o prirode issleduemyh ob'ektov astrofiziki delayut na osnove analiza kosvennoi informacii, kotoraya zaklyuchena v postupayushih iz Kosmosa razlichnyh izlucheniyah: elektromagnitnom (ot gamma-kvantov do radiovoln), neitrinnom, korpuskulyarnom (kosmicheskie luchi), gravitacionno-volnovom (registraciya kotorogo namechaetsya v blizhaishei perspektive). Harakteristiki etih izluchenii (intensivnost', spektr, polyarizaciya, peremennost' i t.p.) yavlyayutsya sledstviyami teh processov, o prirode kotoryh dolzhen sudit' astrofizik. Lish' v redkih sluchayah astrofiziki mogut neposredstvenno vozdeistvovat' na izuchaemyi ob'ekt: eto issledovanie meteoritnogo veshestva, kotoroe vypadaet na Zemlyu iz mezhplanetnogo prostranstva (upomyanem v etoi svyazi nedavnee otkrytie amerikanskimi uchenymi sledov zhiznedeyatel'nosti mikroorganizmov v marsianskom meteorite), a takzhe izuchenie poverhnostei planet s pomosh'yu aktivnyh kosmicheskih apparatov, spuskaemyh na ih poverhnost'. V podavlyayushem zhe bol'shinstve sluchaev astrofiziki vynuzhdeny po sledstviyam nekotoryh processov, protekayushih na nebesnyh telah, sudit' o prichinah, ih porodivshih, to est' reshat' obratnye zadachi.

Reshenie pryamoi zadachi svyazano s otyskaniem sledstviya nekotorogo processa po ego izvestnoi prichine. Naprimer, mozhno na lyuboi moment vremeni rasschitat' polozheniya planet Solnechnoi sistemy, znaya glavnuyu prichinu, kotoraya lezhit v osnove ih dvizheniya, - zakon vsemirnogo tyagoteniya N'yutona s popravkami za effekty obshei teorii otnositel'nosti (kotorye sil'nee vsego skazyvayutsya na progressivnom smeshenii perigeliya Merkuriya 43 uglovyh sekundy v stoletie). Odnako, kogda N'yuton reshal obratnuyu zadachu - vyvodil svoi znamenityi zakon vsemirnogo tyagoteniya iz nablyudaemogo dvizheniya planet, obobshennogo v izvestnyh zakonah Keplera, on stolknulsya so znachitel'no bolee slozhnoi problemoi. I tol'ko ogromnyi nablyudatel'nyi material po mnogim planetam v sochetanii s genial'nost'yu i tonkoi fizicheskoi intuiciei pozvolil N'yutonu uspeshno reshit' etu tipichnuyu obratnuyu zadachu.

V otlichie ot pryamyh zadach trudnosti resheniya obratnyh zadach svyazany s tem, chto odin i tot zhe effekt mozhet byt' porozhden raznymi prichinami. Naprimer, izvestno, chto esli nagret' vodu pri atmosfernom davlenii do temperatury 100°C, to ona zakipit. Odnako iz togo fakta, chto voda kipit, vovse ne sleduet, chto ona nagreta do temperatury 100°C, poskol'ku voda mozhet kipet' i pri komnatnoi temperature, no pri dostatochno nizkom atmosfernom davlenii. Horosho izvestno, chto v gorah nevozmozhno svarit' risovuyu kashu, poskol'ku voda tam kipit pri temperature okolo 80°C. Takim obrazom, effekt kipeniya vody mozhet byt' vyzvan raznymi prichinami: libo vysokoi temperaturoi, libo nizkim davleniem.

Privedennyi primer naglyadno illyustriruet, kakoi tonkoi i delikatnoi proceduroi yavlyaetsya reshenie obratnoi zadachi interpretacii nablyudatel'nyh dannyh. Esli dlya resheniya pryamoi zadachi dostatochno znat' odnu prichinno-sledstvennuyu svyaz', to dlya uspeshnogo resheniya obratnoi zadachi etogo yavno nedostatochno i neobhodimo uchityvat' mnogie prichinno-sledstvennye svyazi, soprovozhdayushie izuchaemyi process, i, sledovatel'no, imet' gorazdo bolee bogatyi opyt i eksperimental'nyi material, chem dlya resheniya pryamoi zadachi.

V matematike horosho izvestno, chto podavlyayushee bol'shinstvo obratnyh zadach yavlyayutsya nekorrektno postavlennymi - malym vozmusheniyam ishodnyh dannyh (dannyh nablyudenii) mogut sootvetstvovat' skol' ugodno bol'shie vozmusheniya resheniya. Kak otmecheno francuzskim uchenym Zh. Adamarom v 1939 godu, zadacha nazyvaetsya korrektno postavlennoi (korrektnoi), esli:

ee reshenie sushestvuet,
reshenie edinstvenno i
reshenie nepreryvno zavisit ot vhodnyh dannyh, to est' ustoichivo po otnosheniyu k malym vozmusheniyam (oshibkam) dannyh nablyudenii.

Esli hotya by odno iz etih treh uslovii ne vypolnyaetsya, zadacha nazyvaetsya nekorrektno postavlennoi.

Naibolee chasto v sluchae obratnyh zadach narushaetsya uslovie 3, to est' uslovie ustoichivosti resheniya. V etom sluchae voznikaet paradoksal'naya situaciya: nesmotrya na to chto zadacha matematicheski sformirovana, ee reshenie nevozmozhno poluchit' obychnymi metodami. Deistvitel'no, kakoi smysl imeet reshenie, kotoroe ispytyvaet formal'no beskonechno bol'shie vozmusheniya pri malyh vozmusheniyah rezul'tatov nablyudenii, kotorye vsegda poluchayutsya s nekotoroi neopredelennost'yu (oshibkoi). Imenno poetomu Adamar i prishel k zaklyucheniyu, chto nekorrektnye zadachi ne imeyut prakticheskogo smysla. No tragediya zaklyuchaetsya v tom, chto po sushestvu vse zadachi obrabotki i interpretacii dannyh astronomicheskih nablyudenii, kak, vprochem, i rezul'tatov mnogih fizicheskih eksperimentov, yavlyayutsya obratnymi i, sledovatel'no, nekorrektno postavlennymi. Do poyavleniya sovremennyh nauchno obosnovannyh metodov issledovatel' libo, ispol'zuya detal'nuyu fizicheskuyu model' izuchaemogo yavleniya, svodil obratnuyu zadachu k nahozhdeniyu nebol'shogo chisla parametrov, libo, osnovyvayas' na fizicheskoi intuicii, otbiral iz mnozhestva dopustimyh reshenii to, kotoroe luchshe vsego sootvetstvuet zdravomu smyslu. Odnako takie rezul'taty resheniya obratnoi zadachi vsegda ostavlyayut chuvstvo neudovletvorennosti: v pervom sluchae chasto byvaet, chto detal'naya fizicheskaya model', dopuskayushaya zhestkuyu parametrizaciyu resheniya, neadekvatna ispol'zuemym nablyudatel'nym dannym (chto privodit k bol'shim ostatochnym ukloneniyam nablyudatel'nyh dannyh ot teoreticheskih predskazanii), vo vtorom sluchae vybor resheniya sub'ektiven, chto neharakterno dlya nauchnogo metoda issledovanii.

Matematicheski pod obratnoi zadachei ponimaetsya zadacha otyskaniya funkcii z(s) po funkcii u(x), poluchaemoi iz eksperimenta ili nablyudenii, iz uravneniya vida

$u(x) = A[x, z(s)]$

(1)

gde A est' nekotoryi operator, ustanavlivayushii prichinno-sledstvennuyu svyaz' mezhdu z(s) i u(x). V uravnenii (1) po nablyudaemym sledstviyam u(x) processa my dolzhny sudit' o prichinah z(s), porodivshih ego.

Vo mnogih sluchayah obratnaya zadacha (1) mozhet byt' predstavlena integral'nym uravneniem Fredgol'dma 1-go roda

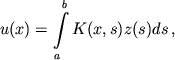
$u(x)=\int\limits_a^b K(x,s)z(s)ds\,,$

(2)

gde K(x, s) - yadro (nepreryvnoe ili kvadratichno summiruemoe po peremennym x, s), kotoroe opisyvaet konkretnuyu model' issleduemogo processa.

Matematicheskie trudnosti resheniya obratnyh zadach svyazany s tem, chto obratnyi operator A^-1 (sm. uravnenie (1)) ne yavlyaetsya nepreryvnym. Poetomu esli dannye nablyudenii u(x) polucheny s nekotoroi oshibkoi $\delta$ (oboznachim priblizhennye dannye simvolom $u_{\delta}(x)$ ), to sootvetstvuyushee priblizhennoe reshenie, poluchennoe standartnym metodom,

$z_{\delta}(s) = A^{-1}[u_{\delta}(x)]$

(3)

budet skol' ugodno sil'no otklonyat'sya ot resheniya, sootvetstvuyushego ideal'no tochnym vhodnym dannym u(x).

Predlagaemye ranee metody resheniya obratnyh nekorrektnyh zadach osnovyvalis' prezhde vsego na intuicii avtorov, i hotya v ryade obratnyh zadach udavalos' poluchit' vazhnuyu fizicheskuyu informaciyu, neobhodimost' v strogoi matematicheskoi postanovke i razrabotke chislennyh metodov resheniya etogo vazhneishego dlya sovremennogo estestvoznaniya kruga problem ostro nazrela k 60-m godam, osobenno v svyazi s shirokim vnedreniem komp'yuterov v praktiku nauchnyh issledovanii.

Metody resheniya nekorrektnyh zadach poluchili intensivnoe razvitie v 60-e gody. Opredelyayushuyu rol' zdes' sygrali raboty A.N. Tihonova, M.M. Lavrent'eva, V.K. Ivanova i drugih matematikov. Seichas mozhno govorit' o nauchnoi shkole A.N. Tihonova, kotoraya sozdala matematicheskuyu teoriyu nekorrektno postavlennyh zadach, razrabotala effektivnye metody ih resheniya (regulyariziruyushie algoritmy).

Sut' dela sostoit v tom, chto nekorrektno postavlennye zadachi rassmatrivayutsya kak fizicheski nedoopredelennye. Oni ploho postavleny, mnozhestva ih priblizhennyh reshenii ochen' shiroki, dazhe neogranichenny. Poetomu nekorrektnye zadachi nuzhno doopredelit'. Dlya etogo neobhodima dopolnitel'naya informaciya ob iskomom reshenii z(s), vytekayushaya iz obshirnogo opyta vsestoronnih issledovanii dannogo processa. Vazhno podcherknut', chto eta dopolnitel'naya informaciya ob iskomom reshenii dolzhna byt' izvestna a priori, do resheniya sootvetstvuyushei nekorrektnoi zadachi. Apriornaya informaciya pozvolyaet sformulirovat' kriterii otbora priblizhennogo resheniya iz mnozhestva priblizhennyh reshenii uravneniya (1) i postroit' regulyariziruyushii algoritm.

Takoi informaciei mogut sluzhit' apriornye svedeniya o gladkosti iskomogo resheniya z(s), ego monotonnosti, vypuklosti, neotricatel'nosti, prinadlezhnosti k konechno-parametricheskomu semeistvu i t. p.

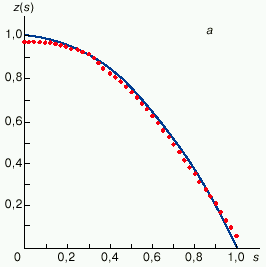
Na ris. 1a, privedeno tochnoe i priblizhennoe reshenie nekorrektnoi zadachi - integral'nogo uravneniya Fredgol'ma 1-go roda (2) prichem priblizhennoe reshenie polucheno s pomosh'yu regulyariziruyushego algoritma - suzheniya mnozhestva dopustimyh reshenii do mnozhestva vypuklyh funkcii. Popytka resheniya etoi zhe zadachi bez regulyarizacii yavlyaetsya bezuspeshnoi (ris. 1b).

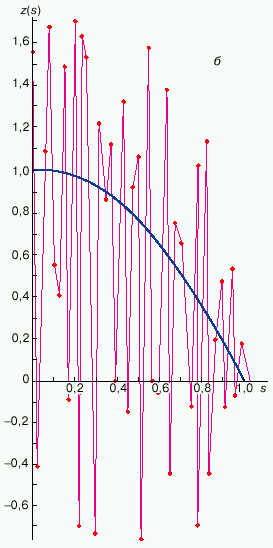Ris. 1. Rezul'taty resheniya obratnoi zadachi, opisyvaemoi integral'nym uravneniem (2) s yadrom K(x,s)=1/(1+100(x-s)²). Sploshnoi liniei predstavleno tochnoe reshenie z(s), kotoroe bylo zadano zaranee. Eto reshenie podstavlyalos' pod znak integrala v uravnenie (2) i vychislyalas' sootvetstvuyushaya emu funkciya u(x) - ideal'no tochnye "vhodnye dannye" obratnoi zadachi (2). Zatem v poluchennuyu funkciyu u(x) vnosilas' pogreshnost' $\delta$ = 3% ot maksimal'nogo znacheniya i reshalas' obratnaya zadacha: po vozmushennoi funkcii $u_{\delta}(x)$ nahodilos' priblizhennoe reshenie $z_{\delta}(s)$ . Priblizhennoe reshenie $z_{\delta}(s)$ (tochki), predstavlennoe na ris. 1a, polucheno s pomosh'yu regulyariziruyushego algoritma, ispol'zuyushego apriornuyu informaciyu o vypuklosti iskomogo resheniya $z(s)$ . Pri popytke reshit' etu zhe zadachu bez regulyarizacii (ris. 1b) poluchayutsya skol' ugodno bol'shie otkloneniya "priblizhennogo resheniya" (tochki) ot istinnogo. Tak proyavlyaetsya nekorrektnost' obratnoi zadachi (2)

V nastoyashee vremya razvitaya teoriya resheniya nekorrektno postavlennyh zadach uspeshno primenyaetsya dlya resheniya mnogih obratnyh zadach astrofiziki, a takzhe zadach optiki i spektroskopii, optimal'nogo planirovaniya i t.p.

Vazhno otmetit', chto regulyariziruyushie algoritmy garantiruyut shodimost' posledovatel'nosti priblizhennyh reshenii k tochnomu resheniyu obratnoi zadachi, to est' pri stremlenii oshibki nablyudenii $\delta$ k nulyu priblizhennoe reshenie stremitsya k tochnomu. Eto daet veskie osnovaniya schitat', chto priblizhennoe reshenie nekorrektnoi zadachi, poluchennoe s pomosh'yu regulyariziruyushego algoritma, blizko k resheniyu, sootvetstvuyushemu ideal'no tochnym dannym nablyudenii u(x). Stihiinye intuitivnye metody resheniya obratnyh nekorrektnyh zadach, otmechennye vyshe, ne obladayut etim dostoinstvom.

V stat'e rassmotreny primery primeneniya regulyariziruyushih algoritmov k resheniyu obratnyh zadach astrofiziki.

Zvezdy vol'fa-raie v tesnyh dvoinyh sistemah

Zvezdy Vol'fa-Raie pervogo tipa naseleniya Galaktiki (to est' raspolozhennye vblizi galakticheskoi ploskosti) byli otkryty v 1867 godu francuzskimi uchenymi M. Vol'fom i Dzh. Raie. Sredi 100 mlrd zvezd Galaktiki takih zvezd izvestno okolo 200. Pochemu astronomy udelyayut stol' pristal'noe vnimanie izucheniyu etih ob'ektov? Delo v tom, chto v opticheskom spektre zvezd Vol'fa-Raie (WR) porazhaet odnovremennoe sushestvovanie sil'nyh i shirokih linii izlucheniya atomov i ionov vodoroda, geliya, a takzhe azota, ugleroda i kisloroda v raznyh stadiyah ionizacii (ris. 2).

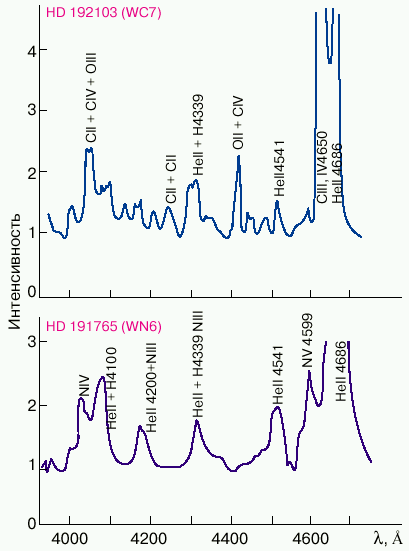Ris. 2. Opticheskie spektry dvuh zvezd Vol'fa-Raie: HD 191765 (WN6) i HD 192103 (WC7). Otmecheny linii izlucheniya razlichnyh himicheskih elementov

Dlya sushestvovaniya vysokoi stepeni ionizacii neobhodima temperatura v sotni tysyach gradusov, v to zhe vremya nepreryvnyi spektr zvezd WR v opticheskom diapazone grubo mozhet byt' approksimirovan izlucheniem absolyutno chernogo tela so srednei temperaturoi, ne prevyshayushei 10 000-20 000 K. Eto svidetel'stvuet o sil'nom otklonenii veshestva atmosfer zvezd WR ot sostoyaniya termodinamicheskogo ravnovesiya.

Zvezdy WR delyatsya na dve posledovatel'nosti: azotnuyu (WN) i uglerodnuyu (WC). V spektrah zvezd WN v osnovnom soderzhatsya linii azota, a v spektrah zvezd WC - linii ugleroda i kisloroda. I v zvezdah WN i v zvezdah WC prisutstvuyut linii geliya, a takzhe inogda slabye linii vodoroda. Ocenki otnositel'nogo soderzhaniya himicheskih elementov pokazyvayut, chto chislo atomov geliya v atmosferah zvezd WR vo mnogo raz bol'she, chem chislo atomov vodoroda. Etim zvezdy WR otlichayutsya ot obychnyh zvezd solnechnogo tipa. V poslednie gody vse bolee utverzhdaetsya tochka zreniya o tom, chto zvezdy WR predstavlyayut soboi obnazhennye yadra massivnyh m = 30-100 $M_{\odot}$ ( goryachih (T = 30 000-40 000 K) zvezd spektral'nyh klassov O ili B, poteryavshih znachitel'nuyu chast' (do 60%) svoei massy vsledstvie istecheniya veshestva libo v vide zvezdnogo vetra, libo v rezul'tate peretekaniya veshestva v tesnyh dvoinyh sistemah. Takim obrazom, skoree vsego, spektry zvezd WR demonstriruyut produkty termoyadernyh reakcii, protekayushih v nedrah massivnyh zvezd. Tem samym zvezdy WR kak by pozvolyayut zaglyanut' v laboratoriyu termoyadernogo sinteza himicheskih elementov, rabotayushuyu v nedrah massivnoi zvezdy!

Yavlyayas' ob'ektami absolyutno molodymi (vozrast ~ 10⁶ let), zvezdy WR, po-vidimomu, nahodyatsya na konechnoi stadii evolyucii: na stadii ischerpaniya zapasov yadernoi energii, posle kotoroi dolzhen sledovat' kollaps zvezdy s obrazovaniem relyativistskogo ob'ekta - neitronnoi zvezdy ili chernoi dyry. Kak vozmozhnye praroditeli neitronnyh zvezd i chernyh dyr zvezdy WR interesuyut mnogih issledovatelei. Odnako do poslednego vremeni problema zvezd WR byla daleka ot okonchatel'nogo resheniya. Naryadu s opisannoi koncepciei evolyucii zvezd WR sushestvuyut neskol'ko variantov dlya ob'yasneniya yavleniya WR. Ot gipotezy, v kotoroi zvezda WR schitaetsya molodym ob'ektom normal'nogo himicheskogo sostava, nahodyashimsya na stadii gravitacionnogo szhatiya, do modeli, soglasno kotoroi yavlenie WR v tesnyh dvoinyh sistemah svyazano so sverhkriticheskoi akkreciei na relyativistskii ob'ekt.

Takaya neodnoznachnost' v interpretacii yavleniya WR svyazana s tem, chto sobstvenno zvezda WR pogrebena vnutri moshnoi protyazhennoi atmosfery, radial'no rasshiryayusheisya pod deistviem davleniya radiacii so skorost'yu v tysyachi kilometrov v sekundu. Esli posmotret' na Solnce, to vidno, chto ego disk rezko ocherchen. Eto svyazano s tem, chto tolshina atmosfery Solnca, gde formiruetsya vidimoe izluchenie, sostavlyaet okolo 300 km, to est' poryadka odnoi desyatitysyachnoi ego radiusa. A u zvezdy WR atmosfera prostiraetsya na mnogo millionov kilometrov i v neskol'ko raz prevyshaet radius sobstvenno zvezdy. Pri etom massa atmosfery nichtozhno mala, v milliard raz men'she massy central'noi zvezdy. Situaciyu mozhno sravnit' s fonarem v tumane: razmery oreola gorazdo bol'she razmerov fonarya. Neudivitel'no poetomu, chto mnogie issledovateli, osnovyvayas' na izuchenii odinochnyh zvezd WR, kogda izmeryaetsya polnoe izluchenie ot vsego diska zvezdy s protyazhennoi atmosferoi, prihodili k vyvodu, chto radiusy zvezd WR veliki (poryadka 20-30 solnechnyh), a effektivnye temperatury otnositel'no nizki (poryadka 30 000 K).

S 1964 goda avtor nachal izuchat' zvezdy WR v zatmennyh dvoinyh sistemah. Kogda proishodit zatmenie zvezdy WR ee sputnikom - normal'noi zvezdoi spektral'nogo klassa OB s tonkoi atmosferoi, krivaya bleska soderzhit informaciyu ne tol'ko o summarnoi svetimosti zvezdy WR, no i o raspredelenii yarkosti po ee disku. Izvestno, chto dazhe v samyi krupnyi teleskop vse zvezdy (krome Solnca) vyglyadyat kak tochki. Iz-za kolossal'noi udalennosti zvezd WR ih diski nel'zya uvidet' (v otlichie ot Solnca, u kotorogo viden disk i mozhno izuchat' strukturu poverhnosti). Tem ne menee analiz zatmenii v dvoinyh sistemah, soderzhashih zvezdy WR, daet unikal'nuyu vozmozhnost' vosstanovit' raspredelenie yarkosti po disku zvezdy i tem samym kak by narisovat' ego izobrazhenie.

V obshem sluchae zadacha opredeleniya fizicheskih harakteristik zvezd iz analiza krivoi bleska zatmennoi dvoinoi sistemy svoditsya k resheniyu dvuh integral'nyh uravnenii Fredgol'ma 1-go roda

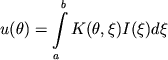
$u(\theta)=\int\limits_a^b K(\theta,\xi) I(\xi)d\xi$

(4)

i nelineinogo algebraicheskogo uravneniya, opisyvayushego blesk dvoinoi sistemy vne zatmenii. V uravnenii (4) funkciya $u(\theta)$ est' nablyudaemoe izmenenie bleska dvoinoi sistemy vo vremya zatmeniya, funkciya $K(\theta,\xi)$ - yadro uravneniya - takzhe izvestna: ona opisyvaet formu oblasti perekrytiya diskov komponent vo vremya zatmeniya ( $\theta$ - ugol otnositel'nogo povorota komponent na orbite, proporcional'nyi vremeni, $\xi$ - polyarnoe rasstoyanie na diske zvezdy WR). Zadacha resheniya integral'nogo uravneniya (4) predstavlyaet soboi tipichnuyu obratnuyu zadachu - po nablyudaemym sledstviyam processa zatmeniya - funkcii $u(\theta)$ (krivoi bleska) neobhodimo opredelit' raspredelenie yarkosti po disku zvezdy WR - funkciyu $I(\xi)$ . Eta zadacha otnositsya k klassu nekorrektno postavlennyh.

Klassicheskaya metodika interpretacii krivyh bleska zatmennyh dvoinyh zvezd osnovyvalas' na predpolozhenii o tom, chto tolshina atmosfery zvezdy mala po sravneniyu s ee radiusom. Teoriya tonkih zvezdnyh atmosfer daet analiticheskoe vyrazhenie dlya raspredeleniya yarkosti $I(\xi)$ kak funkciyu treh parametrov: yarkosti v centre diska zvezdy I₀ , radiusa zvezdy r i tak nazyvaemogo koefficienta potemneniya k krayu x. Analiticheskoe vyrazhenie dlya $I(\xi)$ podstavlyaetsya v uravnenie (4), kotoroe v rezul'tate integrirovaniya svoditsya k sisteme nelineinyh algebraicheskih uravnenii otnositel'no nebol'shogo chisla parametrov. Eto pozvolyaet oboiti trudnosti, svyazannye s nekorrektnost'yu obratnoi zadachi (4).

U zvezd WR protyazhennye atmosfery. Slozhnost' fizicheskih processov i neopredelennost' modelei protyazhennyh zvezdnyh atmosfer ne pozvolyayut primenit' v dannom sluchae klassicheskii sposob parametrizacii iskomoi funkcii $I(\xi)$ pri reshenii obratnoi zadachi(4) . Vmeste s tem o funkcii $I(\xi)$ v dannom sluchae imeetsya estestvennaya apriornaya informaciya kachestvennogo haraktera: ee mozhno schitat' monotonnoi i neotricatel'noi. Kak dokazano sotrudnikami kafedry matematiki fizicheskogo fakul'teta MGU A.V. Goncharskim i A.G. Yagoloi, algoritm resheniya obratnoi zadachi (4) na mnozhestve monotonnyh neotricatel'nyh funkcii yavlyaetsya regulyariziruyushim, a sama zadacha (4) na etom mnozhestve funkcii I(x) yavlyaetsya korrektnoi v klassicheskom smysle. Eto pozvolilo po-novomu postavit' zadachu interpretacii krivyh bleska zatmennyh dvoinyh sistem i na osnove sovremennyh metodov regulyarizacii nekorrektno postavlennyh zadach razrabotat' effektivnye chislennye algoritmy ee resheniya dlya komp'yuterov. Nekorrektnost' zadachi (4) byla preodolena, i polucheno ee ustoichivoe reshenie. Eto stimulirovalo nablyudeniya vseh izvestnyh zatmennyh dvoinyh zvezd s komponentami WR, a poluchennye nablyudatel'nye dannye v ul'trafioletovom, opticheskom i infrakrasnom diapazonah interpretirovalis' s pomosh'yu novoi metodiki.

V rezul'tate resheniya obratnoi zadachi interpretacii krivyh bleska zatmennyh dvoinyh zvezd okazalos' vozmozhnym vosstanovit' raspredelenie yarkosti po disku zvezdy WR v razlichnyh uchastkah spektra (ris. 3), otdelit' izluchenie sobstvenno zvezdy WR ot izlucheniya ee protyazhennoi atmosfery i tem samym opredelit' istinnyi radius, temperaturu i svetimost' zvezdy WR.

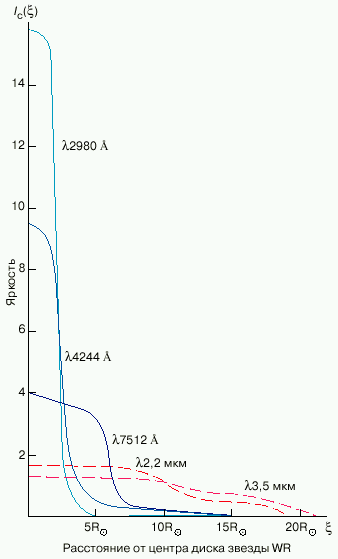Ris. 3. Raspredelenie yarkosti po disku zvezdy WN5 v zatmennoi dvoinoi sisteme V444 Lebedya, vosstanovlennoe po krivym bleska v raznyh oblastyah spektra na mnozhestve monotonnyh neotricatel'nyh funkcii. Hotya polnyi radius protyazhennoi atmosfery zvezdy WN5 sostavlyaet okolo 20 solnechnyh, radius sobstvenno zvezdy WR (opredelyaemyi po shirine central'nogo maksimuma intensivnosti v sinei oblasti spektra) ne prevyshaet 3 solnechnyh, a ego temperatura bolee 50 000 K

Okazalos', chto, v to vremya kak polnyi radius vidimoi atmosfery zvezdy WR sostavlyaet ~ 20 solnechnyh, radius sobstvenno zvezdy WR (to est' gidrostaticheskogo tela zvezdy, soderzhashego osnovnuyu chast' massy) sostavlyaet vsego lish' okolo 3 solnechnyh, a temperatura sobstvenno zvezdy WR prevyshaet 50 000 K (!). Otnositel'no nizkaya temperatura izlucheniya vsego diska zvezdy WR (~ 20 000 K) svyazana s nizkotemperaturnym rekombinacionnym izlucheniem poluprozrachnoi protyazhennoi atmosfery, vklad kotoroi v vidimoi oblasti spektra dostigaet 80%. Malyi radius zvezdy WR i vysokaya effektivnaya temperatura pri masse 10 solnechnyh svidetel'stvuyut o tom, chto zvezda WR yavlyaetsya gelievym ostatkom ot pervonachal'no massivnoi zvezdy, poteryavshei osnovnuyu chast' vodorodnoi obolochki. Nash vyvod o malyh radiusah i vysokih temperaturah zvezd WR v poslednee vremya podtverzhden nezavisimym analizom dannyh polyarizacionnyh nablyudenii zatmennyh dvoinyh zvezd WR (A. Moffat, Kanada), a takzhe otkrytiem gollandskoi gruppoi (Van Kerkvik i dr.) zvezdy Vol'fa-Raie v ochen' korotkoperiodicheskoi rentgenovskoi dvoinoi sisteme Lebed' X-3, soderzhashei akkreciruyushii relyativistskii ob'ekt.

Analiz difrakcionnyh krivyh bleska pri pokrytii zvezd lunoi

Pri nablyudeniyah nebesnyh tel astronomy vsegda stremyatsya dostich' kak mozhno bolee vysokogo uglovogo razresheniya. Chtoby dobit'sya etogo, oni idut na hitroumnye i podchas ves'ma dorogostoyashie uhishreniya. Sozdayutsya interferometry raznyh tipov, zapuskayutsya teleskopy za predely iskazhayushei zemnoi atmosfery (naprimer, izvestnyi kosmicheskii teleskop im. Habbla s zerkalom diametrom 2,4 m). Odnako okazyvaetsya, chto vysokoe uglovoe razreshenie (do 10^{- 3}-10^{- 4} sekundy dugi) mozhno poluchit' gorazdo bolee prostym i deshevym sposobom, nablyudaya pokrytiya zvezd Lunoi s pomosh'yu nazemnyh teleskopov so skromnym diametrom poryadka 1 m. Sut' metoda prosta: Luna pri orbital'nom dvizhenii vokrug Zemli zatmevaet zvezdy. Uglovye diametry sravnitel'no blizkih zvezd sostavlyayut neskol'ko tysyachnyh sekundy dugi. Tol'ko u nekotoryh samyh blizkih zvezd - gigantov i sverhgigantov uglovye razmery dostigayut sotyh dolei sekundy. Yasno, chto process zatmeniya diska zvezdy Lunoi budet imet' hotya i ochen' maluyu, no vpolne izmerimuyu prodolzhitel'nost' - poryadka neskol'kih sotyh sekundy vremeni. Sledovatel'no, provedya vysokotochnye fotoelektricheskie nablyudeniya s dostatochno vysokim vremennym razresheniem (okolo 10^{- 3} s), mozhno poluchit' krivuyu zatmeniya zvezdy Lunoi, kotoraya budet obuslovlena kak geometricheskim zatmeniem, tak i effektami difrakcii sveta zvezdy na krayu diska Luny (ris. 4).

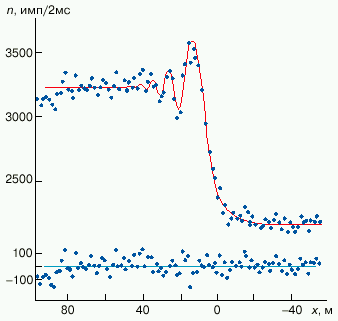Ris. 4. Nablyudaemaya (tochki) i teoreticheskaya krivye bleska pri zatmenii Lunoi zvezdy 61 $\delta$ ' v sozvezdii Tel'ca. Po osi absciss otlozheno rasstoyanie ot kraya Luny do proekcii centra diska zvezdy na ploskost' lunnogo diska. Po osi ordinat otlozhena intensivnost' v uslovnyh edinicah. Viden effekt difrakcii sveta zvezdy na krayu diska Luny, proyavlyayushiisya v cheredovanii maksimumov i minimumov intensivnosti izlucheniya pered vhodom v zatmenie. Vysota difrakcionnyh maksimumov tem men'she, chem bol'she uglovoi diametr zvezdy. Reshenie obratnoi zadachi interpretacii krivoi bleska na mnozhestve konechno-parametricheskih funkcii daet dlya uglovogo diametra zvezdy znachenie 0,"0028 s neopredelennost'yu v 0,"001. Vnizu pokazany ostatochnye ukloneniya nablyudennyh tochek ot model'noi teoreticheskoi krivoi

Chem bol'she uglovoi diametr zatmevaemoi zvezdy, tem men'she budet vysota difrakcionnyh maksimumov i tem blizhe krivaya bleska pri pokrytii zvezdy Lunoi budet napominat' krivuyu geometricheskogo zatmeniya. Takim obrazom, reshaya obratnuyu zadachu interpretacii krivoi pokrytiya zvezdy Lunoi, mozhno opredelit' uglovoi diametr zvezdy i dazhe pytat'sya poluchat' informaciyu o raspredelenii yarkosti po disku zvezdy ili o nalichii okolozvezdnoi struktury (naprimer, protoplanetnogo diska vokrug zvezdy, ee blizkogo sputnika i t.p.). Vazhno to, chto i Luna i zatmevaemaya eyu zvezda nahodyatsya za predelami nespokoinoi zemnoi atmosfery, poetomu atmosfernye iskazheniya ne mogut sushestvenno povliyat' na vid difrakcionnoi krivoi pokrytiya zvezdy Lunoi.

Matematicheski rassmatrivaemaya zadacha zaklyuchaetsya v reshenii integral'nogo uravneniya Fredgol'ma 1-go roda

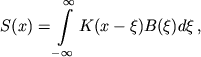
$S(x)=\int\limits_{-\infty}^{\infty} K(x-\xi)B(\xi)d\xi\,,$

(5)

gde S(x) - nablyudaemaya difrakcionnaya kartina izmeneniya intensivnosti pri pokrytii zvezdy Lunoi, x(t) = V(t - t₀), V - proekciya lineinoi skorosti dvizheniya lunnogo kraya na ego normal' v napravlenii na proekciyu zvezdy, t - vremya, t ₀ - moment vremeni, kogda centr zvezdy tochno proektiruetsya na krai lunnogo diska, $B(\xi)$ - iskomaya funkciya, vyrazhayushaya strip-raspredelenie yarkosti po disku zvezdy (to est' raspredelenie, prointegrirovannoe vdol' pryamyh, parallel'nyh lunnomu krayu). Yadro $K(x-\xi)$ predstavlyaet soboi difrakcionnuyu kartinu tochechnogo istochnika, poluchennuyu s uchetom vliyaniya razlichnyh iskazhayushih faktorov (otlichie ot nulya ekspozicii izmerenii, nemonohromatichnost' registriruemogo svetovogo potoka, otlichnyi ot nulya diametr teleskopa i t.p.). Yadro $K(x-\xi)$ vyrazhaetsya cherez integraly Frenelya, opisyvayushie difrakciyu izlucheniya beskonechno udalennogo tochechnogo monohromaticheskogo istochnika na krayu beskonechnogo ploskogo ekrana.

Uravnenie (5) - integral'noe uravnenie Fredgol'ma 1-go roda, kotoroe nuzhno reshat' s pomosh'yu metoda regulyarizacii. Estestvennoi apriornoi informaciei ob iskomoi funkcii yavlyaetsya ee monotonnost' ili vypuklost', a takzhe neotricatel'nost'. Krome togo, v sluchae zvezdy s tonkoi atmosferoi mozhno ispol'zovat' analiticheskoe konechno-parametricheskoe predstavlenie funkcii $B(\xi)$ , poluchennoe iz teorii. V sluchae, esli nablyudaetsya pokrytie dvoinoi zvezdy ili zvezdy, obladayushei okolozvezdnoi strukturoi, mozhno ispol'zovat' regulyariziruyushii algoritm Tihonova na mnozhestve gladkih neotricatel'nyh funkcii.

Na ris. 4 privedeny nablyudaemaya i teoreticheskaya krivye bleska pri pokrytii zvezdy 61 $\delta$ ' Tel'ca (giganta spektral'nogo klassa K0) Lunoi. Nablyudeniya vypolneny na avtomatizirovannoi sisteme teleskop+komp'yuter Alma-Atinskoi vysokogornoi observatorii GAISh s vremennym razresheniem 10^{- 3} s. Naidennyi takim obrazom uglovoi diametr zvezdy 61 $\delta$ ' Tel'ca sostavlyaet d = 0,"0028 $\pm$ 0,"0010.

Primenenie metoda nablyudenii pokrytii zvezd Lunoi k issledovaniyu molodyh zvezd tipa T Tel'ca pozvolilo vyyavit' vnutrennie chasti okolozvezdnogo (protoplanetnogo?) diska vokrug zvezdy DG v sozvezdii Tel'ca s uglovym razresheniem do 10^-4 sekundy dugi (ris. 5).

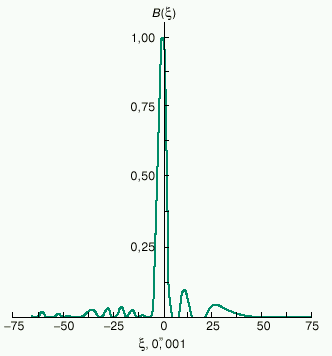Ris. 5. Strip-raspredelenie yarkosti $B(\xi)$ dlya zvezdy DG v sozvezdii Tel'ca, vosstanovlennoe nami sovmestno s M.B. Bogdanovym iz difrakcionnoi krivoi pokrytiya Lunoi, poluchennoi A. Rikiki (Italiya). Ispol'zovalsya metod regulyarizacii na mnozhestve gladkih neotricatel'nyh funkcii. Central'nyi pik sootvetstvuet zvezde. Slozhnaya struktura v kryl'yah, proslezhivaemaya do rasstoyaniya v tri rasstoyaniya ot Zemli do Solnca ot centra zvezdy, sootvetstvuet central'nym chastyam protoplanetnogo diska vokrug zvezdy

K nastoyashemu vremeni metodom lunnyh pokrytii opredeleny uglovye diametry soten zvezd, otkryty tysyachi novyh tesnyh dvoinyh zvezd, izuchena struktura protoplanetnyh diskov vokrug molodyh zvezd. Takim obrazom, metod lunnyh pokrytii prevratilsya v moshnyi metod issledovaniya zvezd s ochen' vysokim uglovym razresheniem (do 10^{- 4} sekundy dugi).

Zaklyuchenie

Na primere dvuh obratnyh zadach astrofiziki my pokazali, kak sovremennyi matematicheskii apparat, primenennyi k analizu vysokotochnoi nablyudatel'noi informacii, pozvolyaet delat' vazhnye vyvody o prirode i evolyucii razlichnyh astrofizicheskih ob'ektov, udalennyh ot nas na gromadnye rasstoyaniya.

Za neimeniem mesta my ne smogli opisat' drugie obratnye zadachi astrofiziki, takie, kak vosstanovlenie raspredeleniya himicheskih elementov po poverhnostyam pekulyarnyh Ap-zvezd po peremennosti linii poglosheniya v ih spektrah, vosstanovlenie radioastronomicheskih i opticheskih izobrazhenii nebesnyh tel iz nablyudenii, iskazhennyh vliyaniem apparatnoi funkcii, povyshenie razreshayushei sposobnosti spektrografa i mnogie drugie obratnye zadachi. Vo vseh etih zadachah primenenie sovremennyh regulyariziruyushih algoritmov okazalos' effektivnym.

Otmetim, chto v stat'e my podrobno ostanovilis' lish' na metodah resheniya obratnyh zadach v determinirovannoi postanovke, kogda ispol'zuetsya ponyatie absolyutnoi oshibki nablyudatel'nyh dannyh $\delta$ . Metody resheniya obratnyh zadach v statisticheskoi postanovke, osnovannye na informacionnom podhode, v tom ili inom vide takzhe ispol'zuyut apriornuyu informaciyu ob iskomom reshenii i osobenno polezny pri vosstanovlenii izobrazhenii astronomicheskih ob'ektov, gde estestvennoi apriornoi informaciei yavlyaetsya informaciya o neotricatel'nosti iskomoi funkcii.

Literatura


[1]	Goncharskii A.V., Cherepashuk A.M., Yagola A.G. Chislennye metody resheniya obratnyh zadach astrofiziki. M.: Nauka, 1978.
[2]	Goncharskii A.V., Cherepashuk A.M., Yagola A.G. Nekorrektnye zadachi astrofiziki. M.: Nauka, 1985.
[3]	Goncharskii A.V., Cherepashuk A.M., Yagola A.G. Nekorrektnye zadachi v sovremennoi astrofizike // Priroda. 1985. No 9. S. 3-16.
[4]	Bogdanov M.B., Trunkovskii E.M., Cherepashuk A.M. Sistema "Zemlya-Luna" kak teleskop sverhvysokogo razresheniya // Zemlya i Vselennaya. 1992. No 6. S. 3-11.

Publikacii s klyuchevymi slovami: obrabotka nablyudenii - nekorrektnye zadachi - dvoinye zvezdy Publikacii so slovami: obrabotka nablyudenii - nekorrektnye zadachi - dvoinye zvezdy
Sm. takzhe: BHB2007: formirovanie dvoinoi zvezdy Propavshaya zvezda-kompan'on sverhnovoi Issledovanie, kotoroe mozhet povtorit' lyuboi pol'zovatel' Interneta Tumannost' Ozherel'e Krasnaya pryamougol'naya tumannost' Taina umirayushei zvezdy Rassvet pered vzryvom novoi zvezdy Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce