Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Vzaimodeistvie kosmicheskih tel s atmosferami Zemli i planet

G.A.TIRSKI'

Moskovskii fiziko-tehnicheskii institut, Dolgoprudnyi Moskovskoi obl.

Kachestvenno i kolichestvenno rassmotreno vzaimodeistvie kosmicheskih tel – meteoroidov, dvizhushihsya s meteornymi skorostyami (ot 11 do 72 km/s), s atmosferami Zemli i planet. Privodyatsya kolichestvennaya teoriya tormozheniya, poteri kineticheskoi energii i nachala drobleniya meteoroidov. Daetsya ob'yasnenie yavleniyu "vzryva" kosmicheskih tel v atmosfere planety.

S neba upala zvezda,
Vidish', letit nad toboi!
Drug moi, ona nikogda
Ne byla tam zvezdoi.
Slushai nebesnuyu byl',
Tainu dalekih mirov -
Eto mezhzvezdnaya pyl',
Inei kometnyh mirov.
Nikolai Morozov
"Zvezdnye pesni"

Vvedenie

Ezhednevno v atmosferu Zemli vletayut s meteornymi skorostyami (bolee 11,2 km/s) okolo 70 mln kosmicheskih tel – tverdyh ob'ektov razmerom primerno ot 5 x 10-6 sm i bolee – meteoroidov, intensivno vzaimodeistvuyushih s nei [1]. Malye tela razmerom do 10-2 sm porozhdayut yavlenie meteora ("padayushei zvezdy"), to est' sozdayut pri bystrom dvizhenii v atmosfere dostatochno sil'noe svechenie i ionizacionnyi sled takoi intensivnosti, chto stanovitsya vozmozhnym ih nablyudenie vizual'nym, fotograficheskim ili radiolokacionnym metodami.

Meteoroidy vletayut v atmosferu Zemli so skorostyami ot 11,2 do $\sim$72 km/s v lyubom napravlenii, v lyuboe vremya sutok i goda i v lyubom meste zemnogo shara, poyavlyayutsya vsegda neozhidanno, i nel'zya zaranee predskazat', gde i kogda oni upadut i voobshe doletyat li oni do Zemli i prevratyatsya li v meteority.

Slovo "meteoron" v perevode s grecheskogo oznachaet "yavlenie". Na francuzskom yazyke slovo "meteor" oznachaet ne tol'ko padayushuyu zvezdu, no takzhe radugu, galo, molniyu, nekotorye vidy osadkov. Nauka o yavleniyah v atmosfere poetomu i nazyvaetsya meteorologiei.

Atmosfera yavlyaetsya gazovym shitom i separatorom pronikayushih k poverhnosti planety kosmicheskih tel. Poetomu iz etogo bol'shogo kolichestva kosmicheskih prishel'cev vyzhivaet posle ves'ma intensivnogo kombinirovannogo konvektivno-radiacionnogo nagreva (i kak sledstvie – ih plavleniya i ispareniya), a takzhe vsledstvie bol'shih peregruzok (dostigayushih neskol'kih tysyach g), privodyashih k ih mehanicheskomu razrusheniyu i dal'neishemu (na poslednem etape) bystromu plavleniyu i ispareniyu dopolnitel'no razdroblennyh za schet termonapryazhenii melkih kuskov, tol'ko, veroyatno, okolo 1000 kg (1%) meteornogo materiala i dostigaet poverhnosti Zemli v vide otdel'nyh (makro-)fragmentov – meteoritov [1].

Posle padeniya krupneishih iz nih na Zemlyu obrazuyutsya kratery, a na more ili okeane – bol'shie volny i cunami (cunami – yaponskoe nazvanie morskih voln, voznikayushih ot podvodnyh zemletryasenii, a takzhe inogda pri vzryvnyh izverzheniyah podvodnyh ili ostrovnyh vulkanov). Ocenki ezhesutochnogo privnosa kosmicheskoi materii na Zemlyu, poluchennye s pomosh'yu razlichnyh metodik, razlichayutsya primerno na chetyre poryadka velichiny, no bol'shinstvo iz nih popadayut v interval ot 100 do 1000 t v den' [2].

Takim obrazom, ezhesutochno na poverhnost' Zemli bolee ili menee ravnomerno vysypaetsya s raznymi skorostyami neskol'ko desyatkov samosvalov kosmicheskoi pyli, peska, graviya i bulyzhnikov (teplyh i goryachih), sozdayushih pered etim v nebe zahvatyvayushee prirodnoe yavlenie, soprovozhdaemoe effektivnymi svetovymi, zvukovymi i dazhe vzryvnymi yavleniyami. U naibolee krupnyh ekzemplyarov (bolee 1 kg), obrazuyushih yavlenie bolida (ot grech. "bolidos" – metatel'noe kop'e), vidimyi poperechnik dostigaet i dazhe prevoshodit vidimyi diametr polnoi Luny ili Solnca. Za bolidom tyanetsya ognennyi hvost i s treskom syplyutsya iskry. V celom zhe massa Zemli ot takogo ne prekrashayushegosya ni dnem ni noch'yu meteornogo "dusha" uvelichivaetsya za god primerno na 107 t. Hotya eta velichina i predstavlyaetsya vnushitel'noi, massa Zemli pri etom uvelichivaetsya vsego primerno na 4 x 10-6 % za 1 mlrd let.

Izucheniem meteornyh yavlenii zanimayutsya issledovateli ves'ma shirokogo kruga special'nostei: astronomy, specialisty po giperzvukovoi aerodinamike, teplo- i massoobmenu, molekulyarnoi fizike, radiofizike, spektroskopii, plazme, geologii i dr. Issledovanie meteorov i meteoritov (mirovye kollekcii naschityvayut seichas ne menee 2000 vidov meteoritov) prinosit uchenym cennye svedeniya o veshestve kosmicheskogo prostranstva (eti tela prihodyat k nam poroi iz chrezvychaino udalennyh oblastei Solnechnoi sistemy). Ponimanie processov vzaimodeistviya krupnyh kosmicheskih tel s atmosferami planet tesno svyazano s teoriei obrazovaniya kraterov na planete; eto ponimanie vazhno takzhe dlya pravil'noi interpretacii razlichnyh nablyudenii v atmosfere. Sputniki s pomosh'yu opticheskoi apparatury dovol'no chasto registriruyut yarkie vspyshki v atmosfere Zemli na vysotah 20-40 km.

V poslednee vremya vyskazyvaetsya mnenie, chto proishozhdenie zhizni na Zemle svyazano s organicheskoi materiei, zanesennoi na Zemlyu padayushimi meteoritami [3], a takzhe ostro obsuzhdaetsya problema asteroidnoi opasnosti dlya Zemli – padeniya na Zemlyu krupnyh kosmicheskih tel s regional'nymi i dazhe global'nymi katastroficheskimi posledstviyami.

I segodnya eshe ne utihayut diskussii po povodu ob'yasneniya Tungusskogo sobytiya [4] – padeniya oskolka ili yadra komety na Zemlyu (1908 god), ostavivshego v meste padeniya zametnoe kolichestvo melkogo (menee 200 mkm) meteornogo veshestva i ogromnyi vyval chastichno obgorevshego (v epicentre) lesa v sibirskoi taige na ploshadi 2000 km2. Krater v meste padeniya Tungusskogo tela ne obnaruzhen, hotya mesto padeniya issleduetsya s 20-h godov. Vse eto govorit o slozhnom mnogoaktovom scenarii vzaimodeistviya krupnyh kosmicheskih tel s atmosferami planet, kotoryi v nastoyashee vremya ponyat uchenymi kachestvenno, no kolichestvenno do konca ne izuchen.

V rabote izlagayutsya kachestvenno i kolichestvenno nekotorye aspekty, naskol'ko eto mozhno sdelat' v kratkoi stat'e, vzaimodeistviya vletayushih s giperzvukovoi skorost'yu tel s atmosferoi planety. Snachala privedem osnovnye opredelyayushie parametry meteornyh yavlenii.

Massy, razmery

V shkale mass meteoroidy ohvatyvayut diapazon ot 10-7 do 107 g, vklyuchaya tela, porozhdayushie naibolee yarkie bolidy. Odnako takoi meteoroid, kak Tungusskii (okolo 2 x 106 t), rasshiryaet diapazon mass vozmozhnyh meteornyh tel do 1012 g, a oskolki komety Shumeikerov–Levi 9, vletevshie v atmosferu Yupitera v iyule 1994 goda, uvelichivayut etot diapazon do 1016–1017 g. Krome togo, termoeroziya meteornyh tel v verhnih sloyah atmosfery s obrazovaniem pylevyh hvostov za nimi, a takzhe prisutstvie ves'ma melkih kosmicheskih chastic razmerom menee 10-2 sm, vletayushih i bystro tormozyashihsya v verhnih sloyah atmosfery (dlya Zemli na vysote bolee 100 km) s ves'ma maloi poterei massy i zatem osedayushih pod deistviem sily tyazhesti na poverhnost' Zemli (primerno v techenie do dvuh let), zastavlyayut issledovatelei rassmatrivat' chastichki s massoi menee 10-6–10-7 g. Bolee togo, ispol'zovanie dannyh schetchikov meteornyh chastic na raketah i sputnikah, analiz mikrokraterov na poverhnosti Luny, nablyudenie serebristyh oblakov dovodyat nizhnii predel mass do 10-13–10-12 g. Malye chasticy s verhnim predelom mass, ravnym 10-6 g, nazyvayutsya mikrometeoroidami. Razmer etih chastic nastol'ko mal, chto, kak my uvidim dalee, oni tormozyatsya v verhnih sloyah atmosfery ran'she, chem nagreyutsya do temperatury ispareniya i smogut nachat' svetit'sya. Massa v 10-6 g primerno sootvetstvuet nizhnemu predelu mass chastic, polet kotoryh registriruetsya naibolee chuvstvitel'nymi radiolokatorami. Razmery etih chastic 0,1 mm i menee. Takim obrazom, diapazon mass meteoroidov, real'no nablyudavshihsya v atmosferah planet Solnechnoi sistemy, ohvatyvaet okolo 30 poryadkov! Odnako bol'shaya chast' vnezemnogo veshestva, priletayushego iz kosmicheskogo prostranstva, sostoit iz tel s massoi menee 100 g. Esli prinyat' nizhnyuyu granicu plotnosti ravnoi plotnosti vodyanogo l'da $\delta$ = 1 g/sm3, to razmery meteoroidov v poperechnike budut menyat'sya ot 10-4 sm do 10 km. Na samom dele nizhnii predel mozhno umen'shit' primerno do 5 x 10-6 sm. Etot predel nemnogo perekryvaetsya s kolloidnym diapazonom.

Skorosti, ugly vhoda

Zemlya obrashaetsya po svoei orbite vokrug Solnca so srednei skorost'yu (orbital'naya skorost') 29,8 km/s, i ona dvizhetsya navstrechu odnim kosmicheskim telam i ubegaet ot drugih. Minimal'naya skorost' dogonyayushego ili dogonyaemogo kosmicheskogo tela otnositel'no planety ravna vtoroi kosmicheskoi skorosti VII=$\sqrt{2}$VI, gde VI – pervaya kosmicheskaya skorost', sootvetstvuyushaya minimumu neobhodimoi energii vyvedeniya tela (sputnika) na krugovuyu orbitu planety i priblizhenno ravnaya VI = $\sqrt{Rg\,}$, gde R – radius planety, g – uskorenie sily tyazhesti. Dlya Zemli VI = 7,9 km/s, VII = 11,2 km/s. Maksimal'naya skorost' kosmicheskogo tela, razognannogo iz sostoyaniya pokoya pod deistviem prityazheniya Solnca (parabolicheskaya skorost' na rasstoyanii Zemli), ravna 42,2 km/s. Takim obrazom, esli priderzhivat'sya ustanovivsheisya tochki zreniya, chto meteornye tela imeyut solnechnoe proishozhdenie, diapazon skorostei vhoda meteoroidov v atmosferu Zemli budet ot 11 km/s, esli meteoroid dogonyaet Zemlyu s minimal'noi skorost'yu i ne uchityvaetsya prityazhenie Zemli, do 72 km/s (meteoroid vstrechaet Zemlyu s parabolicheskoi skorost'yu so storony apeksa – tochki na nebe, ukazyvayushei napravlenie dvizheniya Zemli vokrug Solnca). Skorost' vhoda mikrometeoroidov za schet dopolnitel'nogo effekta prityazheniya Zemli mozhet byt' i neskol'ko bol'she 72 km/s i dostigat' 72,8 km/s. Meteornyi potok Leonidov v noyabre 1998 goda vletal v atmosferu Zemli so skorost'yu do 74 km/s. V tabl. 1 privedeny harakternye skorosti dlya planet i diapazon skorostei vhoda kosmicheskih tel v atmosfery planet (VII-Vmax).

Tablica 1

PlanetyVorb, km/sVI, km/sVII, km/s VII-Vmax, km/sh, km
Venera 35,00 7,25 10,25 10,25-84,5 6,2
Zemlya 29,77 7,91 11,19 11,19-72,8 6,7
Mars 24,22 3,57 5,09 5,19-58,2 28
Yupiter 13,07 42,2 60,20 60,20-68,0 18
Saturn 9,65 25,1 36,20 36,20-42,8 19

Ugol vhoda meteornyh tel v atmosferu Zemli izmenyaetsya ot 90° (vertikal'nyi vhod) do ves'ma malyh znachenii. Odnako bol'shinstvo nablyudaemyh meteorov vhodit v atmosferu pod dovol'no bol'shimi uglami.

Sostav i plotnost' meteoroidov

Meteority, naidennye na poverhnosti Zemli, kotorye imeyut asteroidnoe i, vozmozhno, kometnoe proishozhdenie, po sostavu delyatsya na tri osnovnyh klassa – zheleznye, zhelezokamennye i kamennye – v zavisimosti ot sootnosheniya v nih silikatnyh mineralov i nikelistovogo zheleza. Naibolee redko padayut zhelezokamennye meteority: oni padayut raz v sem'desyat rezhe, chem kamennye. Himicheskie analizy meteoritov pokazali, chto vse oni sostoyat iz teh zhe himicheskih elementov, chto i zemnye ob'ekty. Nikakih novyh himicheskih elementov v nih ne obnaruzheno. Plotnost' zheleznyh meteoritov $\delta$= 7,6 g/sm3, kamennyh $\delta \simeq$ 3,5 g/sm3, ryhlyh kamennyh $\delta \simeq$ 2,2 g/sm3.

Kamennye meteority sostavlyayut bol'shinstvo (93%) padenii na Zemlyu, ostal'noe – zheleznye i zhelezokamennye.

Po sovremennym vozzreniyam, znachitel'naya chast' vletayushih v zemnuyu atmosferu melkih meteornyh chastic, porozhdayushih yavlenie meteora, yavlyaetsya produktom razrusheniya komet, "ineem" komet, kak skazal v svoem stihotvorenii revolyucioner-shlissel'burzhec N.A. Morozov eshe v nachale etogo stoletiya.

Atmosfera

Ballistika meteoroida sushestvenno zavisit ot svoistv (v pervuyu ochered' ot plotnosti) atmosfery planety, tak kak tormozhenie meteoroida mozhno rassmotrivat' kak rastyanutyi vo vremeni "udar" tela ob atmosferu .

Izmenenie temperatury atmosfery Zemli po vysote obychno ne prevoshodit 50–60 K (nizhe primerno 100 km), chto blizko k temperaturnym kolebaniyam u zemnoi poverhnosti. Poetomu v pervom priblizhenii, vpolne dostatochnom dlya mnogih celei meteornoi astronomii, mozhno prinyat' atmosferu Zemli (kak, vprochem, i drugih planet) izotermicheskoi. Togda iz uravneniya sostoyaniya p = $\rho$RT / m i uravneniya gidrostaticheskogo ravnovesiya atmosfery $\rho$g = - dp / dz poluchaem eksponencial'noe raspredelenie plotnosti po vysote z:

$$\rho=\rho_0 \exp(-z/h), \qquad h=R_AT/(mg)\,,$$ (1)

gde $p$ - davlenie, $\rho$ - plotnost', $R_A$ - absolyutnaya gazovaya postoyannaya, $T$ - temperatura, $m$ - srednyaya molekulyarnaya massa atmosfery, $g$ - uskorenie sily tyazhesti, $\rho_{0}$ - uslovnaya plotnost' atmosfery na poverhnosti Zemli ($\rho_{0}$ = 0,001750 g/sm3).

Velichina $h$ nazyvaetsya shkaloi vysot i dlya Zemli ravna 6,7 km. V tabl. 1 privedeny srednie velichiny $h$ dlya ryada planet.

Ballistika ideal'nogo meteoroida

Prezhde chem govorit' o real'nom vzaimodeistvii meteoroida s atmosferoi planety, rassmotrim idealizirovannuyu zadachu ballistiki o vhode s bol'shoi skorost'yu absolyutno tverdogo (nedeformiruemogo) adiabaticheskogo (teploizolirovannogo) tela, to est' tela, kotoroe nechuvstvitel'no k posledstviyam peregruzki (tormozheniyu) i ne podverzheno aerodinamicheskomu nagrevaniyu, plavleniyu, ispareniyu, termonapryazheniyam, termomehanicheskoi erozii i t.p., to est' ono sohranyaet v processe dvizheniya skvoz' atmosferu svoyu massu i temperaturu dalekogo kosmosa, ravnuyu ravnovesnoi temperature chernogo tela T0 = 280 K na rasstoyanii 1 a.e. ($\sim$150 mln km) ot Solnca. Takoe telo budem nazyvat' ideal'nym meteoroidom (IM). Rassmotrenie dinamiki IM vazhno po krainei mere s treh tochek zreniya. Vo-pervyh, ballistika IM poddaetsya polnomu i prostomu matematicheskomu analizu v analiticheskom vide. Vo-vtoryh, mnogie kachestvennye i otchasti kolichestvennye vyvody teorii IM ostayutsya vernymi i pri real'nom vzaimodeistvii ochen' melkih (R < 10-2 sm) i ochen' krupnyh (R > 103 sm) meteoroidov s atmosferoi planety do nachala ih mehanicheskogo razrusheniya pod deistviem massovyh sil inercii i aerodinamicheskih poverhnostnyh sil. V-tret'ih, opredelyaemye parametry vzaimodeistviya (maksimal'noe tormozhenie, maksimal'naya poterya kineticheskoi energii i dr.) IM budut opornymi parametrami dlya oblegcheniya interpretacii real'nogo vzaimodeistviya meteoroida s atmosferoi.

Dvizhenie centra mass tela neizmennoi massy i ploshad'yu poperechnogo secheniya (midelya – ot gol. middel, angl. middle) A, dvizhushegosya so skorost'yu $\upsilon$ v srede s plotnost'yu $\rho$, podchinyaetsya vtoromu zakonu N'yutona (massa m, umnozhennaya na uskorenie d$\upsilon$ / dt, ravna prilozhennoi sile):

$$m\frac{d\upsilon}{dt}=-\frac{1}{2}AC_D\rho\upsilon^2\,.$$ (2)

V etom uravnenii CD - bezrazmernyi koefficient soprotivleniya, harakterizuyushii dolyu plotnosti potoka impul'sa (kolichestva dvizheniya) $\rho\upsilon^{2}$ nabegayushego na telo potoka, peredavaemogo telu. Pri dvizhenii v sil'no razrezhennom gaze, kogda dlina svobodnogo probega molekul bol'she harakternogo razmera tela, CD = 2, to est' ves' impul's nabegayushego gaza peredaetsya telu (neuprugii udar molekul). Pri dvizhenii tela v dostatochno plotnoi atmosfere, kogda dlina svobodnogo probega molekul mnogo men'she harakternogo razmera tela, dlya vypuklyh gladkih tel, blizkih k sfere, pri meteornyh skorostyah CD $\approx$ 1. Na ris. 1 eti oblasti razgranicheny shtrihovoi liniei.

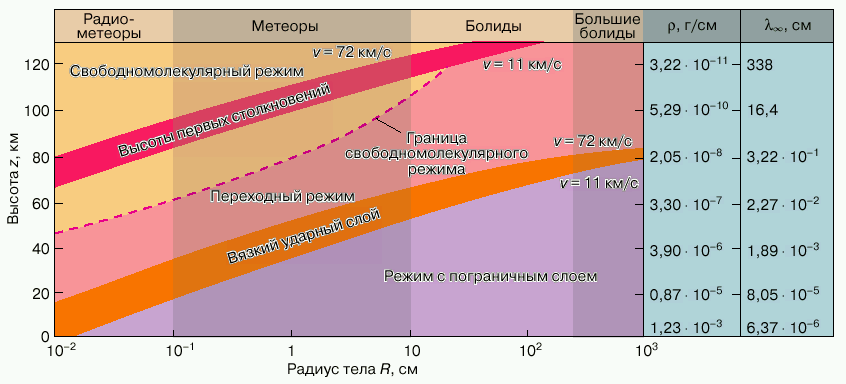Ris. 1. Rezhimy obtekaniya tel raznyh razmerov pri vhode v atmosferu Zemli s meteornymi skorostyami. Sprava - plotnost' atmosfery $\rho$ i dlina svobodnogo probega $\lambda_\infty$ v nevozmushennoi atmosfere

Pri zapisi uravneniya (2) bylo sdelano predpolozhenie, chto sila tyazhesti mg prenebrezhimo mala po sravneniyu s siloi soprotivleniya, chto vypolnyaetsya s bol'shoi tochnost'yu dlya meteornyh skorostei i nemalyh uglov vhoda k gorizontu (ne menee 5°, luchshe 10°). Kinematicheskoe uravnenie dlya opredeleniya vysoty z meteoroida ot vremeni t budet

$$\frac{dz}{dt}=-\upsilon \sin \Theta\,.$$ (3)

Pri otsutstvii sily tyazhesti i pod'emnoi sily (vtoroe predpolozhenie) traektoriya poleta meteoroida budet pryamoi liniei s zadannym i neizmennym uglom naklona $\Theta$ k gorizontu, ravnym uglu vhoda meteoroida v atmosferu.

Treh uravnenii (1),(2),(3) dostatochno dlya opredeleniya skorosti kak funkcii vysoty ili vremeni pri zadannyh m i ACD . Rezul'taty budut proshe i naglyadnee vyglyadet', esli vmesto vremeni t pereiti v uravnenii (2) k plotnosti $\rho$ kak k novoi nezavisimoi peremennoi. Integriruya poluchennoe takim obrazom uravnenie pri zadannom postoyannom proizvedenii ACD , poluchim

$$\upsilon=\upsilon_e\,\exp(-\bar{\rho}/2)\,,$$ (4)

gde $$\bar{\rho}={\rho}/{\rho_{m}}\,, \quad \rho_{m}={\beta \sin \Theta}/{h}\,, \quad \beta=m/(AC_{\upsilon})\,, \quad \rho=\rho_0\exp(-{z}/{h})\,.$$

Zdes' $\upsilon_e$ – skorost' vhoda meteoroida v atmosferu na vysote, gde plotnost' $\rho_e$ mozhno polozhit' ravnoi nulyu, $\beta$ – ballisticheskii koefficient. Nezavisimaya bezrazmernaya peremennaya v (4), ravnaya

$$\bar{\rho}=\frac{\rho hAC_{\upsilon}}{m\sin\Theta}=\frac{3\rho hC_{\upsilon}}{4\delta R \sin \Theta}$$

(dlya shara radiusa R s plotnost'yu $\delta$) i izvestnym obrazom zavisyashaya ot vysoty cherez $\rho$ (sm.(1)), predstavlyaet soboi meru vzaimodeistviya meteoroida s atmosferoi, ravnuyu otnosheniyu massy gaza, zametennoi meteoroidom $\rho AhC_D/\sin\Theta$ na ego puti do dostizheniya plotnosti $\rho$, umnozhennoi na koefficient soprotivleniya CD , k masse meteoroida. Pri dvizhenii v razrezhennoi atmosfere CD = 2 i v pokazatele eksponenty v (4) budet stoyat' tochno ukazannoe otnoshenie. Kogda zametennaya meteoroidom massa gaza, umnozhennaya na CD , sravnyaetsya s massoi meteoroida, togda $\bar{\rho}$= 1, to est' $\rho =\rho_m$ , i skorost' ego umen'shitsya v $\sqrt{e}$= 1,65 raza i stanet ravnoi $\upsilon_m = 0,61\upsilon_e$ . Smysl harakternoi plotnosti $\rho_m$ budet raskryt dalee.

Perehod k vysote, soglasno (1), daetsya vyrazheniem $$z=h\ln \frac{h\rho_0}{\beta \bar{\rho} \sin \Theta}\,.$$

$$z=h\ln\frac{h\rho_0}{\beta\bar{\rho}\sin\Theta}\,.$$ (5)

Zamedlenie meteoroida (ili tormozhenie) poluchaem iz (2) i (4)

$$-\dot{\upsilon}\equiv\frac{-d\upsilon}{dt}=\frac{\rho(\upsilon)^{2}}{2\beta}=\frac{\upsilon^{2}_{e}\sin \Theta}{2h}\bar{\rho}\exp(-\bar{\rho})\,,$$ (6)

otkuda vidno, chto s uvelicheniem $\bar{\rho}<1$ (umen'sheniem vysoty, sm.(1)) tormozhenie meteoroida snachala rastet, a zatem pri $\bar{\rho}>1$ padaet. Znachit, pri nekotorom $\bar{\rho}$ sushestvuet maksimal'noe tormozhenie. Ono budet, kak legko videt', dostigat'sya pri $\bar{\rho}=1$, to est' na vysote $z_m$ (sm. (5)) s plotnost'yu $\rho_m$:

$$z_{m}=h \ln \frac{h \rho_0}{\beta \sin \Theta}\,, \qquad \rho_m=\frac{\beta\sin\Theta}{h}\,.$$ (7)

Takim obrazom, maksimal'noe tormozhenie dostigaetsya togda, kogda zametaemaya meteoroidom po ego traektorii massa gaza sravnyaetsya s massoi samogo meteora. Samo maksimal'noe tormozhenie ili maksimal'naya peregruzka Gm dlya dvizheniya v atmosfere Zemli (v (6) nado podstavit' $\bar{\rho}$= 1) budet (g = 9,81 m/s2, h = 6,7 km)

$$|\dot{\upsilon}|\strut_{\max}=\frac{\upsilon^{2}_{e}\sin \Theta}{2he}\,,$$ (8)
$$|\dot{\upsilon}|\strut_{\max}=\frac{\upsilon^{2}_{e}\sin \Theta}{2he}\,,$$
$$G_{m}=\frac{|\dot{\upsilon}_m|}{g}=\frac{\upsilon^{2}_{e} \sin \Theta}{2ghe}=2,85 \upsilon^{2}_{e}\,, \quad [\upsilon_e]=\mbox{~km/s.}$$

Eto zamechatel'noe vyrazhenie dlya Gm govorit o tom, chto sama maksimal'naya peregruzka dlya dannoi atmosfery (planety), to est' pri zadannyh g i h, zavisit tol'ko ot skorosti i ugla vhoda i ne zavisit ot massy, formy i razmerov meteoroida! Ot etih parametrov budet zaviset', konechno, vysota zm (7), gde dostigaetsya maksimal'naya peregruzka.

Meteoroid pri tormozhenii ("rastyanutom udare") sovershaet rabotu nad atmosferoi, teryaya pri etom svoyu kineticheskuyu energiyu s vysotoi po eksponencial'nomu zakonu

$$K=\frac{m \upsilon^2}{2}=K_e\exp(-\bar{\rho})\,, \quad K_e=\frac{m\upsilon^2_e}{2}\,,$$ (9)

gde Ke – nachal'naya kineticheskaya energiya meteoroida pri podlete k planete. Teryaemaya kineticheskaya energiya idet na privedenie atmosfery v dvizhenie, ee nagrev, nagrev, plavlenie, isparenie, a takzhe razrushenie samogo meteoroida. V modeli ideal'nogo meteoroida my rassmatrivaem poteryu kineticheskoi energii tol'ko za schet tormozheniya.

Skorost' izmeneniya K na edinicu puti meteoroida l = - z / sin $\Theta$ (pogonnoe izmenenie energii) budet

$$\frac{dK}{dl}=\frac{\rho \sin \Theta}{h}\frac{dK}{d \rho}=-\frac{K_{e}\sin \Theta}{h} \bar{\rho} \exp (-\bar{\rho})\,.$$ (10)

Iz vyrazheniya (10) srazu sleduet, chto na traektorii sushestvuet tochka (vysota) maksimal'noi poteri kineticheskoi energii na edinicu dliny. V etoi tochke $\bar{\rho}$= 1, i ona sovpadaet, sledovatel'no, s tochkoi maksimal'nogo tormozheniya. Sama maksimal'naya pogonnaya poterya kineticheskoi energii

$$-\frac{dK}{dl}=\frac{K_{e}\sin \Theta}{he}\,.$$ (11)

Ostavshayasya kineticheskaya energiya v tochke maksimal'noi poteri kineticheskoi energii budet (sm. (9))

$$K_{m}=\frac{K_{e}}{e}=0.37K_{e}\,.$$

Takim obrazom, v tochke maksimal'nogo tormozheniya, sovpadayushei s tochkoi maksimal'noi poteri pogonnoi kineticheskoi energii, ostaetsya tol'ko 37% nachal'noi kineticheskoi energii meteoroida.

Konechno, eti vyvody ostayutsya spravedlivymi, tol'ko esli meteoroid dostigaet tochki $\bar{\rho}$= 1 do togo momenta, kogda on doletit do poverhnosti planety.

V dal'neishem ponadobitsya velichina skorostnogo napora $\rho\upsilon^2$, opredelyayushaya velichinu napryazhenii v tele, kotoraya, soglasno (6),

$$\rho\upsilon^{2}=-2\beta \dot{\upsilon}=\frac{2\beta \upsilon^{2}_{e}\sin \Theta}{2h}\bar{\rho} \exp(-\bar{\rho})= ep_{m}\upsilon^{2}_{m}\bar{\rho} \exp(-\bar{\rho})\,.$$ (12)

Maksimal'nyi skorostnoi napor dostigaetsya v toi zhe samoi tochke $\bar\rho$= 1 i raven

$$(\rho\upsilon^2)_max=\rho_m\upsilon^2_m=\frac{\beta\upsilon^2_e\sin\Theta}{he}\,.$$ (13)

Kolichestvennyi analiz vzaimodeistviya meteoroidov s atmosferoi

Privedem teper' nekotorye osnovnye sledstviya iz poluchennogo resheniya. Rassmotrim meteoroid v vide shara radiusa R = D/2 s plotnost'yu $\delta$, dvizhushegosya v atmosfere Zemli (h = 6,7 km, $\rho_0$ = 0,001750 g/sm3). Togda

$$\beta=\frac{m}{AC_D}=\frac{4\pi R^2\delta}{3\pi R^3C_D}=\frac{\delta D}{c}\,, \quad c=\frac{3}{2}C_D\approx\frac{3}{2}\,,$$

$$\rho_m=\frac{\beta\sin\Theta}{h}=\frac{\delta D\sin\Theta}{hc}\approx\frac{\delta D\sin\Theta}{10^6}$$

$$(h = 6,7\mbox{~km;} \quad h_c \sim 10^6 \mbox{~sm})\,,$$

$$[\delta]=\mbox{g/sm}^3, [D]=\mbox{sm}, \quad \bar{\rho}=\frac{\rho}{\rho_b}=\frac{10^{6} \rho}{\delta D \sin \Theta}\,.$$

Vysota maksimal'nogo tormozheniya i maksimal'noi poteri kineticheskoi energii zm (7) budet ($\bar{\rho}=1$, $\rho_0\exp(-z_m/h)=\rho_m$)

$$z_{m} =h \ln \frac{\rho_0}{\rho_m}=h \ln \frac{1750}{\delta D \sin \Theta}=$$
$$z_{m} =h \ln \frac{\rho_0}{\rho_m}=h \ln \frac{1750}{\delta D \sin \Theta}= 2,30h(\lg 1750-\lg \delta - \lg D \sin \Theta)\,.$$ (14)
$$z_{m} =h \ln \frac{\rho_0}{\rho_m}=h \ln \frac{1750}{\delta D \sin \Theta}=$$

Na ris. 2 privedena eta zavisimost'. Vysota, na kotoroi dlina svobodnogo probega ravna diametru shara D, umnozhennomu na $\sin\Theta$, oboznachena liniei $Kn=\lambda_{\infty}/(D\sin\Theta)=1.$ Eta liniya yavlyaetsya priblizhennoi granicei mezhdu svobodno-molekulyarnym i kontinual'nym rezhimami obtekaniya.

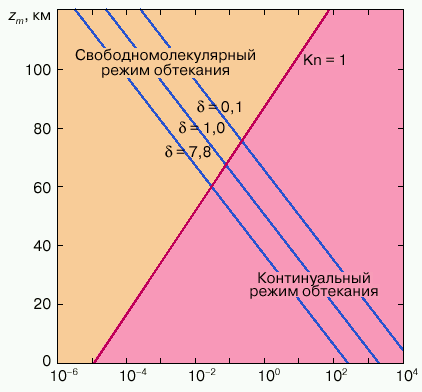Ris. 2. Vysota zm maksimal'nogo tormozheniya i maksimal'noi poteri pogonnoi kineticheskoi energii kak funkciya razmera i ugla vhoda meteoroida. Eto sootvetstvuet takzhe okrestnosti tochki maksimal'nogo teplovogo potoka. Liniya Kn = 1 yavlyaetsya priblizhennoi granicei mezhdu svobodnomolekulyarnym i kontinual'nym rezhimami obtekaniya. [$D\sin\Theta$] = sm, [$\delta$] = g/sm3.

Meteoroidy, razmery kotoryh men'she 0,1 mm (mikrometeoroidy), vletayushie v atmosferu Zemli s lyubymi skorostyami (do 72 km/s), budut tormozit'sya v oblasti svobodno-molekulyarnogo rezhima obtekaniya (sm. takzhe ris. 1). V silu malyh razmerov ($\bar{\rho}\rightarrow\infty$ ) oni tormozyatsya v verhnih sloyah atmosfery ran'she, chem nagrevayutsya do temperatury plavleniya, i teryayut vsyu svoyu kineticheskuyu energiyu (sm. (9)).

Krome togo, tela razmerom $D\gg$ 10 m mogut dostigat' poverhnosti Zemli, ne teryaya v atmosfere zametnoi doli svoei kineticheskoi energii ("proshivayut atmosferu"). Eto sleduet iz formuly (9), esli imet' v vidu, chto dlya poverhnosti Zemli $\bar{\rho} =\bar{\rho}_0=\rho_0\rho_m=\frac{1750}{(\delta\sin{\Theta})}\ll 1$, esli $D\gg$ 10 m ($\delta\geq$ 3 g/sm3). Pri etom oni progrevayutsya na tolshinu poryadka $\Delta(t) =0,1\sqrt t \simeq$ 0,2-0,3 mm (t \simeq 4-6 s), ne uspev poteryat' skol'ko-nibud' znachitel'noi doli svoei massy. Odnako zdes' ne sleduet upuskat' iz vidu bol'shoe aerodinamicheskoe davlenie, voznikayushee pri tormozhenii meteoroida i szhimayushee ego v napravlenii dvizheniya. Iz formuly (13), kotoruyu dlya shara mozhno perepisat' v vide

$$(\rho \upsilon^{2})\strut_{\max}=\frac{\beta \upsilon^{2}_{e}\sin \Theta }{he}\approx 0,01 D\upsilon^{2}_{e} \sin \Theta \mbox{~atm,}$$

$$\delta$$ = 2,72 g/sm3, [D] = sm, [$$\upsilon_e$$] = km/s,

mozhno ocenit' maksimal'nuyu nagruzku, esli ona dostigaetsya, deistvuyushuyu na lobovuyu poverhnost' meteoroida.

Naprimer, telo razmerom D = 100 sm pri vertikal'nom vhode ($\sin\Theta=1$) v atmosferu so skorost'yu 20 km/s budet ispytyvat' maksimal'noe davlenie, dostigaemoe v perednei kriticheskoi (lobovoi) tochke, ravnoe ($\rho\upsilon^2$)max = 400 atm. Predely prochnosti meteoroidov lezhat v shirokih predelah ot 0,01 do 500 atm (5),(6) v silu ih neodnorodnosti, nalichiya mikrotreshin i voobshe ryhlogo stroeniya nekotoryh iz nih. Poetomu oni drobyatsya chasto dazhe do dostizheniya maksimal'nogo davleniya. Bol'shie meteoroidy, kak pravilo, drobyatsya v atmosfere, obrazuya roi bystro tormozyashihsya fragmentov, kotorye, v svoyu ochered', popadaya v bolee plotnye sloi atmosfery, drobyatsya dalee, poka ne obrazuyutsya sil'no zatormozhennye i dalee ne drobyashiesya oskolki v silu povysheniya ih prochnosti s umen'sheniem razmerov, kotorye ili vypadayut na Zemlyu v vide meteoritov, ili, esli obrazuyutsya oskolki ves'ma malyh razmerov, rassypayutsya dalee pod deistviem termonapryazhenii ("teplovoi udar") do razmerov krupnoi pyli, kotoraya, okazavshis' v oblake goryachego gaza, pod deistviem konvektivnyh i radiacionnyh potokov plavitsya i isparyaetsya za desyatye doli sekundy (7). V etom sluchae v konce traektorii obrazuetsya "vzryv" meteoroida s maksimal'no bystroi peredachei ostavsheisya kineticheskoi energii okruzhayushei atmosfere planety s vypadeniem ostatkov (inogda neznachitel'nyh) meteornogo veshestva na poverhnost' planety. Etot scenarii "vzryva" mozhet byt' opisan matematicheski i daet horoshee soglasie s nablyudatel'nymi dannymi po drobleniyu i "vzryvu" krupnyh meteornyh tel, takih, kak Prishbram (Chehoslovakiya, 1959), Lost-Siti (SShA, 1970) i Innisfri (Kanada, 1977).

Literatura

[1]. Passey Q.R., Melosh H.J. Effects of Atmospheric Breakup on Crater Field Formation // ICARUS. 1980. Vol. 42, No 2. P. 211-233.
[2]. Dodd R.T. Meteority. M.: Mir, 1986.
[3]. Alvarez L.W., Alvarez W., Asaro F., Michel H.V. Extraterrestrial Cause for the Cretaceous–Tertiary Extinction // Science. 1980. Vol. 208. P. 1095-1108.
[4]. Bronshten V.A. Tungusskii meteorit: Istoriya issledovaniya. M.: Zvezdochet, 1999.
[5]. Bronshten V.A. Fizika meteornyh yavlenii. M.: Nauka, 1981. 416 s.
[6]. Verniani F. Structure and Fragmentation of Meteoroids // Space Sci. Rev. 1969. Vol. 10. P. 230-261.
[7]. Apshtein E.Z., Pilyugin N.N., Tirskii G.A. Unos massy i izmenenie formy trehmernogo tela pri dvizhenii v atmosfere Zemli // Kosmich. issled. 1979. T. 17, No 2. S. 246-255.
Publikacii s klyuchevymi slovami: Meteor - ionizacionnyi sled - meteorit - atmosfera Zemli
Publikacii so slovami: Meteor - ionizacionnyi sled - meteorit - atmosfera Zemli
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 2.2 [golosov: 46]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya