Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Avtomodel'noe techenie

Avtomodel'noe techenie - techenie zhidkosti (gaza), kotoroe ostaetsya mehanicheski podobnym samomu sebe pri izmenenii odnogo ili neskol'kih parametrov, opredelyayushih eto techenie. V mehanicheski podobnyh yavleniyah naryadu s proporcional'nost'yu geometricheskih razmerov soblyudaetsya proporcional'nost' mehanicheskih velichin - skorostei, davlenii, sil i t. d. (sm. Podobiya teoriya).

Avtomodel'noe techenie - chastnyi sluchai techeniya zhidkosti (gaza), kogda obshaya zadacha gidroaeromehaniki svoditsya k sisteme bezrazmernyh obyknovennyh differencial'nyh uravnenii i granichnyh uslovii, zavisyashih ot odnoi nadlezhashim obrazom vybrannoi bezrazmernoi nezavisimoi peremennoi. Blagodarya etomu zadacha rascheta techeniya uproshaetsya, i udaetsya poluchit' ee chislennoe, a v ryade sluchaev i analiticheskoe reshenie.

Tak, pri obtekanii beskonechnogo konusa sverhzvukovym ravnomernym potokom ideal'nogo gaza (ris. 1) nel'zya vydelit' harakternyi lineinyi razmer, poetomu pri rastyazhenii ili szhatii kartiny techeniya otnositel'no vershiny konusa O v proizvol'noe chislo raz kartina ne izmenyaetsya, t. e. ostaetsya podobnoi samoi sebe. Vse bezrazmernye harakteristiki techeniya - otnositel'nye skorosti, davleniya i t. d. zavisyat ot odnoi nezavisimoi geometricheskoi peremennoi - polyarnogo ugla $\theta$. 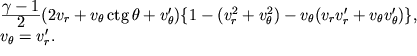Obtekanie konusa opisyvaetsya sistemoi iz dvuh uravnenii - s granichnymi usloviyami na poverhnosti konusa i na prisoedinennoi konicheskoi udarnoi volne: $ \begin{array}{ll} {\displaystyle \gamma -1\over\displaystyle 2}(2v_r+v_\theta\ctg\theta+v_\theta^\prime)\lbrace 1-(v_r^2 + v_\theta^2) - v_\theta(v_r v_r^\prime + v_\theta v_\theta^\prime)\rbrace, \\ v_\theta=v_r^\prime. \end{array} $ Zdes' $v_r, v_\theta$ - sostavlyayushie otnositel'noi skorosti v polyarnoi sisteme koordinat $r, \theta, \gamma=cp/cV$ - otnoshenie udel'nyh teploemkostei.

Avtomodel'noe techenie v laminarnom pogranichnom sloe sushestvuyut lish' pri nekotoryh special'nyh zakonah izmeneniya skorosti U vne pogranichnogo sloya, v chastnosti pri postoyannoi skorosti U=const (pogranichnyi sloi na prodol'no obtekaemoi beskonechnoi ploskoi plastine). T. k. v rassmatrivaemom techenii net kakoi-libo harakternoi dliny, to profili skorosti v v avtomodel'nom pogranichnom sloe v razlichnyh poperechnyh secheniyah x=const podobny drug drugu i v bezrazmernyh peremennyh predstavlyayutsya universal'noi funkciei ${\displaystyle v\over\displaystyle U}=\varphi(y/ \delta)$, gde u - rasstoyanie po normali k plastine, $\delta$ - tolshina pogranichnogo sloya. Bezrazmernaya funkciya toka $f(\zeta)$ v avtomodel'nom pogranichnom sloe udovletvoryaet obyknovennomu differencial'nomu uravneniyu
$f'''+\alpha ff'' + \beta(1-f'2)=0$
s granichnymi usloviyami $f=0, f' = 0$ pri $\zeta=0$ i $f' = 1$ pri $\zeta=\infty$. Zdes' $\alpha, \beta$ - nekotorye postoyannye, a $\zeta$ - bezrazmernaya avtomodel'naya peremennaya, proporcional'naya $u/ \delta$. Analogichnye avtomodel'nye techeniya vozmozhny i v pogranichnom sloe, voznikayushem iri svobodnoi (estestvennoi) konvekcii.

Avtomodel'noe techenie voznikaet i v osnovnom uchastke turbulentnoi svobodnoi strui (ris. 2), vytekayushei iz ploskogo ili kruglogo sopla v nepodvizhnuyu sredu, t. k. v shodstvennyh tochkah lyubyh dvuh poperechnyh sechenii bezrazmernye velichiny skorosti (temperatury, koncentracii) odinakovy. Dlya nestacionarnyh avtomodel'nyh techenii sostoyanie techeniya v nekotoryi moment vremeni t, harakterizuemoe raspredeleniem davlenii, skorostei, temperatur v prostranstve, mehanicheski podobno sostoyaniyu techeniya pri lyubom drugom znachenii t. Takie techeniya obrazuyutsya, naprimer, v sluchae sil'nogo vzryva, a takzhe pri rasprostranenii v goryuchei smesi fronta plameni ili detonacii. V sluchae sfericheskoi simmetrii vzryv (podzhiganie smesi) proishodit v tochke, v sluchae cilindricheskoi simmetrii - vdol' pryamoi, a v sluchae ploskih voln - vdol' ploskosti. Esli v moment t=0 mgnovenno vydelyaetsya konechnaya energiya E0, a nachal'naya plotnost' gazovoi sredy ravna $\rho_1$, to vvedenie bezrazmernoi avtomodel'noi peremennoi $\lambda=E_0t^2/ \rho_1r^{2+\nu}$ (gde r - rasstoyanie ot mesta vzryva, $\nu=3$ - dlya sfericheskih voln, $\nu=2$ - dlya cilindricheskih i \nu=1 - dlya ploskih) pozvolyaet svesti zadachu opredeleniya bezrazmernyh davlenii, skorostei, temperatur za vzryvnoi (udarnoi) volnoi k resheniyu sistemy obyknovennyh differencial'nyh uravnenii s avtomodel'nymi granichnymi usloviyami na udarnoi volne.

V shirokom smysle pod avtomodel'nost'yu techeniya inogda ponimayut nezavisimost' bezrazmernyh parametrov, harakterizuyushih techenie, ot kriteriev podobiya. Tak, koefficient lobovogo aerodinamicheskogo soprotivleniya SX (sm. Aerodinamicheskie koefficienty) mozhno schitat' avtomodel'nym po Maha chislu M ili Reinol'dsa chislu Re, esli v nekotorom diapazone ih izmeneniya SX ot nih ne zavisit. Avtomodel'nost' koefficienta SX po M i Re sushestvuet dlya bol'shinstva tel, obtekaemyh gazom, pri bol'shih M (M>8) ili dostatochno bol'shih Re (Re>107).


Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya 
Publikacii s klyuchevymi slovami: gidrodinamika - avtomodel'noe techenie - avtomodel'nost'
Publikacii so slovami: gidrodinamika - avtomodel'noe techenie - avtomodel'nost' 		Karta smyslovyh svyazei dlya termina AVTOMODEL'NOE TEChENIE
Sm. takzhe:

Obsudit' etu publikaciyu
Ocenka: 2.9 [golosov: 122]
 
O reitinge
Versiya dlya pechati Raspechatat'
Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya