Astronet > Avtokolebaniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Avtokolebaniya

$Ris. 1. Energeticheskaya shema ustanovleniya avtokolebanii: a - stacionarnyi rezhim ustoichiv; b - stacionarnyi rezhim neustoichiv./\n Ris. 2. Shemy generatorov Van der Polya: a - s kolebatel'nym konturom v cepi anoda; b - s kolebatel'nym konturom v cepi setki; v - harakteristika lampy./ /n Ris. 3. Oscillogrammy x(t), illyustriruyushie harakter ustanovleniya i formu avtokolebanii v sisteme (1) sootvetstvenno: a - kvazigarmonicheskie kolebaniya; b - sil'no nesinusoidal'nye // kolebaniya; v - relaksacionnye kolebaniya./ \\ Ris. 4. Fazovye portrety sistemy (1): a - kvazigarmonicheskie kolebaniya; b - sil'no nesinusoidal'nye kolebaniya; v - relaksacionnye kolebaniya./ Ris. 5. Fazovyi portret, otvechayushii zhestkomu vozbuzhdeniyu avtokolebanii: 1 - ustoichivyi predel'nyi cikl; 2 - neustoichivyi predel'nyi cikl; 3 - ustoichivoe sostoyanie ravnovesiya;/ Ris. 6. VAH tunnel'nogo dioda./ Ris. 7. Kol'cevaya truba, zapolnennaya zhidkost'yu, - konve$

Avtokolebaniya - nezatuhayushie kolebaniya v dissipativnoi nelineinoi sisteme, podderzhivaemye za schet energii vneshnego istochnika, parametry kotoryh (amplituda, chastota, spektr kolebanii) opredelyayutsya svoistvami samoi sistemy i ne zavisyat ot konechnogo izmeneniya nachal'nyh uslovii. Termin avtokolebaniya vveden A. A. Andronovym v 1928.

Avtokolebaniya principial'no otlichayutsya ot drugih kolebatel'nyh processov v dissipativnyh sistemah tem, chto dlya ih podderzhaniya ne trebuetsya kolebatel'nyh vozdeistvii izvne. Primery avtokolebanii: kolebaniya skripichnoi struny pri dvizhenii smychka, toka v radiotehnicheskom generatore, vozduha v organnoi trube, mayatnika v chasah. Voznikayut avtokolebaniya v rezul'tate razvitiya kolebatel'nyh neustoichivostei s ih posleduyushei stabilizaciei iz-za prekrasheniya postupleniya energii ot istochnika ili progressiruyushego vozrastaniya poter' (dissipacii). Rezhim stacionarnyh avtokolebanii opredelyaetsya iz usloviya energeticheskogo balansa - v srednem za period dissipativnye traty energii Q(I) (I - intensivnost' avtokolebanii) dolzhny tochno kompensirovat'sya postupleniem energii W(I) ot istochnika:

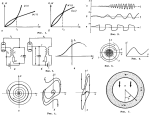
Q(I₀)=W(I₀). Esli v okrestnosti stacionarnogo rezhima I₀ energiya poter' Q (I) pri izmenenii I rastet bystree, chem pritok energii W(I), to etot rezhim avtokolebanii, s energeticheskoi tochki zreniya, ustoichiv (ris. 1, a); esli zhe bystree uvelichivaetsya W(I), to stacionarnyi rezhim neustoichiv (ris. 1, b). Dazhe v teh sluchayah, kogda mozhno vvesti funkcii Q i W, oni obychno zavisyat ne tol'ko ot intensivnostei avtokolebanii, no i ot ih faz, poetomu energeticheskii metod opredeleniya ustoichivosti avtokolebanii v obshem sluchae neprimenim. Sistemy, v kotoryh avtokolebaniya voznikayut "samoproizvol'no" - bez nachal'nogo tolchka, nazyvayutsya sistemami s myagkim rezhimom vozbuzhdeniya; esli dlya vozniknoveniya avtokolebanii neobhodim konechnyi nachal'nyi tolchok, to govoryat o zhestkom rezhime vozbuzhdeniya.

V prosteishih avtokolebatel'nyh sistemah mozhno vydelit' kolebatel'nuyu sistemu s zatuhaniem, usilitel' kolebanii, nelineinyi ogranichitel' i zveno obratnoi svyazi. Naprimer, v lampovom generatore (generatore Van der Polya, ris. 2, a, b) kolebatel'nyi kontur s poteryami, sostoyashii iz emkosti S, induktivnosti L i soprotivleniya R, predstavlyaet soboi dissipativnuyu kolebatel'nuyu sistemu, cep' "katod - setka" i induktivnost' L obrazuyut cep' obratnoi svyazi. Sluchaino voznikshie v kolebatel'nom konture malye sobstvennye kolebaniya cherez katushku L upravlyayut anodnym tokom lampy, kotoraya yavlyaetsya usilitelem. Pri polozhitel'noi obratnoi svyazi (t. e. pri opredelennom vzaimnom raspolozhenii katushek L i L₁) v kontur vnositsya opredelennaya energiya. Esli eta energiya bol'she energii poter' v konture, to amplituda malyh vnachale kolebanii v konture narastaet. Poskol'ku anodnyi tok lampy zavisit ot napryazheniya na setke nelineinym obrazom (ris. 2, v), to pri narastanii amplitudy kolebanii energiya, postupayushaya v kontur, umen'shaetsya i pri nekotoroi amplitude kolebanii stanovitsya ravnoi energii poter'. V rezul'tate ustanavlivaetsya rezhim stacionarnyh avtokolebanii, pri kotorom vneshnii istochnik (anodnaya batareya) kompensiruet vse poteri energii. T. o., avtokolebatel'nye sistemy dolzhny byt' principial'no nelineinymi - imenno nelineinost' ne pozvolyaet kolebaniyam bezgranichno narastat', upravlyaya postupleniem i tratami energii istochnika.

Chtoby opredelit' harakter avtokolebanii i zavisimost' ih amplitudy i formy ot parametrov sistemy, neobhodimo obratit'sya k analizu sootvetstvuyushei matematicheskoi modeli. Dlya prosteishego generatora (ris. 2, a) takoi model'yu mozhet sluzhit' uravnenie Van der Polya

$${\displaystyle d^2x\over\displaystyle t^2}-\mu(1-x^2){\displaystyle dx\over\displaystyle dt}+x=0$,$ (1)

kotoroe poluchaetsya pri prenebrezhenii setochnymi tokami lampy i approksimacii ee harakteristiki krivoi, predstavlennoi na ris. 2, v. Eto uravnenie zapisano v bezrazmernyh peremennyh, gde $x=\beta^{1/2}u; t=\omega_0t_1; \mu=\alpha\omega_0$ . Zdes' $\omega_0=\sqrt{LC}$ - sobstvennaya chastota kolebatel'nogo kontura, $\alpha=\sqrt{LC}(MS_0-RC)$ - parametr prevysheniya nad porogom generacii (pri $\alpha<0$ poterya v konture bol'she, chem vnosimaya energiya), $\beta=2MS_2(RC-MS_0)^{-1}$ harakterizuet amplitudu avtokolebanii, M - kozfficient vzaimnoi indukcii, S₀ i S₂ - parametry vol't-ampernoi harakteristiki usilitel'noi lampy. Tot fakt, chto avtokolebaniya v rassmatrivaemoi sisteme opisyvayutsya differencial'nym uravneniem 2-go poryadka (ego fazovoe prostranstvo - ploskost'), srazu nakladyvaet principial'nye ogranicheniya na vid avtokolebanii. V podobnyh sistemah vozmozhny tol'ko periodicheskie avtokolebaniya.

Geometricheskim obrazom ustanovivshihsya avtokolebanii v fazovom prostranstve sistemy sluzhit attraktor - traektoriya (ili mnozhestvo traektorii), raspolozhennaya v ogranichennoi oblasti fazovogo prostranstva i prityagivayushaya k sebe vse blizkie traektorii. Poskol'ku na fazovoi ploskosti traektorii peresekat'sya ne mogut, v sistemah 2-go poryadka mozhet sushestvovat' lish' prosteishii netrivial'nyi attraktor - zamknutaya traektoriya, k kotoroi stremyatsya vse blizhaishie traektorii. Takaya traektoriya nazyvaetsya predel'nym ciklom, kotoryi sluzhit obrazom periodicheskih avtokolebanii. Razmery predel'nogo cikla opredelyayut amplitudu avtokolebanii, vremya dvizheniya izobrazhayushei tochki po ciklu - period avtokolebanii, a forma predel'nogo cikla - formu kolebanii. Velichina $\mu$ harakterizuet nelineinost' sistemy: chem bol'she nelineinost', tem bol'she forma kolebanii otlichaetsya ot sinusoidal'noi (ris. 3). Pri malyh $\mu (\mu\ll 1)$ poteri v konture i vnosimaya v nego energiya ochen' maly - uravnenie (1) blizko k uravneniyu garmonicheskogo oscillyatora, a avtokolebaniya blizki k sinusoidal'nym s chastotoi $\omega_0=\sqrt{LC}$ .

V drugom predel'nom sluchae ( $\mu\gg 1$ ) poteri v konture i vnosimaya v nego energiya ochen' veliki po sravneniyu s energiei v nem zapasennoi, poetomu kolebaniya budut sil'no otlichat'sya ot sinusoidal'nyh, prevrashayas' v relaksacionnye. Analiz takih avtokolebanii udobno provodit', razdelyaya dvizheniya na uchastki bystryh i medlennyh dvizhenii (sm. Relaksacionnye kolebaniya}.

Pri izmenenii velichiny parametra $\mu$ ne proishodit nikakih kachestvennyh izmenenii v strukture razbieniya fazovoi ploskosti uravneniya (1) na traektorii - pri lyubom $\mu>0$ v sisteme imeetsya edinstvennoe sostoyanie ravnovesiya ( $h=0, dx/dt=0$ ), kotoroe neustoichivo, i edinstvennyi predel'nyi cikl, kotoryi ustoichiv, Kachestvennye perestroiki - bifurkacii proishodyat lish' pri smene znaka $\alpha$ . Rassmotrennaya kartina sootvetstvuet myagkomu rezhimu vozniknoveniya avtokolebanii, kotoromu sootvetstvuet fazovyi portret, izobrazhennyi na ris. 4, a. V sistemah s zhestkim rezhimom vozbuzhdeniya kolebaniya samoproizvol'no narastayut lish' s nekotoroi nachal'noi amplitudoi, t. e. kogda imeetsya tolchok s amplitudoi, bol'shei nekotorogo kriticheskogo znacheniya; pri etom na fazovom portrete (ris. 5) nachal'naya tochka dolzhna lezhat' vne zashtrihovannoi oblasti, t. e. izobrazhayushaya tochka dolzhna byt' vyvedena za predely oblasti prityazheniya ustoichivogo sostoyaniya ravnovesiya, granicei kotorogo sluzhit neustoichivyi predel'nyi cikl.

V sistemah, dazhe neznachitel'no bolee slozhnyh, chem generator na ris. 2, a, naprimer v sistemah s polutora stepenyami svobody, vozmozhny ne tol'ko periodicheskie i kvaziperiodicheskie avtokolebaniya (s neskol'kimi nesoizmerimymi chastotami), no i avtokolebaniya, nichem neotlichimye ot sluchainyh - t. n. stohasticheskie avtokolebaniya. Primerom takoi avtokolebatel'noi sistemy - generatora shuma, v kotorom haoticheskie kolebaniya (kolebaniya so sploshnym spektrom) sovershayutsya v dissipativnoi sisteme za schet energii regulyarnyh istochnikov, mozhet sluzhit' generator na ris. 2, b, esli v kontur posledovatel'no s induktivnost'yu dobavlen nelineinyi element s nevzaimno odnoznachnoi vol't-ampernoi harakteristikoi (ris. 6). Takim elementom yavlyaetsya, naprimer, tunnel'nyi diod. Matematicheskaya model' ili sootvetstvuyushaya takomu generatoru dinamicheskaya sistema mozhet byt' predstavlena v vide sistemy 3-go poryadka:

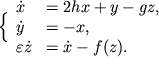$\Big\{ \begin{array}{ll} \dot x & = 2hx+y-gz, \\ \dot y & = -x, \\ \varepsilon \dot z & = \dot x-f(z). \end{array}$ (2)

Zdes' x, y, z - sootvetstvenno bezrazmernye toki v konture, napryazhenie na emkosti i napryazhenie na tunnel'nom diode, h - inkrement narastaniya kolebanii v konture v otsutstvie dioda, g harakterizuet stepen' vliyaniya dioda na processy v konture, $\varepsilon\ll 1$ - malyi parametr, proporcional'nyi emkosti tunnel'nogo dioda, f(z) - ego normirovannaya harakteristika. Fazovoe prostranstvo sistemy (2) trehmerno. Pri opredelennyh parametrah v etom fazovom prostranstve vse traektorii budut vhodit' v ogranichennuyu oblast', vnutri kotoroi net ni ustoichivyh sostoyanii ravnovesiya, ni ustoichivyh predel'nyh ciklov. Vnutri etoi oblasti soderzhitsya prityagivayushee mnozhestvo traektorii, kazhdaya iz kotoryh neustoichiva, - eto t. n. strannyi attraktor (attraktor Lorenca). Podobno tomu, kak predel'nyi cikl yavlyaetsya obrazom periodicheskih avtokolebanii, obrazom stohasticheskih avtokolebanii sluzhit strannyi attraktor.

Dlya avtokolebatel'nyh sistem s neskol'kimi stepenyami svobody harakterny takie yavleniya, kak sinhronizaciya i konkurenciya kolebanii. Razdelyayut vneshnyuyu sinhronizaciyu avtokolebanii, ili zahvatyvanie chastoty generatora, i vzaimnuyu sinhronizaciyu. Pri zahvatyvanii chastoty ustanavlivayutsya avtokolebanii s chastotoi i fazoi, sootvetstvuyushimi chastote i faze vneshnego periodicheskogo vozdeistviya, a pri vzaimnoi sinhronizacii - periodicheskie sfazirovannye kolebaniya v ansamble podsistem, kotorye v nezavisimom rezhime raboty harakterizuyutsya razlichnymi chastotami. Zahvatyvanie chastoty shiroko ispol'zuetsya dlya upravleniya i stabilizacii chastoty moshnyh malostabil'nyh generatorov s pomosh'yu vysokostabil'nyh malomoshnyh (naprimer, v lazerah). Polosa zahvatyvaniya - oblast' rasstroek mezhdu chastotami sobstvennyh kolebanii i vneshnim signalom, vnutri kotoroi ustanavlivaetsya rezhim sinhronizacii, - rasshiryaetsya pri uvelichenii amplitudy vneshnego vozdeistviya. Vne granicy zahvatyvaniya ustoichivyi rezhim generacii periodicheskih kolebanii smenyaetsya rezhimom bienii - rezhimom kvaziperiodicheskih kolebanii, - libo stohasticheskim rezhimom. Vzaimnaya sinhronizaciya podsistem ili razlichnyh elementarnyh kolebanii (mod) ispol'zuetsya pri rabote neskol'kih generatorov na obshuyu nagruzku, dlya polucheniya korotkih impul'sov v mnogomodovyh generatorah (naprimer, lazerah) i t. d.

Konkurenciya mod - podavlenie odnih mod drugimi v avtokolebatel'nyh sistemah - svyazana s tem, chto konkuriruyushie mody cherpayut energiyu na pokrytie dissipativnyh rashodov iz obshego istochnika. V rezul'tate odni mody sozdayut dopolnitel'noe nelineinoe zatuhanie dlya drugih. Blagodarya effektam konkurencii i vzaimnoi sinhronizacii kolebanii v avtokolebatel'nyh sistemah s bol'shim chislom stepenei svobody (ili dazhe beskonechnym chislom - v sluchae raspredelennyh sistem) vozmozhno ustanovlenie iz nachal'nogo shuma (narastayushih v rezul'tate razvitiya lineinyh neustoichivostei fluktuacii na razlichnyh chastotah) rezhima regulyarnyh periodicheskih avtokolebanii. Effekty konkurencii i sinhronizacii okazyvayutsya principial'nymi i dlya poyavleniya vysokoorganizovannyh struktur v nelineinyh neravnovesnyh sredah.

V raspredelennyh sistemah harakter avtokolebanii sushestvenno zavisit, pomimo vida nelineinosti, eshe i ot osobennostei dispersii sredy i granichnyh uslovii, v chastnosti nalichiya rezonatora. V nekotoryh sluchayah spektr vozbuzhdeniya mod i osobennosti ih nelineinogo vzaimodeistviya takovy, chto pri analize avtokolebanii v raspredelennoi sisteme s beskonechnym chislom stepenei svobody vozmozhno ogranichit'sya t. n. odnomodovym opisaniem. Dlya primera rassmotrim avtokolebaniya v kol'cevom rezonatore - raspolozhennoi v vertikal'noi ploskosti zamknutoi trube, zapolnennoi vyazkoi zhidkost'yu (ris. 7). Pri podogreve kol'ca snizu v sisteme ustanavlivaetsya rezhim konvekcii: bolee legkaya, nagretaya v osnovanii kol'ca chast' zhidkosti vsplyvaet, zastavlyaya ohlazhdennuyu zhidkost' opuskat'sya vniz. T. o., nachinaya s nekotoroi raznosti temperatur $T_v-T_n=\delta T_1$ ustanavlivaetsya rezhim stacionarnogo vrasheniya zhidkosti po ili protiv chasovoi strelki. Pri etim vsya zhidkost' vrashaetsya kak celoe - realizuetsya lish' odno naibolee krupnomasshtabnoe dvizhenie. Dal'neishee uvelichenie $\delta T$ $(\delta T_2>\delta T_1$ privodit k vozniknoveniyu avtokolebanii, proyavlyayushihsya v tom, chto zhidkoe kol'co vnutri truby vremya ot vremeni budet menyat' napravlenie svoego dvizheniya. Fizicheski eto mozhno poyasnit' tak: pust' v dannyi moment zhidkost' dvizhetsya po chasovoi strelke, pri dostatochno bol'shom $\delta T$ arhimedova sila velika i vodyanoe kol'co uskoryaetsya nastol'ko, chto ostyvshii vverhu zhidkii ob'em, proidya goryachee osnovanie i ne uspev nagret'sya, uzhe ne dostigaet verhnei chasti kol'ca i priostanavlivaetsya (arhimedova sila nedostatochna, chtoby preodolet' silu vyazkosti i gravitacii). Pri etom opuskayushayasya (pravaya) chast' zhidkosti teplee i, sledovatel'no, legche podnimayusheisya. V rezul'tate tormozheniya zhidkogo kol'ca zhidkost' v ego osnovanii nagrevaetsya i vsplyvaet, no uzhe v protivopolozhnom napravlenii - davlenie sprava men'she, chem sleva. T. o., zhidkoe kol'co menyaet napravlenie svoego vrasheniya i nachinaet zakruchivat'sya protiv chasovoi strelki. Zatem vse povtoryaetsya v obratnom poryadke. Takie vyzyvaemye teplovoi konvekciei avtokolebaniya mogut byt' kak periodicheskimi, tak i stohasticheskimi. Poskol'ku nikakie drugie masshtaby dvizheniya, krome osnovnogo, v avtokolebaniyah rassmatrivaemogo vida ne uchastvuyut, matematicheskaya model' dlya opisaniya etih avtokolebanii mozhet byt' poluchena iz ishodnyh uravnenii gidrodinamiki v predpolozhenii, chto zavisimost' polei skorosti i temperatury ot prostranstvennyh koordinat ne menyaetsya vo vremeni i proporcional'na $\sin \varphi$ , gde $\varphi$ - uglovaya koordinata elementarnogo ob'ema zhidkosti. V rezul'tate dlya bezrazmernyh skorosti x(t) dvizheniya zhidkogo kol'ca, temperatury u(t) zhidkosti v tochke N i temperatury z(t) v tochke M mozhno poluchit' sistemu uravnenii v obyknovennyh proizvodnyh:

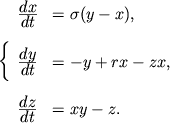
$\Bigg\{ \begin{array}{ll} {\displaystyle dx \over \displaystyle dt} & = \sigma(y-x), \\ \\ {\displaystyle dy \over \displaystyle dt} & = -y+rx-zx, \\ \\ {\displaystyle dz\over\displaystyle dt} & = xy-z. \end{array}$ (3)

gde $\sigma, r>0$ . Eto - izvestnaya sistema Lorenca (sm. Lorenca sistema), kotoraya yavlyaetsya odnoi iz osnovnyh modelei teorii stohasticheskih avtokolebanii. V zavisimosti ot parametrov $\sigma$ i r v fazovom prostranstve sistemy (3) mogut sushestvovat' kak ustoichivyi predel'nyi cikl, tak i strannyi attraktor.

V obshem sluchae avtokolebaniya v rezonatorah, kotorye opisyvayutsya uravnennyami v chastnyh proizvodnyh s sootvetstvuyushimi granichnymi usloviyami, nevozmozhno predstavit' s pomosh'yu konechnomernoi dinamicheskoi sistemy. Odnako, kak pravilo, blagodarya raznogo roda fizicheskim obstoyatel'stvam, naprimer nalichiyu dissipacii, progressiruyushei s rostom chastoty ili umen'sheniem prostranstvennogo masshtaba pul'sacii, takoe konechnomernoe opisanie okazyvaetsya spravedlivym.

V neravnovesnyh dissipativnyh sredah, pomimo avtokolebanii, o kotoryh rech' shla vyshe, vozmozhny eshe t. n. avtovolny i avtostruktury - ne svyazannye s granichnymi usloviyami prostranstvenno-vremennye obrazovaniya, parametry kotoryh opredelyayutsya lish' svoistvami nelineinoi neravnovesnoi sredy, naprimer uedinennye fronty goreniya i volny populyacii, impul'sy v nervnyh voloknah, cilindricheskie i spiral'nye volny v serdechnoi tkani i dr. Stohasticheskie avtokolebaniya v nelineinyh neravnovesnyh sredah - eto turbulentnost'.

"Fizicheskaya Enciklopediya"/Phys.Web.Ru
Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya

Publikacii s klyuchevymi slovami: avtokolebaniya Publikacii so slovami: avtokolebaniya
Sm. takzhe: Avtokolebaniya

Obsudit' etu publikaciyu

Versiya dlya pechati