Astronet > Zakon Ampera

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zakon Ampera

Zakon vzaimodeistviya postoyannyh tokov. Ustanovlen A.Amperom v 1820. Soglasno zakonu Ampera, sila $dF_{1\to2}$ , deistvuyushaya so storony odnogo elementarnogo "otrezka toka" $I_1d\vec l_1$ na drugoi $I_2d\vec l_2$ , ubyvaet obratno proporcional'no kvadratu rasstoyaniya mezhdu nimi $\vec r_{12}$ i v srede s magnitnoi pronicaemost'yu $\mu$ . mozhet byt' predstavlena v vide
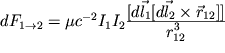$dF_{1\to 2}=\mu c^{-2}I_1 I_2{\displaystyle \lbrack d\vec l_1\lbrack d\vec l_2\times\vec r_{12}\rbrack\rbrack\over\displaystyle r_{12}^3}$ . (1)

Zdes' ispol'zovana Gaussa sistema edinic, s - skorost' sveta v vakuume. Vhodyashie v (1) elementarnye otrezki tokov yavlyayutsya chastyami zamknutyh konturov, poskol'ku postoyannye elektricheskie toki vsegda chisto solenoidal'nye (vihrevye). Poetomu zakon Ampera v forme (1) imeet lish' vspomogatel'nyi smysl, privodya k pravil'nym (podtverzhdaemym na opyte) znacheniyam sily tol'ko posle integrirovaniya (1) po zamknutym konturam $l_1$ i $l_2$ .

Naprimer, v obshem sluchae elementarnye sily mezhdu dvumya otrezkami tokov okazyvayutsya nevzaimnymi: $dF_{1\to 2}\neq dF_{2\to 1}$ odnako pri perehode k zamknutym konturam eta nevzaimnost' ustranyaetsya. Iz zakona Ampera sleduet, v chastnosti, chto dva pryamyh provoda s tokami $I_1$ i $I_2$ , tekushimi parallel'no ili antiparallel'no drug drugu na rasstoyanii d, sootvetstvenno prityagivayutsya ili ottalkivayutsya s siloi (na edinicu dliny), ravnoi $F_{1\to 2}=F_{2\to 1}=\pm 2\mu I_1 I_2/c^2d$ . A dva ploskih kontura s tokami $I_1$ i $I_2$ na rasstoyaniyah, sushestvenno prevyshayushih ih razmery, vzaimodeistvuyut mezhdu soboi kak dva magnitnyh dipolya i t. d. Iz zakonov Ampera i Bio-Savara vytekaet vyrazhenie dlya sily, deistvuyushei na tok v zadannom vneshnem magnitnom pole $\vec B=\mu\vec H$ ( $\vec H$ - napryazhennost' magnitnogo polya, $\vec B$ - magnitnaya indukciya), $d\vec F={\displaystyle 1\over\displaystyle c}I\lbrack d\vec l\times\vec B\rbrack$ . Otsyuda v sluchae proizvol'no raspredelennyh tokov s ob'emnoi plotnost'yu $\vec j=I\Delta\vec l/ \Delta V$ dlya sily na edinicu ob'ema $\vec f=\Delta\vec F/ \Delta V$ poluchaetsya
$\vec f={\displaystyle 1\over\displaystyle c}\lbrack\vec j\times\vec B\rbrack$ . (2)

Velichinu (2) nazyvayut siloi Ampera, a v sluchae konvektivnogo toka, obuslovlennogo dvizheniem zaryazhennyh chastic, $\vec j=\rho\vec v$ ( $\vec v$ - skorost', $\rho$ - ob'emnaya plotnost' zaryada), ona izvestna kak sila Lorenca.

Inogda zakonom Ampera nazyvaetsya integral'noe sootnoshenie $\oint\limits_C \vec Hd\vec l=4\pi\cdot\vec I/c$ , gde - polnyi tok, protekayushii cherez poverhnost', ogranichennuyu zamknutym konturom S. Eto sootnoshenie analogichno teoreme Gaussa v elektrostatike.

"Fizicheskaya Enciklopediya"/Phys.Web.Ru
Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya

Publikacii s klyuchevymi slovami: elektrichestvo - elektricheskii tok - zakon Ampera Publikacii so slovami: elektrichestvo - elektricheskii tok - zakon Ampera
Sm. takzhe: Gazovyi razryad Vakuumnyi proboi Anomal'noe soprotivlenie plazmy Barionii Teorema Ampera Amper

Obsudit' etu publikaciyu

Versiya dlya pechati