|
Teorema Ampera
Ustanavlivaet ekvivalentnost'
polei, sozdavaemyh magnitnym listkom i
postoyannym elektricheskim
tokom, tekushim
po konturu, sovmeshennomu s kraem etogo listka. Magnitnym
listkom nazyvaetsya uchastok poverhnosti S s ravnomerno
raspredelennymi na nem
elementarnymi magnitnymi dipolyami, napravlennymi
po normali ![]() k S
(ris. 1). Poverhnostnaya plotnost'
dipolei
k S
(ris. 1). Poverhnostnaya plotnost'
dipolei ![]() na listke svyazana s ekvivalentnym tokom I
sootnosheniem
na listke svyazana s ekvivalentnym tokom I
sootnosheniem ![]() (Gaussa
sistema edinic);
pri etom napravleniya
toka i normali
(Gaussa
sistema edinic);
pri etom napravleniya
toka i normali ![]() udovletvoryayut pravilu
pravogo vinta. V sluchae proizvol'nogo raspredeleniya vektora namagnichennosti
udovletvoryayut pravilu
pravogo vinta. V sluchae proizvol'nogo raspredeleniya vektora namagnichennosti
![]() (dipol'nogo momenta edinicy ob'ema) plotnost'
ekvivalentnogo toka
(dipol'nogo momenta edinicy ob'ema) plotnost'
ekvivalentnogo toka ![]() opredelyaetsya ravenstvom
opredelyaetsya ravenstvom ![]() , yavlyayushimsya
obobsheniem teoremy Ampera.
, yavlyayushimsya
obobsheniem teoremy Ampera.
V 1820 A. M. Amper eksperimental'no
pokazal, chto magnitnye svoistva vitka s tokom i postoyannogo
magnita na dostatochno bol'shih
rasstoyaniyah
odinakovy. V tom zhe godu on sformuliroval i dokazal teoremu Ampera s pomosh'yu predvoshitivshego
vyvod formuly Stoksa, rassuzhdeniya: pust' po zamknutomu
konturu ![]() , lezhashemu na poverhnosti S,
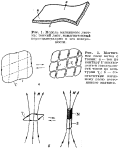
techet elektricheskii tok I. Poverhnost' S mozhno
razbit' na skol' ugodno bol'shoe chislo yacheek (ris.
2, a) i predstavit', chto po kazhdomu elementu poluchivsheisya setki tekut virtual'nye
toki, ravnye po velichine I i protivopolozhnye po napravleniyam,
tak chto summarnyi tok
v kazhdom vnutrennem elemente raven nulyu. V silu principa
superpozicii poluchennaya sistema virtual'nyh tokov ekvivalentna po svoemu
magnitnomu deistviyu
ishodnomu toku; s drugoi storony, kazhdyi elementarnyi vitok s tokom ekvivalenten
malen'komu magnitiku s dipol'nym momentom
, lezhashemu na poverhnosti S,
techet elektricheskii tok I. Poverhnost' S mozhno
razbit' na skol' ugodno bol'shoe chislo yacheek (ris.
2, a) i predstavit', chto po kazhdomu elementu poluchivsheisya setki tekut virtual'nye
toki, ravnye po velichine I i protivopolozhnye po napravleniyam,
tak chto summarnyi tok
v kazhdom vnutrennem elemente raven nulyu. V silu principa
superpozicii poluchennaya sistema virtual'nyh tokov ekvivalentna po svoemu
magnitnomu deistviyu
ishodnomu toku; s drugoi storony, kazhdyi elementarnyi vitok s tokom ekvivalenten
malen'komu magnitiku s dipol'nym momentom ![]() ,
gde
,
gde
![]() - ploshad' yacheiki (ris. 2, b).
- ploshad' yacheiki (ris. 2, b).
Teorema Ampera sygrala znachitel'nuyu rol' v stanovlenii predstavlenii o
edinoi prirode elektricheskih i magnitnyh yavlenii. Vmeste s principom
perestanovochnoi
dvoistvennosti teorema Ampera pozvolyaet ustanovit' sootvetstvie mezhdu
polyami v elektrostaticheskih i magnitostaticheskih sistemah (![]() ); s nekotorymi ogranicheniyami ego mozhno
perenesti i na peremennye polya.
); s nekotorymi ogranicheniyami ego mozhno
perenesti i na peremennye polya.
"Fizicheskaya Enciklopediya"/Phys.Web.Ru
Glossarii Astronet.ru
|
Publikacii s klyuchevymi slovami:
elektrichestvo - teorema Ampera - magnitnoe pole - elektricheskii tok
Publikacii so slovami: elektrichestvo - teorema Ampera - magnitnoe pole - elektricheskii tok |

|
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |