Astronet > Effekt anomal'nogo propuskaniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Effekt anomal'nogo propuskaniya

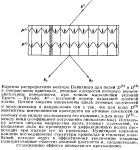
Rezkoe umen'shenie poglosheniya chasti potoka izlucheniya v tolstom ideal'nom kristalle pri lauevskom propuskanii. Effekt anomal'nogo propuskaniya vpervye nablyudalsya X. Bormanom v 1941 dlya rentgenovskih luchei luchei (effekt Bormana), pozdnee issledovan dlya neitronov, elektronov i gamma-luchei. Interpretaciya effekta predlozhena M. fon Laue (M. von Laue) v 1949.

Obychno intensivnost' rentgenovskih luchei pri rasprostranenii v kristalle eksponencial'no umen'shaetsya s glubinoi z proniknoveniya izlucheniya v kristall:
$G(z)=G_0e^{\displaystyle -\mu_0(\omega)z}$ , (1)

gde G₀ - intensivnost' pervichnogo polya; z - koordinata vdol' napravleniya rasprostraneniya; $\mu_0(\omega)={\displaystyle\omega\over\displaystyle c}|\gamma_i^0(\omega)|$ - lineinyi koefficient fotoelektricheskogo poglosheniya sredy; $\omega$ - chastota izlucheniya; $\gamma_i^0(\omega)$ - mnimaya chast' nulevoi fur'e-komponenty rentgenovskoi polyarizuemosti.

Zavisimost' (1) predpolagaet prostranstvennuyu odnorodnost' polya izlucheniya v kristalle ili neregulyarnoe stroenie (iskazhenie) kristalla i pravil'no opisyvaet oslablenie intensivnosti izlucheniya pri ego rasprostranenii v kristalle v proizvol'nom (ne difrakcionnom) napravlenii. Ona takzhe verna i pri kinematicheskoi difrakcii rentgenovskih luchei v tonkom (po sravneniyu s dlinoi pervichnoi ekstinkcii) kristalle. Esli tolshina kristalla $d\gg\mu_0^{-1}$ , to, soglasno (1), izluchenie polnost'yu pogloshaetsya v nem.

Pri dinamicheskoi difrakcii v usloviyah lauevskogo propuskaniya znachitel'naya chast' intensivnosti polya prohodit cherez tolstye ( $d\gg\mu_0^{-1}$ ) kristally, prakticheski ne oslablyayas'. Eto yavlenie i nazyvatesya effektom anomal'nogo propuskaniya. Pri dinamicheskoi difrakcii v kristalle ustanavlivaetsya prostranstvenno-neodnorodnaya struktura polya s masshtabom neodnorodnosti poryadka razmerov elementarnoi yacheiki kristalla. Dlya pravil'nogo opisaniya oslableniya intensivnosti takogo polya pokazatel' eksponenty v (1) dolzhen uchityvat' ne tol'ko velichinu fotoelektricheskogo poglosheniya, no i prostranstvennuyu strukturu polya.

Naibolee blagopriyatnym dlya nablyudeniya effekta anomal'nogo propuskaniya sluchaem yavlyaetsya simmetrichnoe lauevskoe propuskanie s-polyarizovannogo izlucheniya pri tochnom vypolnenii usloviya Bregga-Vul'fa. Pri etom otrazhayushie atomnye ploskosti perpendikulyarny vhodnoi poverhnosti kristallicheskoi plastiny, a vektor difrakcii $\vec g$ parallelen ei.

Rassmotrim effekt anomal'nogo propuskaniya dlya sluchaya, kogda imeetsya lish' 2 lucha - odin prohodyashii i odin difrakcionnyi (sm. ris. 1 k st. Dispersionnaya poverhnost'). Soglasno dinamicheskoi teorii difrakcii, pole v kristalle v etom sluchae dlya kazhdoi iz dvuh (s i r) polyarizacii (sm. Polyarizaciya sveta) sostoit iz chetyreh voln, poparno prinadlezhashih raznym listam dispersionnoi poverhnosti, opisyvayushei zavisimost' volnovogo vektora ot chastoty izlucheniya. Esli kristallograficheskie ploskosti centrosimmetrichnogo kristalla pri tochnom vypolnenii usloviya Vul'fa-Bregga perpendikulyarny poverhnosti kristalla, to summarnaya indukciya elektricheskogo polya elektromagnitnoi volny dlya kazhdogo lista dispersionnoi poverhnosti budet ravna
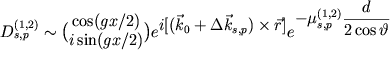$D_{s,p}^{(1,2)}\sim{\displaystyle\cos(gx/2)\choose\displaystyle i\sin(gx/2)}e^{\displaystyle i\lbrack(\vec k_0+\Delta\vec k_{s,p})\times\vec r\rbrack}e^{\displaystyle -\mu_{s,p}^{(1,2)}{\displaystyle d\over\displaystyle 2\cos{\vartheta}}}$ , (1)

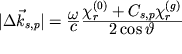gde $\vartheta$ - ugol Bregga, $\vec g$ - vektor obratnoi kristallicheskoi reshetki, $\vec k_0$ - volnovoi vektor pervichnoi volny, $|\Delta\vec k_{s,p}|={\displaystyle\omega\over\displaystyle c}{\displaystyle\chi_r^{(0)}+C_{s,p}\chi_r^{(g)}\over\displaystyle2\cos{\vartheta}}$ - dobavka k z-komponente vektora $\vec k_0$ za schet prelomleniya, $\chi_{r,i}^{(0,g)}$ - deistvitel'naya (r) i mnimaya (i) chasti fur'e-komponent rentgenovskoi polyarizuemosti, C_s=1, S_r = 2 cos $\vartheta$ ; lineinye koefficienty poglosheniya $\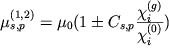mu_{s,p}^{(1,2)}=\mu_0(1\pm C_{s,p}{\displaystyle\chi_i^{(g)}\over\displaystyle\chi_i^{(0)}})$ , gde $\mu_0={\displaystyle1\over\displaystyle2}{\displaystyle\omega\over\displaystyle c}\chi_i^{(0)}$ . Chleny $\sim\chi_{r,i}^{(g)}$ v vyrazhenii dlya $\Delta\vec k_{s,p}$ i $\mu_{s,p}^{(1,2)}$ opisyvayut vliyanie interferencii na prelomlenie i pogloshenie izlucheniya pri difrakcii. 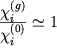Dlya s-polyarizacii iz-za slaboi zavisimosti $\chi_i^{(g)}$ ot $\sin {\displaystyle\vartheta\over\displaystyle\lambda}$ otnoshenie ${\displaystyle\chi_i^{(g)}\over\displaystyle\chi_i^{(0)}}\simeq1$ tak chto $\mu_s^{(1)}\simeq2\mu_0$ , a $\mu_s^{(2)}\ll\mu_0$ . Sledovatel'no, izluchenie s $D_s^{(1)}$ pogloshaetsya sil'nee, a s $D_s^{(2)}$ - slabee, chem v proizvol'nom napravlenii. Poetomu cherez kristall tolshinoi $d\gg\mu_0^{-1}$ mozhet prohodit' tol'ko izluchenie s $D_s^{(2)}$ . Proshedshee izluchenie imeet preimushestvennuyu s-polyarizaciyu, tak kak dlya r-polyarizacii $\chi_i^{(g)}\cos2\vartheta/chi_i^{(0)}\lt1$ i effekt anomal'nogo propuskaniya vyrazhen slabee. Effekt sushestvuet vo vsei uglovoi oblasti difrakcionnogo otrazheniya, odnako pri uvelichenii otstroiki $\Delta\vartheta$ ot tochnogo ugla Bregga $\vartheta$ on bystro oslablyaetsya.

Vektory Pointinga polei $D_{s,p}^{(1,2)}$ v sootvetstvii s (1) ravny:
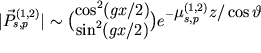$|\vec P_{s,p}^{(1,2)}|\sim{\displaystyle\cos^2(gx/2)\choose\displaystyle\sin^2(gx/2)}e^{-\displaystyle\mu_{s,p}^{(1,2)}z/ \cos\vartheta}$ (2)

i napravleny vdol' atomnyh ploskostei, a ih amplitudy v napravlenii, perpendikulyarnom atomnym ploskostyam, modulirovany s periodom, ravnym mezhploskostnomu rasstoyaniyu. Vsledstvie etogo $\vec P^{(1)}$ prinimaet maksimal'nye znacheniya na atomnyh ploskostyah, a $\vec P^{(2)}$ - mezhdu nimi (ris.). T.k. osnovnoi vklad v fotoelektricheskoe pogloshenie dayut vnutrennie K- i L-obolochki, elektronnaya plotnost' kotoryh sosredotochena vblizi atomnyh yader, pole $D^{(1)}$ rasprostranyaetsya v oblasti povyshennoi elektronnoi plotnosti, vzaimodeistvuet so sredoi i pogloshaetsya bolee intensivno, a pole $D^{(2)}$ rasprostranyaetsya v oblasti ponizhennoi elektronnoi plotnosti i vzaimodeistvuet so sredoi menee intensivno, chem v proizvol'nom, ne difrakcionnom napravlenii. Etim i obuslovleny anomal'no nizkoe pogloshenie v difrakcionnom napravlenii i poyavlenie rezkih maksimumov na rentgenogramme.

Teplovye kolebaniya atomov v kristalle effektivno uvelichivayut razmery atomov, tak chto $\mu_{s,p}^{(2)}$ vozrastaet. Naprimer, pri temperature $T\simeq$ 300 K
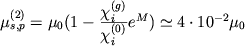$\mu_{s,p}^{(2)}=\mu_0(1-{\displaystyle\chi_i^{(g)}\over\displaystyle\chi_i^{(0)}}e^M)\simeq4\cdot10^{-2}\mu_0$ ,
gde $e^M$ - faktor Debaya-Vallera. Effekt anomal'nogo propuskaniya zavisit takzhe ot struktury kristalla. Lyubye otkloneniya ot ideal'nyh uslovii (atomnye ploskosti ne perpendikulyarny kristallograficheskim ploskostyam, nalichie otstroiki ot tochnogo ugla $\vartheta$ , defektov) umen'shayut effekt anomal'nogo propuskaniya. Pri mnogoluchevoi difrakcii mogut sushestvovat' oblasti, gde effekt anomal'nogo propuskaniya proyavlyaetsya eshe sil'nee.

Effekt anomal'nogo propuskaniya ispol'zuetsya dlya issledovaniya sovershenstva stroeniya kristallov (sm. Rentgenovskaya topografiya) i polucheniya slaborashodyashihsya puchkov monohromaticheskogo polyarizovannogo rentgenovskogo izlucheniya. Effekt anomal'nogo propuskaniya imeet mesto i dlya drugih izluchenii.

"Fizicheskaya Enciklopediya"/Phys.Web.Ru
Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya

Publikacii s klyuchevymi slovami: kristally - pogloshenie sveta - anomal'noe propuskanie Publikacii so slovami: kristally - pogloshenie sveta - anomal'noe propuskanie
Sm. takzhe: Neobychnye stolby sveta nad Latviei Klubnichnoe Solnce Solnechnyi stolb nad Ontario Piramidal'nye kristally l'da sozdayut galo nad Finlyandiei Galo i shestiugol'niki NGC 3314: pokrytie galaktik Raznocvetnye stolby sveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati