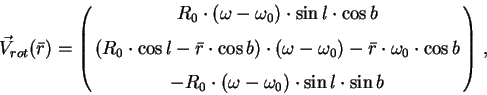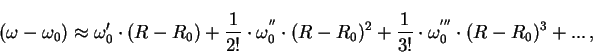Opredelenie krivoi vrasheniya i shkaly rasstoyanii v Galaktike<< 3. Sistemy koordinat | Oglavlenie | 5. Osnovnye formuly metoda >>
4. Kinematicheskaya model': dvizhenie Solnca, differencial'noe vrashenie
vyborki i "kosmicheskaya" dispersiya
Rassmotrim prosteishuyu kinematicheskuyu model' podsistemy,
vklyuchayushuyu tri komponenta: lokal'noe dvizhenie vyborki otnositel'no
Solnca, global'noe sistematicheskoe dvizhenie v forme
differencial'nogo vrasheniya i sluchainoe dvizhenie, opisyvaemoe
trehosnym ellipsoidal'nym raspredeleniem ostatochnyh skorostei
(Shvarcshil'dovskim). Rasseyanie ostatochnyh skorostei otnositel'no
centroida chasto nazyvayut "kosmicheskoi" dispersiei, podcherkivaya ih
otlichie ot vliyaniya oshibok nablyudenii (sm. dalee). Dlya prostoty
budem schitat' differencial'noe vrashenie barotropnym,
t.e. ne zavisyashim ot 
- koordinaty (hotya v principe legko
obobshit' model' na sluchai zavisimosti uglovoi skorosti ne tol'ko
ot 
, no i ot ). Takaya model' horosho predstavlyaet kinematiku
bol'shinstva ploskih galakticheskih podsistem. Model' mozhet byt'
uslozhnena putem vvedeniya nekrugovyh dvizhenii, vyzvannyh, naprimer,
vozmushayushim vliyaniem spiral'nyh rukavov [12]. Ono
osobenno sushestvenno dlya podsistem s maloi dispersiei skorostei,
t.e. molodyh ob'ektov - klassicheskih cefeid, rasseyannyh
skoplenii, OV-associacii i OV-zvezd. Tak, nablyudeniya gazovyh
diskov drugih spiral'nyh galaktikah pokazyvayut, chto velichina
vozmushenii skorosti mozhet dostigat' 20 - 30 km/s, chto zametno
bol'she "kosmicheskoi" dispersii skorostei gaza. Model' nekrugovyh
dvizhenii slozhna, ona zavisit ot sposoba opisaniya volny plotnosti,
i trebuet otdel'nogo obsuzhdeniya. Chto kasaetsya ellipsoida
skorostei, uslovimsya dlya prostoty schitat' ego formu i razmery ego
osei odinakovymi vo vsei izuchaemoi oblasti Galaktiki, hotya, kak
pokazyvayut vnegalakticheskie nablyudeniya, dispersii skorostei v
diskah spiral'nyh galaktik ubyvayut po mere udaleniya ot centra
galaktik i umen'sheniya poverhnostnoi plotnosti diska.
Na risunke
- sproektirovannoe na
ploskost' Galaktiki srednee (t.e. utochnennoe) rasstoyanie do
centroida 
, 
i 
- sootvetstvenno luchevaya skorost' i
tangencial'naya skorost' po galakticheskoi dolgote (vektor
tangencial'noi skorosti po galakticheskoi shirote, razumeetsya, ne
pokazan). Budem vyrazhat' sobstvennye dvizheniya v "/god, lineinye
(v tom chisle luchevye) skorosti v km/s, rasstoyaniya v kpk, a
uglovye skorosti v edinicah km/s/kpk. Dlya udobstva vvedem
koefficient
(km/s/kpk)("/god)
,
perevodyashii rasstoyaniya i sobstvennye dvizheniya v lineinye
skorosti, naprimer, v formule
, gde
- komponent tangencial'noi skorosti (po galakticheskoi
dolgote ili shirote).
Oboznachim mestnyi (okolosolnechnyi) centroid ob'ektov kak 
.
Pust' pri etom skorost' mestnoi vyborki otnositel'no Solnca ravna
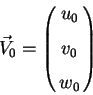
, gde komponenty skorosti zapisany v galakticheskoi pryamougol'noi sisteme koordinat (os'
kotoroi napravlena v centr Galaktiki,
os' 
- v storonu galakticheskogo vrasheniya, - k severnomu
polyusu Galaktiki). Rassmatrivaya treugol'nik i primeniv k
rasstoyaniyam teoremu kosinusov, legko vychislim rasstoyanie
centroida ot osi vrasheniya Galaktiki po geliocentricheskomu
rasstoyaniyu 
i ego galakticheskim koordinatam po formule
Proshe vsego rassmatrivat' raspredelenie skorostei ob'ektov v lokal'noi sisteme koordinat, privyazannoi k napravleniyu na ob'ekt i galakticheskim koordinatam
; v etoi sisteme koordinat
komponenty skorosti nam libo izvestny iz izmerenii (luchevaya
skorost'), libo mogut byt' legko vychisleny po rasstoyaniyu i
komponentam sobstvennogo dvizheniya (tangencial'nye skorosti po
galakticheskoi dolgote i shirote). Poskol'ku tangencial'nye
skorosti vychislyayutsya cherez prinyatoe rasstoyanie 
, vektor
nablyudaemoi skorosti v etoi sisteme koordinat mozhno zapisat' v
vide
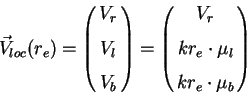
Legko pokazat', chto vklad differencial'nogo vrasheniya Galaktiki v nablyudaemuyu skorost' opisyvaetsya formulami Bottlingera [1], kotorye mogut byt' perepisany s ispol'zovaniem srednego rasstoyaniya
v lokal'noi sisteme
koordinat v vektornom vide
gde
i
- uglovye
skorosti issleduemogo centroida na rasstoyanii i na rasstoyanii
Solnca 
sootvetstvenno. Dlya resheniya obychno razlagayut raznost'
uglovyh skorostei v ryad Teilora
ogranichivayas', kak pravilo, vtorym ili tret'im poryadkom. Takoe razlozhenie daet horoshie rezul'taty dazhe dlya rasstoyanii 5 - 6 kpk ot Solnca. Nakonec, oboznachim cherez
istinnuyu
ostatochnuyu skorost' zvezdy otnositel'no centroida ,
obuslovlennuyu "kosmicheskoi" dispersiei.
<< 3. Sistemy koordinat | Oglavlenie | 5. Osnovnye formuly metoda >>
|
Publikacii s klyuchevymi slovami:
luchevaya skorost' - krivaya vrasheniya - Galaktika - metod maksimal'nogo pravdopodobiya
Publikacii so slovami: luchevaya skorost' - krivaya vrasheniya - Galaktika - metod maksimal'nogo pravdopodobiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
