Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu Geofizicheskie metody issledovaniya zemnoi kory

4.3.3. Pryamaya i obratnaya zadachi nad namagnichennym vertikal'nym beskonechno dlinnym stolbom (sterzhnem).

1. Pryamaya zadacha. Pust' na glubine $h$ zalegaet vershina beskonechno dlinnogo stolba (vertikal'nogo cilindra ili sterzhnya) secheniem $s$ (ris. 2.4). Ego mozhno predstavit' kak telo odnogo polyusa ($m$) s intensivnost'yu namagnicheniya ($J$), napravlennoi vdol' osi z, i "magnitnoi massoi" $m = Js$. Tak kak nizhnii polyus stolba raspolozhen ochen' daleko, to ego vliyaniem mozhno prenebrech' i schitat', chto vsya "massa" sosredotochena na vershine stolba.

Neobhodimo naiti napryazhennost' polya vdol' profilya x nad telom. Potencial ot verhnego polyusa stolba v tochke P budet raven potencialu tochechnoi massy (sm.2.4):

$U= \frac{m}{\mu r} = \frac{m}{\mu \sqrt{{x}^{2} +{h}^{2} } } .$(2.7)

Sostavlyayushie polya vyrazhayutsya proizvodnymi potenciala po sootvetstvuyushim osyam koordinat:

${Z}_{a} =- \frac{\partial U}{\partial h} = \frac{Jsh}{\mu ({x}^{2} +{h}^{2} {)}^{3/2} } , {H}_{a} =- \frac{\partial U}{\partial x} = \frac{Jsx}{\mu ({x}^{2} +{h}^{2} {)}^{3/2}} ,$(2.8)

${T}_{a} =\sqrt{Z_{a}^{2} +H_{a}^{2} } = \frac{Js}{\mu ({x}^{2} +{h}^{2} {)}^{5/2} } .$

Ispol'zuya poluchennye formuly, mozhno postroit' grafiki napryazhennosti polya (ris. 2.4). Legko videt', chto nad stolbom budut maksimumy $T_{ a}$ i $Z_{a}$, a znacheniya ih budut odnogo znaka, polozhitel'nye pri vertikal'noi $J_{ a}$. Gorizontal'naya sostavlyayushaya ($N$) sleva budet imet' maksimum, a sprava - minimum. Vdaleke ot stolba anomalii ischezayut. V plane nad takim stolbom izolinii $T_{ a}$ i $Z_{ a}$ budut imet' vid koncentricheskih okruzhnostei odnogo znaka.

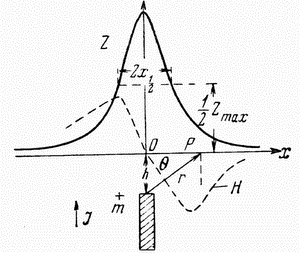Ris. 2.4. Magnitnoe pole vertikal'nogo beskonechno dlinnogo stolba

2. Obratnaya zadacha. Reshenie uravnenii (2.8) daet vozmozhnost' po harakternym tochkam na grafikah opredelit' glubinu zaleganiya verhnei kromki vertikal'nogo beskonechno dlinnogo stolba ( $h$). Tak centr stolba nahoditsya v tochke, gde $x = 0,$ a $Z_{ max} = T_{ max} = Js / mh^{ 2}.$

Dlya tochek, udalennyh na rasstoyaniya $x_{Z1/2}$ ot nachala koordinat, v kotoryh $Z$ ravno polovine maksimal'nogo

${Z}_{1/2} Jsh/2{h}^{2} \mu = Jsh/\mu ({x}^{2} + {h}^{2} {)}^{3/2}$

Reshiv eto uravnenie, poluchim $x_{Z1/2} = 0,7$ h. Analogichnym obrazom nahodyatsya svyazi i mezhdu drugimi harakternymi tochkami $x_{T1/2}$ , $x_{ HE}$ (ekstremumy na sostavlyayushei $N$), $x_{ ZH}$ (abscissy tochek peresecheniya $Z$ i $H$). V rezul'tate poluchayutsya sleduyushie formuly dlya rascheta $h$ po absolyutnym znacheniyam etih parametrov:

$h = 1,4|{X}_{HE} | = 1,3|{X}_{Z1/2} | = |{X}_{T1/2}| = |{X}_{ZH} |$(2.9)

Znaya $h$, mozhno ocenit' velichinu magnitnoi massy:
$m = Js = {Z}_{\max } \cdot \mu {h}^{2} = {T}_{\max } \mu {h}^{2}= 3,67{H}_{\max } \cdot \mu {h}^{2} .$

Tak kak $J \approx T_{ sr} \kappa$, gde $T_{ sr}$ - srednee znachenie polnogo vektora napryazhennosti polya v izuchaemom raione, a $\kappa$ - magnitnaya vospriimchivost' stolba, to

$\kappa s = m / T_{ sr}.$

Otsyuda, esli izvestno \kappa po izmereniyam na obrazcah, mozhno opredelit' ploshad' poperechnogo secheniya stolba ( $s$).

4.3.4. Pryamaya i obratnaya zadachi nad vertikal'no namagnichennym sharom.

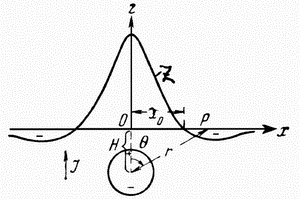1. Pryamaya zadacha. Pust' vertikal'no namagnichennyi shar s centrom na glubine $N$ zalegaet pod nachalom koordinat (ris. 2.5). Neobhodimo opredelit' napryazhennost' polya vdol' profilya $x$. Potencial shara mozhno predstavit' kak potencial dipolya, pomeshennogo v ego centre. Poetomu, soglasno (2.7), potencial shara s magnitnym momentom $M = JV$ (ili magnitnoi massoi $m = M$), raven:

$U = \frac{Mcos\theta }{\mu {r}^{2} } = \frac{MH}{\mu {r}^{3} } = \frac{JvH}{\mu ({x}^{2} + {H}^{2} {)}^{3/2} } .$(2.10)

Ris. 2.5. Magnitnoe pole shara

Otsyuda, vzyav proizvodnye, naidem elementy magnitnogo polya shara:
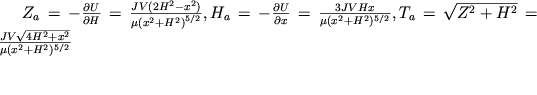${Z}_{a} = - \frac{\partial U}{\partial H} = \frac{JV(2{H}^{2} - {x}^{2} )}{\mu ({x}^{2} + {H}^{2} {)}^{5/2} } , {H}_{a} = - \frac{\partial U}{\partial x} = \frac {3JVHx}{\mu(x^2+H^2)^{5/2}}, T_a=\sqrt{Z^2+H^2}=\frac{JV\sqrt{4H^2+x^2}}{\mu(x^2+H^2)^{5/2}}$(2.11)

Analiz etih formul i postroennyh po nim grafikov pokazyvaet, chto nad centrom shara ( $h = 0$) budut $Z_{max} = T_{ max} = 2 JV / mH^{3},$ a $H = 0$. Pri $x \rightarrow \pm\infty$ anomalii ischezayut. Pri $x=\pm\sqrt{2} H$ $Z_{a} =0,$ pri $x\lt\sqrt{2}H $ $Z_{a} \gt 0$, a pri $x\gt\sqrt{2} H$ $Z_{a}\lt 0 .$

Takim obrazom, v plane nad sharom izolinii $Z_{ a}$ i $T_{ a}$ budut imet' vid koncentricheskih okruzhnostei. Pri etom izolinii $Z_{ a}$ budut dvuh znakov, a $T_{ a}$ - odnogo.

2. Obratnaya zadacha. Reshenie uravnenii (2.11) temi zhe priemami, chto i dlya stolba, daet vozmozhnost' po harakternym tochkam na grafikah naiti glubinu centra vertikal'no namagnichennogo shara:

Ha=1,8|xZ1/2|=1,8|xZH|=1,5|xT1/2|=0,7|xZ0|=0,5|xZmin|=(2.12)

gde $x_{Z1/2}$ i $x_{T1/2}$ - abscissy tochek poloviny $Z_{ a}, T_{ a}; x_{Z0}$ - tochki s $Z_{ a} = 0; x_{Zmin} $ tochki s $Z_{ a} = Z_{ min}.$

Znaya $H$, mozhno ocenit' magnitnuyu massu shara ( $m$):

$m = JV = {Z}_{\max } \mu {h}^{3/2} = {T}_{\max } \mu {h}^{3/2}$

Otsyuda, tak kak $J \approx \kappa T_{ sr},$ to $\kappa V \approx m / T_{ sr}.$ Esli izvestny $T_{ sr}$ i $ \kappa,$ mozhno opredelit' ob'em shara.

4.3.5. Pryamaya i obratnaya zadachi nad vertikal'no namagnichennym tonkim plastom beskonechnogo prostiraniya i glubiny.

Pust' na glubine $h$ parallel'no osi y raspolozhen beskonechno dlinnyi vertikal'nyi plast (s tolshinoi $l$, men'shei glubiny zaleganiya), namagnichennyi vertikal'no (ris. 2.6). Opredelim dlya prostoty lish' $Z_{ a}$ vdol' osi $x$.

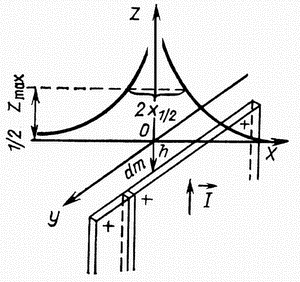Ris. 2.6. Magnitnoe pole tonkogo plasta beskonechnogo prostiraniya

Poskol'ku nizhnyaya chast' plasta raspolozhena gluboko, to vliyanie magnitnogo polyusa glubokih chastei plasta budet malo, i mozhno schitat', chto magnitnye massy sosredotocheny vdol' poverhnosti v vide lineinyh polyusov. Magnitnaya massa edinicy dliny plasta ravna $dm / dy = Jl.$

Razob'em plast na mnozhestvo tonkih "stolbov". Togda prityazhenie plasta budet skladyvat'sya iz prityazheniya vseh elementarnyh stolbov, a vertikal'naya sostavlyayushaya ego magnitnogo prityazheniya budet ravna integralu v predelah ot $-\infty$ do $+\infty$ (po osi $y$) vyrazheniya dlya prityazheniya elementarnogo stolba. Potencial elementarnogo tonkogo stolba raven

$dU = dm/\mu R = Jldy/\mu \sqrt{{x}^{2} + {y}^{2} + {h}^{2} }$

,

a vertikal'naya sostavlyayushaya $d{Z}_{a} = -\partial (dU)/\partial h = Jlhdy/\mu \sqrt{{x}^{2} + {y}^{2} + {h}^{2} } $ ,

otkuda $Z $ ravno

${Z}_{a} = {\int }_{-\infty }^{+\infty } \frac{Jlhdy}{\mu ({x}^{2} + {y}^{2} + {h}^{2} {)}^{3/2} } = \frac{2Jlh}{\mu ({x}^{2} + {h}^{2} )} .$(2.13)

Grafik $Z_{ a} $ budet imet' maksimum nad centrom plasta i asimptoticheski stremit'sya k nulyu pri udalenii ot plasta. V plane nad plastom budut vytyanutye anomalii $Z_{ a}$ odnogo znaka. Analiziruya formulu (2.13), mozhno naiti svyazi mezhdu glubinoi zaleganiya plasta ( $h$) i $x_{ 1/2}$, t.e. abscissoi grafika, gde $Z_{ a} = Z_{ max }/ 2; h = x_{ 1/2}.$

Magnitnaya massa edinicy dliny ravna $m = Jl = Z_{ max} \mu h /2$. Zameniv $J \approx \kappa T_{ sr}$, poluchim $l \kappa = m / T_{ cp}$. Znaya $T_{ cp}$ i $\kappa$, mozhno rasschitat' shirinu plasta.

Nazad| Vpered

Publikacii s klyuchevymi slovami: geofizika - Zemlya - zemnaya kora
Publikacii so slovami: geofizika - Zemlya - zemnaya kora
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [5]
Ocenka: 3.6 [golosov: 227]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya