Astronet > Geofizicheskie metody issledovaniya zemnoi kory. Chast' 1

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Geofizicheskie metody issledovaniya zemnoi kory

7.3. Principy resheniya pryamyh i obratnyh zadach elektrorazvedki

7.3.1. Obshie podhody k resheniyu pryamyh zadach elektrorazvedki.

V osnove teorii elektrorazvedki lezhat uravneniya Maksvella, yavlyayushiesya postulatami makroskopicheskoi elektrodinamiki. Oni vklyuchayut v sebya vse osnovnye zakony elektromagnetizma (zakony Oma, Ampera, Kirhgofa i dr.) i opisyvayut polya v raznyh sredah. Iz uravnenii Maksvella poluchaetsya differencial'noe uravnenie, nazvannoe telegrafnym. Reshaya ego, mozhno poluchit' elektricheskuyu ( $E$ ) komponentu polya v sredah vdali ot istochnika s elektromagnitnymi parametrami $\rho, \epsilon, \mu$ :

$\Delta E= \frac{\mu }{\rho } \frac{\partial E}{\partial t} +\epsilon\mu \frac{{\partial }^{2} E}{\partial {t}^{2} }$ , gde $\Delta E= \frac{{\partial }^{2} E}{\partial {x}^{2} } + \frac{{\partial }^{2} E}{\partial {y}^{2} } + \frac{{\partial }^{2} E}{\partial {z}^{2}}.$

(3.5)

Differencirovanie vedetsya po dekartovym koordinatam ( h, u, z) i vremeni ( $t$ ). Uravnenie dlya magnitnoi ( $N$ ) komponenty polya analogichno.

Esli geoelektricheskii razrez izvesten, to s pomosh'yu uravneniya (3.5) i fizicheskih uslovii zadachi, nazyvaemyh usloviyami sopryazheniya, reshayutsya pryamye zadachi elektrorazvedki, t.e. poluchayutsya analiticheskie ili chislennye znacheniya $E$ i $N$ , kotorye sootvetstvuyut zadannomu geoelektricheskomu razrezu. V teorii elektrorazvedki pryamye zadachi reshayutsya dlya raznyh fiziko-geologicheskih modelei (FGM) sred. Pod FGM ponimayutsya abstraktnye geoelektricheskie razrezy prostoi geometricheskoi formy, kotorymi approksimiruyutsya real'nye geologo-geofizicheskie razrezy. Slozhnost' resheniya pryamyh zadach zaklyuchaetsya v vybore modelei, blizkih k real'nym, no takih, chtoby dlya izbrannogo tipa pervichnogo polya udalos' poluchit' hotya by priblizhennoe reshenie dlya $E$ ili $N$ . Dlya etogo primenyaetsya matematicheskoe modelirovanie s ispol'zovaniem sovremennyh EVM. V nedalekom proshlom osnovnym sposobom resheniya pryamyh zadach dlya slozhnyh FGM i raznyh po strukture tipov polei yavlyalos' fizicheskoe modelirovanie na ob'emnyh ili ploskostnyh modelyah sred.

Naibolee prostymi modelyami sred yavlyayutsya:

odnorodnoe izotropnoe prostranstvo ili poluprostranstvo s odinakovymi elektromagnitnymi svoistvami (resheniya nad nimi nazyvayutsya sootvetstvenno pervichnym ili normal'nym polem istochnika);
anizotropnoe prostranstvo ili poluprostranstvo s elektromagnitnymi svoistvami, otlichayushimisya v napravlenii i vkrest sloistosti porod;
odnomernye neodnorodnye sredy, v kotoryh svoistva menyayutsya v odnom napravlenii. Takimi FGM mogut byt', naprimer, vertikal'nye kontakty dvuh sred, ryad vertikal'nyh plastov ili gorizontal'no sloistaya sreda s raznymi $\rho$ ;
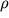dvuhmernye neodnorodnye sredy, v kotoryh elektromagnitnye svoistva menyayutsya v dvuh napravleniyah. Primerom mogut byt' naklonnye plasty ili cilindry, prostirayushiesya vdol' odnogo napravleniya i otlichayushiesya po 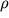$\rho$ ot vmeshayushih gornyh porod;
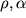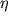trehmernye neodnorodnye sredy, v kotoryh svoistva menyayutsya po trem napravleniyam. Samoi prostoi iz podobnyh modelei yavlyaetsya shar s raznymi $\rho, \alpha$ ili $\eta$ v odnorodnom poluprostranstve.

V poryadke uvelicheniya slozhnosti struktury pervichnyh polei, a znachit vozrastaniya slozhnosti resheniya pryamyh zadach, ispol'zuemye dlya elektrorazvedki polya mozhno raspolozhit' v sleduyushei posledovatel'nosti: tochechnyh i dipol'nyh istochnikov postoyannogo toka, ploskih garmonicheskih elektromagnitnyh voln, sfericheskih voln dipol'nyh garmonicheskih ili impul'snyh istochnikov, cilindricheskih voln dlinnogo kabelya i t.p.

Sushestvuyut razlichnye podhody k resheniyu pryamyh zadach s pomosh'yu uravneniya (3.5). Lyuboe pravil'noe reshenie, udovletvoryayushee vsem fizicheskim trebovaniyam, edinstvenno i korrektno. Pod korrektnost'yu ponimaetsya takoe reshenie, v kotorom malym izmeneniyam ishodnyh dannyh sootvetstvuyut malye prirasheniya raschetnyh parametrov.

7.3.2. O normal'nyh polyah v elektrorazvedke.

Kak otmechalos' vyshe, pod normal'nym polem ponimaetsya elektromagnitnoe pole togo ili inogo istochnika nad odnorodnym izotropnym poluprostranstvom s neizmennymi elektromagnitnymi svoistvami.

Iz prosteishei pryamoi zadachi o pole tochechnogo istochnika postoyannogo toka na zemnoi poverhnosti (sm. 7.1.3) mozhno poluchit' normal'nye polya postoyannyh elektricheskih tokov dlya raznyh ustanovok ili raznyh kombinacii pitayushih ( AV) i priemnyh ( MN) elektrodov (sm. ris. 3.2).

V praktike elektrorazvedki chasto primenyayutsya chetyrehelektrodnye ustanovki AMNV (sm. ris. 3.2).

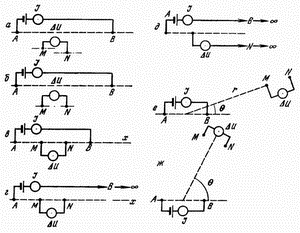Ris. 3.2. Plan raspolozheniya pitayushih (A i V) i priemnyh ( M i N) elektrodov v raznyh ustanovkah metoda soprotivlenii: a - chetyrehelektrodnoi, b - sredinnogo gradienta, v - simmetrichnoi chetyrehelektrodnoi, g - trehelektrodnoi, d - dvuhelektrodnoi, e - dipol'noi radial'noi, zh - dipol'noi azimutal'noi

K odnomu pitayushemu elektrodu (naprimer, A) podklyuchaetsya polozhitel'nyi polyus istochnika toka, k drugomu ( V) - otricatel'nyi. Raznost' potencialov na priemnyh elektrodah ( MN) ot elektroda A, opredelennaya po poluchennoi vyshe formule (3.1), ravna:

$\Delta U_{A} = \frac{J\rho }{2\pi} \left ( \frac{1}{AM} - \frac{1}{AN}\right ).$

Analogichnym obrazom mozhno poluchit' raznost' potencialov ot otricatel'nogo polyusa V, no velichinu toka sleduet prinyat' ravnoi ( $-J$ ).

Raznost' potencialov ot oboih elektrodov AV ravna superpozicii $\Delta U_{ A}$ i $\Delta U_{ B }$ :

$\Delta U = \frac{J\rho }{2\pi} \left ( \frac{1}{AM} - \frac{1}{AN} - \frac{1}{BM} + \frac{1}{BN}\right).$

(3.6)

Esli MN ustanovit' v centre AV tak, chtoby AM = BN, AN = VM, to poluchim formulu dlya rascheta $\rho$ simmetrichnoi chetyrehelektrodnoi ustanovki (sm. ris. 3.2):

$\rho = \pi \frac{AM\cdot AN}{MN} \cdot \frac{\Delta U}{J}.$

(3.7)

Potencial dvuhelektrodnoi ustanovki AM ( A i N udaleny v beskonechnost') mozhno poluchit' iz (3.6), prinyav $AN = VM = VN = \infty$ , t.e. $U = Jr / 2 \pi AM$ .

V metodah soprotivlenii primenyaetsya i ryad drugih ustanovok. Tak, naprimer, dlya glubinnyh issledovanii ispol'zuyutsya razlichnye dipol'nye ustanovki (ris. 3.2). Esli priemnyi dipol' ( MN) perpendikulyaren radiusu ( $r$ ) mezhdu ego centrom i centrom pitayushego dipolya ( AV), a ugol mezhdu radiusom i pitayushei liniei AV ( $\theta$ ) nahoditsya v predelah $70^\circ\lt\theta\lt 110^\circ$ , to takaya ustanovka nazyvaetsya azimutal'noi. Chastnym sluchaem azimutal'noi yavlyaetsya ekvatorial'naya ustanovka ( $\theta = 90^\circ$ ). Esli priemnyi dipol' (MN) napravlen vdol' $r$ , a $-30^\circ\lt\theta\lt +30^\circ$ , to takaya ustanovka nazyvaetsya radial'noi. Chastnym sluchaem radial'noi ustanovki yavlyaetsya osevaya ( $\theta = 0^\circ$ ).

Dlya kazhdoi ustanovki mozhno poluchit' formuly, po kotorym rasschityvaetsya koefficient ustanovki. Tak, dlya azimutal'noi ustanovki $K = 2 \pi r^3/ AB\cdot MN\cdot q$ , dlya radial'noi $K = \pi r^3/ AB\cdot MN\cdot p$ , gde $p$ i $q$ - koefficienty, malo otlichayushiesya ot edinicy i opredelyaemye po special'nym nomogrammam.

Takim obrazom, pri rabotah lyuboi ustanovkoi $\rho$ rasschityvaetsya po formule dlya normal'nogo polya

$\rho = K \frac{\Delta U}{J},$

(3.8)

gde $\Delta U$ - raznost' potencialov na MN, $J$ - tok v AV, a $K$ - koefficient ustanovki, zavisyashii lish' ot rasstoyanii mezhdu elektrodami.

Kak otmechalos' vyshe, po etim zhe formulam mozhno rasschitat' nekotoroe \rho nad real'nym, neizvestnym i prakticheski vsegda neodnorodnym poluprostranstvom. Togda ono nazyvaetsya kazhushimsya (KS ili $\rho_{ k}$ ).

Raschet normal'nyh polei dlya drugih istochnikov (garmonicheskih, impul'snyh) ochen' slozhen, no v lyubom sluchae prinyato poluchat' KS (sm. 7.1.3 - 7.1.5).

7.3.3. Elektricheskoe pole tochechnogo istochnika postoyannogo toka nad dvuhsloinoi sredoi.

Prosteishei, no ochen' vazhnoi dlya praktiki elektrorazvedki metodom soprotivlenii, odnomernoi pryamoi zadachei yavlyaetsya zadacha ob elektricheskom pole i kazhushemsya soprotivlenii na poverhnosti poluprostranstva, verhnee iz kotoryh vozduh, a nizhnee - dvuhsloinaya gorizontal'no sloistaya sreda s moshnost'yu verhnego sloya $h_{ 1}$ , nizhnego $h_{ 2} = \infty$ , UES sloev $\rho_{ 1}, \rho_{ 2}$ i $\rho_{ 3} = \infty$ (vozduh) (sm. ris. 3.3).

Postavlennaya zadacha mogla by byt' reshena s pomosh'yu uravneniya (3.2), kotoroe pri $f =0$ prevrashaetsya v uravnenie Laplasa $\Delta U = 0$ , gde $U$ - potencial v lyuboi tochke M s napryazhennost'yu elektricheskogo polya $E = h\partial U / \partial r$ .

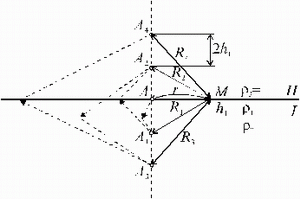Ris.. 3.3. Reshenie pryamoi zadachi o pole tochechnogo istochnika postoyannogo toka nad dvuhsloinoi sredoi metodom zerkal'nyh otrazhenii

Odnako ee mozhno bystro reshit' metodom zerkal'nyh otrazhenii. Soglasno pravilam metoda zerkal'nyh otrazhenii, urav-nenie Laplasa i fizicheskie trebovaniya, v tom chisle granichnye usloviya, vypolnyayutsya, esli potencial v odnomernoi srede, gde raspolozhen tochechnyi istochnik, prinyat' ravnym summe potencialov etogo istochnika ( $A$ ) i vseh ego mnogokratnyh otrazhenii ot granic razdela ( $A_{ 1}, A_{ 2}, A_{ 3}, \ldots$ ) s koefficientami otrazhenii, ravnymi na granice I $K_{ 12} = ( \rho_{ 2} - \rho_{ 1}) / ( \rho_{ 2} + \rho_{ 1})$ , a na granice II $K_{ 13} = ( \rho_{ 3} - \rho_{ 1}) / ( \rho_{ 3} + \rho_{ 1}) = 1$ (t.k. $\rho_{ 3} = \infty$ ).

Na ris. 3.3 pokazano, kak eti istochniki raspolozheny. Pri etom oboznacheno

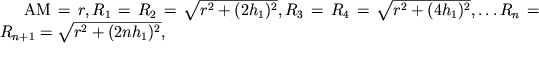$AM = r, R_{1} =R_{2} =\sqrt{r^{2} +(2h_{1})^{2} } , R_{3} =R_{4} =\sqrt{r^{2} +(4h_{1})^{2}} ,\ldots R_{n} = R_{n+1} = \sqrt{r^{2} + (2nh_{1})^{2} },$

gde $n = 1, 2, 3,\ldots , \infty$ .

Takim obrazom, iskomoe vyrazhenie dlya potenciala poluchaet vid:

$U = \frac{J{\rho }_{1} }{2\pi } \left [ \frac{1}{r} + 2\sum\limits_{n=1}^{\infty} \frac{K^{n}_{12}}{\sqrt{r^{2} + (2n{h}_{1} )^{2} } } \right ] .$

(3.9)

Vyrazhenie dlya KS (3.1) mozhno zapisat' v vide: $\rho_K = \frac{2\pi {r}^{2} }{J} \cdot \frac{\Delta U}{MN}$ , gde $\Delta U / MN = E$ - napryazhennost' elektricheskogo polya. No $E = h\partial U / \partial r$ , poetomu $\rho_K = \frac{2\pi {r}^{2} }{J} \cdot\left (\frac{\partial U}{\partial r} \right )$ . Podstaviv v etu formulu proizvodnuyu $\partial U / \partial r$ iz (3.9), poluchim

${\rho }_{K} = \frac{2\pi {r}^{2} }{J} \left ({ \frac{J{\rho }_{1} }{2\pi } }\right ) \cdot \left \{ { \frac{1}{{r}^{2} } + 2\sum\limits_{n=1}^{\infty }\frac{K^n_{12} r}{\left [r^2 + (2nh_1)^2\right]^{3/2}}}\right\}.$

Otkuda

${\rho }_{K} = {\rho }_{1} \left \{ {1 + 2\sum\limits_{n=1}^{\infty } \frac{K^n_{12} {r}^{3} }{[{r}^{2} + (2n{h}_{1})^{2}]^{3/2} } }\right \}.$

(3.10)

Analiziruya etu formulu, mozhno naiti asimptoticheskie vyrazheniya $\rho_{ k}$ , ravnye $\rho_{ 1}$ i $\rho_{ 2}$ . V samom dele, pri $r \rightarrow 0$ $\rho_{ k} = \rho_{ 1}$ , pri $r \rightarrow \infty$
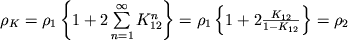$\rho_K =\rho_1\left\{ 1+2\sum\limits_{n=1}^{\infty} K_{12}^n\right\} = \rho_1\left\{ 1+2\frac{K_{12}}{1-K_{12}}\right\} =\rho_2$

(t.k. $K_{ 12} = ( \rho_{ 2} - \rho_{ 1}) / ( \rho_{ 2 }+ \rho_{1})$ , a $\sum K_{12}^{n}$ ravna $K_{ 12 }/ (1- K_{ 12})$ kak summa chlenov geometricheskoi progressii).

S pomosh'yu formuly (3.10), spravedlivoi dlya trehelektrodnoi i simmetrichnoi chetyrehelektrodnoi gradient-ustanovok, prinyato stroit' teoreticheskie dvuhsloinye krivye - grafiki zavisimosti $\lg ( \rho_{ K }/ \rho_{ 1}$ ) ot $\lg ( r / h_{ 1})$ . Oni nazyvayutsya dvuhsloinymi teoreticheskimi krivymi VEZ (vertikal'noe elektricheskoe zondirovanie) (sm. 8.2), ili dvuhsloinoi paletkoi VEZ (sm. ris. 3.4).

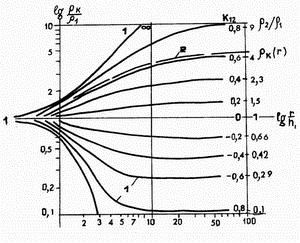Ris. 3.4. Dvuhsloinaya paletka VEZ: 1 i 2 - teoreticheskie i polevaya krivye

Bolee gromozdkoe reshenie poluchaetsya v zadache o pole tochechnogo istochnika nad mnogosloinoi gorizontal'no sloistoi sredoi, a eshe slozhnee reshenie dlya takoi zhe sredy, no pri vozbuzhdenii polya dipol'nymi garmonicheskimi ili impul'snymi istochnikami.

Odnomernye pryamye zadachi elektrorazvedki dlya mnogosloinyh gorizontal'no sloistyh sred dlya lyubyh pervichnyh polei vse-taki svodyatsya k analiticheskim formulam dlya rascheta KS. V rezul'tate prinyato stroit' krivye KS, analogichnye privedennym na ris. 3.4.

Dvuhmernye i trehmernye pryamye zadachi elektrorazvedki svodyatsya k analiticheskim formulam lish' dlya tel prostoi formy (shar, plast, cilindr) v odnorodnoi srede. V bolee obshih sluchayah poluchayutsya lish' priblizhennye chislennye resheniya, poluchaemye s pomosh'yu EVM.

Nazad| Vpered

Publikacii s klyuchevymi slovami: geofizika - Zemlya - zemnaya kora Publikacii so slovami: geofizika - Zemlya - zemnaya kora
Sm. takzhe: Voshod Zemli: video Udarnyi krater Manikuagan: vid iz kosmosa Zemlya i Luna: vid s drugoi storony Snezhnaya burya 1938 goda v Verhnem Michigane Polet nad nochnoi Zemlei – II Apollon-17: serp Zemli Samyi bol'shoi kamen' v nashei Solnechnoi sisteme Vse publikacii na tu zhe temu >>

Mneniya chitatelei [5]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce