Astronet > Geofizicheskie metody issledovaniya zemnoi kory. Chast' 1

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Geofizicheskie metody issledovaniya zemnoi kory

Glava 1. Gravirazvedka

1. Osnovy teorii gravitacionnogo polya Zemli i gravirazvedki

1.1. Sila tyazhesti, ee potencial i proizvodnye potenciala

1.2. Normal'noe znachenie sily tyazhesti, redukcii, anomalii sily tyazhesti i plotnost' gornyh porod

1.3. Principy resheniya pryamyh i obratnyh zadach gravirazvedki

2. Apparatura, metodika i obrabotka dannyh gravirazvedki

2.1. Principy izmerenii sily tyazhesti i apparatura dlya gravirazvedki

2.2. Metodika gravimetricheskih s'emok

2.3. Metodiki drugih vidov gravirazvedki

3. Interpretaciya i zadachi, reshaemye gravirazvedkoi

3.1. Kachestvennaya i kolichestvennaya interpretaciya dannyh gravirazvedki

3.2. Geologicheskie zadachi, reshaemye gravirazvedkoi

Gravimetricheskaya ili gravitacionnaya razvedka (sokrashenno gravirazvedka) - eto geofizicheskii metod issledovaniya zemnoi kory i razvedki poleznyh iskopaemyh, osnovannyi na izuchenii raspredeleniya anomalii polya sily tyazhesti Zemli vblizi zemnoi poverhnosti, akvatoriyah, v vozduhe. Pole sily tyazhesti obuslovleno v osnovnom N'yutonovskim prityazheniem Zemlei vseh tel, obladayushih massoi. Tak kak Zemlya sfericheski neodnorodna, da eshe vrashaetsya, to pole sily tyazhesti na zemnoi poverhnosti nepostoyanno. Izmeneniya eti maly i trebuyut vysoko-chuvstvitel'nyh priborov dlya ih izucheniya. Osnovnymi izmeryaemymi parametrami gravitacionnogo polya yavlyayutsya uskorenie sily tyazhesti i gradienty (izmeneniya uskoreniya po raznym napravleniyam). Velichiny parametrov polya sily tyazhesti zavisyat, s odnoi storony, ot prichin, obuslovlennyh prityazheniem i vrasheniem Zemli (normal'noe pole), a s drugoi storony - ot neravnomernosti izmeneniya plotnosti porod, slagayushih zemnuyu koru (anomal'noe pole). Eti dve osnovnye prichiny izmeneniya sily tyazhesti na Zemle posluzhili osnovoi dvuh napravlenii gravimetrii: geodezicheskoi gravimetrii i gravitacionnoi razvedki.

Ot drugih metodov razvedochnoi geofiziki gravirazvedka otlichaetsya sravnitel'no bol'shoi proizvoditel'nost'yu polevyh nablyudenii i vozmozhnost'yu izuchat' gorizontal'nuyu (lateral'nuyu) neodnorodnost' Zemli. Gravirazvedka primenyaetsya dlya resheniya samyh razlichnyh geologicheskih zadach s glubinnost'yu issledovanii ot neskol'kih metrov (naprimer, pri razvedke okrestnostei gornyh vyrabotok) do 200 kilometrov (naprimer, pri izuchenii mantii).

1. Osnovy teorii gravitacionnogo polya Zemli i gravirazvedki

1.1. Sila tyazhesti, ee potencial i proizvodnye potenciala

1.1.1. Sila tyazhesti.

Siloi tyazhesti ( $F$ ) nazyvayut ravnodeistvuyushuyu dvuh sil - sily n'yutonovskogo prityazheniya vsei massoi Zemli ( $F_n$ ) i centrobezhnoi sily, voznikayushei vsledstvie sutochnogo vrasheniya Zemli ( $R$ ). Otnesennye k edinice massy, eti sily harakterizuyutsya uskoreniyami sily tyazhesti g=F/m, n'yutonovskogo prityazheniya f=F_n/m i centrobezhnym P=P/m. Uskorenie sily tyazhesti ravno geometricheskoi summe uskoreniya prityazheniya i centrobezhnogo uskoreniya (ris. 1.1). Obychno v gravimetrii, kogda govoryat "sila tyazhesti", podrazumevayut imenno uskorenie sily tyazhesti.

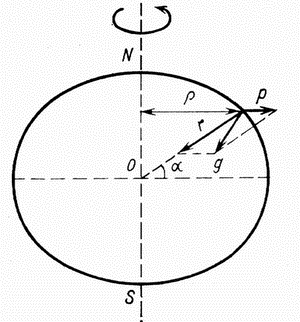Ris. 1.1 Uskorenie sily tyazhesti i ego sostavlyayushie

Edinicei uskoreniya v sisteme SI yavlyaetsya m/s². V gravimetrii tradicionno ispol'zuyut bolee melkuyu edinicu - Gal, ravnyi 1 sm/s². V srednem na Zemle g=981 Gal. V praktike gravirazvedki primenyaetsya velichina v 1000 raz men'shaya, poluchivshaya nazvanie milligal (mGal).

Sila prityazheniya kakoi-libo massy ( $m$ ) vsei massoi Zemli ( $M$ ) opredelyaetsya zakonom vsemirnogo tyagoteniya N'yutona:
$F_n\approx G\frac{mM}{r^2}$ (1.1)

gde $r$ - rasstoyanie mezhdu centrami mass $m$ i $M$ , t.e. radius Zemli; $g$ - gravitacionnaya postoyannaya, ravnaya G=6,67*10^-11 m³/kg*s². Sila prityazheniya edinichnoi massy (m=1) ravna $f\approx GM/r^2$ i napravlena k centru Zemli.

Centrobezhnaya sila ( $P$ ) napravlena po radiusu, perpendikulyarnomu osi vrasheniya ( $R$ ), i opredelyaetsya formuloi
$$P=mR\omega^{2}$,$ (1.2)

gde $\omega$ - uglovaya skorost' vrasheniya Zemli.

Velichina $P$ izmenyaetsya ot nulya na polyuse (R=0) do maksimuma na ekvatore. Otnoshenie $P/F\leq 1/288$ , poetomu sila tyazhesti pochti celikom opredelyaetsya siloi prityazheniya, a uskorenie sily tyazhesti prakticheski ravno uskoreniyu prityazheniya $g\approx f \approx GM/ r^2$ .

Zemlya v pervom priblizhenii yavlyaetsya ellipsoidom vrasheniya, prichem ekvatorial'nyi radius $a\approx 6378 \hbox{km}$ , a polyarnyi $c\approx 6357 \hbox{km}$ , a-c=21 km. Raznaya velichina radiusa Zemli na polyuse i ekvatore naryadu s izmeneniem centrobezhnoi sily privodit k uvelicheniyu $g$ na polyuse (g_p=983 Gal) po sravneniyu s $g$ na ekvatore (g_e= 978 Gal). Po izvestnym $g$ i $r$ byli opredeleny massa Zemli M=5,98*10²⁴ kg i ee srednyaya plotnost' $\sigma_z=5,51\cdot 10^3 \hbox{kg/m}^3 (5,51 \hbox{g/sm}^3)$ .

1.1.2. Potencial sily tyazhesti.

Potencial sily tyazhesti ( $W$ ) byl vveden v teoriyu gravimetrii dlya oblegcheniya resheniya teoreticheskih zadach. V tochke A, raspolozhennoi na rasstoyanii r_A ot centra Zemli, vyrazhenie dlya potenciala prinimaetsya ravnym: W_A=GM/r_A, a v lyuboi tochke B, raspolozhennoi na prodolzhenii radiusa $r$ , $W_B=GM/(r_A+\Delta r)$ . Poetomu raznost' potencialov budet ravna:

$$\Delta W=W_B-W_A=GM/\left[ \frac{-\Delta r}{r_A (r_A +r_B)}\right]$.$

V predele pri malom $\Delta r$ imeem:

$\Delta W =-GM\Delta r/r^2 =-g\Delta r,$

otsyuda g=-dW/dr, t.e. sila tyazhesti est' proizvodnaya potenciala sily tyazhesti po napravleniyu k centru Zemli.

S drugoi storony, rabota, kotoraya mozhet byt' proizvedena pri dvizhenii prityagivaemoi tochki po otrezku $\Delta r$ , ravna $\Delta A=g\Delta r$ . Poetomu $\Delta W = -\Delta A$ , ili rabota sily tyazhesti po peremesheniyu edinichnoi massy na otrezke $\Delta r$ ravna raznosti znachenii potenciala na koncah etogo otrezka.

Pri peremeshenii tochki v napravlenii, perpendikulyarnom sile tyazhesti, dW=0. Eto oznachaet, chto W=const. Poetomu gravitacionnoe pole mozhno predstavit' v vide nabora beskonechnogo chisla poverhnostei, na kotoryh potencial ostaetsya postoyannym, a uskorenie sily tyazhesti napravleno perpendikulyarno etoi poverhnosti. Takie poverhnosti nazyvayut ekvipotencial'nymi ili urovennymi. V chastnosti, poverhnost' zhidkosti na Zemle, naprimer, morya, sovpadaet s urovennoi poverhnost'yu. U Zemli est' odna unikal'naya urovennaya poverhnost', kotoraya sovpadaet s nevozmushennoi volneniyami poverhnost'yu okeanov. Ona nazyvaetsya geoidom.

Takim obrazom, geoid - eto uslovnaya urovennaya poverhnost', kotoraya sovpadaet so srednim urovnem okeanov i otkrytyh morei, prohodit pod sushei i po opredeleniyu vezde gorizontal'na, a uskorenie sily tyazhesti k nei perpendikulyarno.

1.1.3. Proizvodnye potenciala sily tyazhesti.

Proizvodnye potenciala sily tyazhesti po trem koordinatnym osyam $g_x=\partial W/\partial x$ , $g_y=\partial W/\partial y$ , $g_z=\partial W/\partial z$ odnoznachno opredelyayut ego polnyi vektor.

V chastnosti, esli os' z napravit' k centru Zemli, to $\frac{\partial W}{\partial x} = \frac{\partial W}{\partial y} =0$ , a $$g= \frac{\partial W}{\partial z}$.$

V gravimetrii krome pervyh proizvodnyh izuchayutsya vtorye proizvodnye potenciala ili ih raznosti:

$\frac{\partial^2 W}{\partial x\partial y}, \frac{{\partial }^{2} W}{\partial x\partial z}, \frac{{\partial }^{2} W}{\partial y\partial z}, \frac{{\partial }^{2} W}{\partial x^2}, \frac{{\partial }^{2} W}{\partial y^2}, \frac{{\partial }^{2} W}{\partial z^2}, \frac{{\partial }^{2} W}{\partial x^2}-\frac{{\partial }^{2} W}{\partial y^2}.$ (1.3)

Fizicheskii smysl etih vyrazhenii legko poluchit', esli imet' v vidu, chto $g=\partial W/\partial z$ . Tak, naprimer, vtoraya proizvodnaya $\frac{{\partial }^{2} W}{\partial x\partial z} = \frac{\partial g}{\partial x}$ ukazyvaet na skorost' izmeneniya sily tyazhesti po osi h, t.e. yavlyaetsya gorizontal'nym gradientom sily tyazhesti.

Analogichnyi smysl imeyut vtorye proizvodnye $\partial^2 W/\partial x \partial z$ i $\partial^2 W/\partial z^2$ .

Vtorye proizvodnye ${\partial }^{2} W/\partial x\partial y$ , ${\partial }^{2} W/\partial {x}^{2} -{\partial }^{2} W/\partial {y}^{2}$ harakterizuyut formu urovennoi poverhnosti (geoida), izuchaemuyu v geodezicheskoi gravimetrii. Prakticheskoi edinicei izmereniya gradienta sily tyazhesti prinimaetsya 1 etvesh (E)=10^-9/c², chto sootvetstvuet izmeneniyu sily tyazhesti v 0,1 mGal na 1 km.

Nazad | Vpered

Publikacii s klyuchevymi slovami: geofizika - Zemlya - zemnaya kora Publikacii so slovami: geofizika - Zemlya - zemnaya kora
Sm. takzhe: Protivosumerechnye luchi i festival' planet Voshod Zemli: video Udarnyi krater Manikuagan: vid iz kosmosa Zemlya i Luna: vid s drugoi storony Snezhnaya burya 1938 goda v Verhnem Michigane Polet nad nochnoi Zemlei – II Apollon-17: serp Zemli Vse publikacii na tu zhe temu >>

Mneniya chitatelei [5]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce