9.1.2. Fiziko-matematicheskaya kolichestvennaya interpretaciya elektromagnitnyh zondirovanii.
Fiziko-matematicheskaya kolichestvennaya interpretaciya elektromagnitnyh zondirovanii, kotoraya, v osnovnom, svoditsya k resheniyu obratnoi zadachi, horosho razrabotana dlya odnomernyh (gorizontal'no sloistyh) modelei sred (sm. 7.3). V rezul'tate poluchayutsya parametry: posloinye moshnosti (![]() ), soprotivleniya (
), soprotivleniya (![]() ), polyarizuemosti (
), polyarizuemosti (![]() ) ili obobshennye dlya tolshi (moshnosti
) ili obobshennye dlya tolshi (moshnosti ![]() , prodol'nye provodimosti
, prodol'nye provodimosti ![]() , prodol'nye udel'nye soprotivleniya
, prodol'nye udel'nye soprotivleniya ![]() , poperechnye soprotivleniya
, poperechnye soprotivleniya ![]() , poperechnye udel'nye soprotivleniya
, poperechnye udel'nye soprotivleniya ![]() ). Sushestvuyut razlichnye metody resheniya obratnyh zadach: grafoanaliticheskie, paletochnye i s pomosh'yu EVM (mashinnye) (sm. 7.3.1).
). Sushestvuyut razlichnye metody resheniya obratnyh zadach: grafoanaliticheskie, paletochnye i s pomosh'yu EVM (mashinnye) (sm. 7.3.1).
1. Grafoanaliticheskie metody. V rezul'tate analiza reshenii pryamyh zadach EMZ polucheny analiticheskie sposoby rascheta obobshennyh parametrov razreza po asimptoticheskim ili ekstremal'nym znacheniyam KS na krivyh EMZ, poluchivshie nazvanie grafoanaliticheskih.
Naibol'shee primenenie nahodit metod ![]() . Esli krivaya EMZ poluchena nad razrezom s ochen' vysokim soprotivleniem v osnovanii (naprimer, kristallicheskim fundamentom), to provedya pod uglom 45
. Esli krivaya EMZ poluchena nad razrezom s ochen' vysokim soprotivleniem v osnovanii (naprimer, kristallicheskim fundamentom), to provedya pod uglom 45![]() (dlya VEZ-DZ) ili 63
(dlya VEZ-DZ) ili 63![]() (dlya MTZ, ChZ, ZS) k pravoi vetvi krivoi asimptotu, mozhno opredelit' summarnuyu prodol'nuyu provodimost' (
(dlya MTZ, ChZ, ZS) k pravoi vetvi krivoi asimptotu, mozhno opredelit' summarnuyu prodol'nuyu provodimost' (![]() ) tolshi nad nim. Velichina
) tolshi nad nim. Velichina ![]() ravnyaetsya
ravnyaetsya ![]() (dlya VEZ, DZ),
(dlya VEZ, DZ), ![]() (dlya MTZ),
(dlya MTZ), ![]() (dlya ChZ v dal'nei volnovoi zone),
(dlya ChZ v dal'nei volnovoi zone), ![]() (dlya ZSD),
(dlya ZSD), ![]() (dlya ZSB), gde
(dlya ZSB), gde ![]() - abscissy, a
- abscissy, a ![]() - ordinaty lyuboi tochki asimptoty.
- ordinaty lyuboi tochki asimptoty.
Na ris. 3.10 po pravoi asimptote ![]() = 330 (1/Om). Znaya
= 330 (1/Om). Znaya ![]() i opredeliv srednee prodol'noe soprotivlenie etoi tolshi (
i opredeliv srednee prodol'noe soprotivlenie etoi tolshi (![]() ), naprimer, po parametricheskim EMZ u skvazhin, putem analiza svyazei pered asimptotoi s
), naprimer, po parametricheskim EMZ u skvazhin, putem analiza svyazei pered asimptotoi s ![]() (obychno
(obychno ![]() ) i drugimi sposobami, mozhno rasschitat' glubinu zaleganiya vysokoomnogo gorizonta
) i drugimi sposobami, mozhno rasschitat' glubinu zaleganiya vysokoomnogo gorizonta ![]() . V rassmatrivaemom nami primere (sm. ris. 3.10)
. V rassmatrivaemom nami primere (sm. ris. 3.10) ![]() m.
m.
Sushestvuet ryad i drugih grafoanaliticheskih priemov opredeleniya razlichnyh parametrov razreza.
2. Paletochnye metody. 1). Paletochnye metody
interpretacii, primenyayushiesya v elektrorazvedke dolgie gody, osnovany
na ispol'zovanii al'bomov trehsloinyh krivyh (paletok), razlichnyh
dlya raznyh EMZ i rasschitannye dlya gorizontal'no-sloistyh modelei
sred (sm. 9.1.1). Sushnost' paletochnyh sposobov svoditsya k posledovatel'nomu
sovmesheniyu vystroennoi na kal'ke polevoi krivoi s teoreticheskimi
krivymi. Oni dolzhny byt' postroeny v odinakovom logarifmicheskom masshtabe.
Dobivshis' nailuchshego sovmesheniya po indeksam sovpavshei teoreticheskoi
krivoi i paletki, opredelyayut moshnost' (![]() ) i udel'noe elektricheskoe soprotivlenie (
) i udel'noe elektricheskoe soprotivlenie (![]() ) pervogo (verhnego) sloya, otnositel'nye znacheniya moshnosti
) pervogo (verhnego) sloya, otnositel'nye znacheniya moshnosti ![]() i soprotivleniya
i soprotivleniya ![]() vtorogo sloya, a takzhe
vtorogo sloya, a takzhe ![]() interpretiruemoi krivoi. Otsyuda mozhno naiti priblizhennye znacheniya izuchaemogo razreza:
interpretiruemoi krivoi. Otsyuda mozhno naiti priblizhennye znacheniya izuchaemogo razreza: ![]() .
.
Pri interpretacii mnogosloinyh krivyh oni s pomosh'yu
tak nazyvaemyh vspomogatel'nyh paletok posledovatel'no (sverhu-vniz)
razbivayutsya na trehsloinye. Dlya etogo snachala dva verhnih sloya zamenyayutsya
odnim ekvivalentnym, t.e. takim fiktivnym sloem moshnost'yu ![]() i soprotivleniem
i soprotivleniem ![]() , chtoby elektromagnitnoe
pole na zemnoi poverhnosti ostavalos' tem zhe. Dalee tri verhnih sloya
zamenyayutsya novym ekvivalentnym s moshnost'yu
, chtoby elektromagnitnoe
pole na zemnoi poverhnosti ostavalos' tem zhe. Dalee tri verhnih sloya
zamenyayutsya novym ekvivalentnym s moshnost'yu ![]() i soprotivleniem
i soprotivleniem ![]() i tak dalee. Ispol'zuya
trehsloinye teoreticheskie paletki, poluchennye ekvivalentnye trehsloinye
krivye interpretiruyut kak obychnye trehsloinye.
i tak dalee. Ispol'zuya
trehsloinye teoreticheskie paletki, poluchennye ekvivalentnye trehsloinye
krivye interpretiruyut kak obychnye trehsloinye.
V rezul'tate interpretacii krivyh EMZ s pomosh'yu
al'bomov paletok poluchaetsya nabor fiziko-geometricheskih parametrov:
![]() , po kotorym mozhno opredelit'
priblizhennye posloinye znacheniya moshnostei i soprotivlenii:
, po kotorym mozhno opredelit'
priblizhennye posloinye znacheniya moshnostei i soprotivlenii:
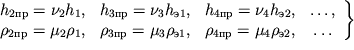 | (3.12) |
Oni blizki k istinnym lish' pri ![]() 3 - 5, a s umen'sheniem
3 - 5, a s umen'sheniem
![]() pogreshnosti v opredelenii posloinyh parametrov razreza
rezko vozrastayut. Eto ob'yasnyaetsya nekorrektnost'yu resheniya obratnoi
zadachi elektrorazvedki, kak i lyuboi zadachi matematicheskoi fiziki,
i sushestvovaniem principa ekvivalentnosti, t.e. neodnoznachnosti interpretacii
i vozmozhnosti sootvetstviya odnoi krivoi EMZ mnozhestvu geoelektricheskih
razrezov. Puti ego ucheta rassmotreny nizhe (sm. 9.1.3).
pogreshnosti v opredelenii posloinyh parametrov razreza
rezko vozrastayut. Eto ob'yasnyaetsya nekorrektnost'yu resheniya obratnoi
zadachi elektrorazvedki, kak i lyuboi zadachi matematicheskoi fiziki,
i sushestvovaniem principa ekvivalentnosti, t.e. neodnoznachnosti interpretacii
i vozmozhnosti sootvetstviya odnoi krivoi EMZ mnozhestvu geoelektricheskih
razrezov. Puti ego ucheta rassmotreny nizhe (sm. 9.1.3).
2). Uskorennaya interpretaciya krivyh EMZ mozhet provodit'sya
s pomosh'yu nomogramm-paletok, podgotovlennyh V.K.Hmelevskim dlya kazhdogo
metoda EMZ. Oni pozvolyayut zamenyat' pri interpretacii gromozdkie al'bomy
paletok (v raznyh metodah EMZ nabory tipichnyh trehsloinyh krivyh
menyayutsya ot neskol'kih desyatkov do sot listov) odnoi-dvumya nomogrammami-paletkami.
Na ris. 3.11 privedena nomogramma-paletka dlya interpretacii krivyh
vertikal'nyh (VEZ) i dipol'nyh, azimutal'nyh i ekvatorial'nyh (DAZ
i DEZ) zondirovanii na postoyannom toke. Ona sostoit iz vspomogatel'noi
(sleva) i dvuhsloinoi (sprava) paletok, ob'edinennyh obshim nachalom
koordinat (krest paletki). Na vspomogatel'noi paletke privedeny shkaly
sleduyushih parametrov i sootvetstvuyushie im krivye: a) sleva shkala
![]() , ocifrovyvayushaya krivye ravnyh znachenii
, ocifrovyvayushaya krivye ravnyh znachenii ![]() dlya vseh tipov trehsloinyh krivyh
dlya vseh tipov trehsloinyh krivyh ![]() ; b) sverhu privedeny shkaly
; b) sverhu privedeny shkaly ![]() , a vnizu -
, a vnizu - ![]() dlya sploshnyh i punktirnyh vertikal'nyh ili pochti vertikal'nyh krivyh
dlya sploshnyh i punktirnyh vertikal'nyh ili pochti vertikal'nyh krivyh ![]() na nomogramme. Na dvuhsloinoi paletke
po osi
na nomogramme. Na dvuhsloinoi paletke
po osi ![]() otlozheny raznosy, normirovannye moshnost'yu verhnego
sloya (
otlozheny raznosy, normirovannye moshnost'yu verhnego
sloya (![]() ), a po osi
), a po osi ![]() - znacheniya
- znacheniya ![]() , shkala kotoryh raspolozhena krainei sprava. Zdes' zhe prochercheny teoreticheskie (paletochnye) dvuhsloinye krivye, sploshnye (dlya VEZ, DAZ, DEZ).
, shkala kotoryh raspolozhena krainei sprava. Zdes' zhe prochercheny teoreticheskie (paletochnye) dvuhsloinye krivye, sploshnye (dlya VEZ, DAZ, DEZ).
 |
| Ris. 3.11. Nomogramma-paletka dlya interpretacii krivyh VEZ, DEZ, DAZ |
Posledovatel'nost' interpretacii s pomosh'yu nomogrammy-paletki rassmotrim na primere pyatisloinoi krivoi VEZ-DEZ tipa KQH, privedennoi na ris. 3.10. Dlya etogo ona dolzhna byt' vycherchena na kal'ke s logarifmicheskim masshtabom po osyam koordinat s takim zhe modulem M, kak i nomogramma-paletka.
- Polevaya mnogosloinaya krivaya razbivaetsya na dvuhsloinye, i samaya levaya iz nih (I - II) nakladyvaetsya na dvuhsloinuyu paletku. Soblyudaya parallel'nost' osei koordinat paletki i blanka s polevoi krivoi, dobivayutsya nailuchshego ee sovmesheniya s odnoi iz teoreticheskih. Na blank perenositsya krest paletki - t. O1, koordinaty kotoroi na osyah ordinat i absciss ravny
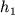 i
i 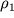 . Po pravoi shkale paletki ocenivaetsya
. Po pravoi shkale paletki ocenivaetsya 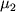 .
. - S dvuhsloinoi paletkoi sovmeshaetsya vtoraya vetv' polevoi krivoi (II - III), i na blank vnov' perenositsya krest paletki O2 s koordinatami
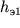 i
i 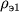 . Polozhenie tochki O1 na nomogramme daet utochnennye parametry
. Polozhenie tochki O1 na nomogramme daet utochnennye parametry 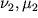 , znacheniya kotoryh snimayutsya s sootvetstvuyushih shkal (v rassmatrivaemom primere dlya pervoi krivoi tipa
, znacheniya kotoryh snimayutsya s sootvetstvuyushih shkal (v rassmatrivaemom primere dlya pervoi krivoi tipa 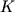 eti parametry opredelyayutsya po shkalam:
eti parametry opredelyayutsya po shkalam: 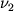 po
po 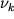 i
i 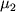 po levoi shkale.
po levoi shkale. - S dvuhsloinoi krivoi sovmeshaetsya tret'ya vetv' (III - IV), i na blank perenositsya krest paletki O3 (
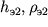 ), a po polozheniyu tochki O2 na nomogramme opredelyayutsya
), a po polozheniyu tochki O2 na nomogramme opredelyayutsya 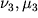 (v rassmatrivaemom primere dlya vtoroi krivoi tipa
(v rassmatrivaemom primere dlya vtoroi krivoi tipa 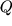 eti parametry opredelyayutsya po shkalam:
eti parametry opredelyayutsya po shkalam: 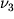 po
po 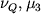 po
po 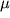 .
. - S dvuhsloinoi krivoi sovmeshaetsya chetvertaya vetv' (IV - V), i na blank perenositsya krest paletki O4 (
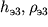 ), a po polozheniyu tochki O3 na nomogramme opredelyayutsya parametry
), a po polozheniyu tochki O3 na nomogramme opredelyayutsya parametry 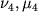 (v rassmatrivaemom primere dlya tret'ei krivoi tipa
(v rassmatrivaemom primere dlya tret'ei krivoi tipa 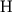 eti parametry opredelyayutsya po sleduyushim shkalam:
eti parametry opredelyayutsya po sleduyushim shkalam: 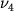 po
po 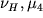 po
po 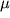 .
.
V rezul'tate interpretacii s pomosh'yu nomogrammy-paletki poluchayutsya te zhe parametry, chto i pri paletochnoi (sm. 3.12).
Parametry ![]() opredelyayutsya po formulam (3.12) i yavlyayutsya priblizhennymi. Dlya tochnogo ih opredeleniya neobhodima dopolnitel'naya informaciya, naprimer, znacheniya
opredelyayutsya po formulam (3.12) i yavlyayutsya priblizhennymi. Dlya tochnogo ih opredeleniya neobhodima dopolnitel'naya informaciya, naprimer, znacheniya ![]() i t.p. po dannym geofizicheskih issledovanii skvazhin. V privedennom primere (ris. 3.10) rezul'taty interpretacii sleduyushie (
i t.p. po dannym geofizicheskih issledovanii skvazhin. V privedennom primere (ris. 3.10) rezul'taty interpretacii sleduyushie (![]() v metrah,
v metrah, ![]() v Omm):
v Omm): ![]() m (s pomosh'yu primenennogo vyshe metoda
m (s pomosh'yu primenennogo vyshe metoda ![]()
![]() .
.
3. Mashinnye metody interpretacii. Interpretaciya EMZ s pomosh'yu EVM proizvoditsya s bol'shei tochnost'yu, ob'ektivnost'yu i skorost'yu. Sushestvuet mnozhestvo algoritmov resheniya obratnoi zadachi EMZ. Naibol'shee rasprostranenie poluchili algoritmy raznyh variantov podbora. Principy ih osnovany na sleduyushem.
- V hode predvaritel'noi interpretacii (kachestvennoi, a luchshe s pomosh'yu nomogramm-paletok) poluchaetsya apriornaya informaciya o geoelektricheskom razreze: chislo sloev, primernye znacheniya moshnostei i soprotivlenii.
- Vybirayutsya te ili inye metody i programmy resheniya pryamyh zadach EMZ, kotorye otlichayutsya tochnost'yu i vremenem scheta, etapami vvoda dopolnitel'noi informacii, vozmozhnost'yu ispol'zovat' razlichnye personal'nye komp'yutery i dr. Dlya polucheniya apriornyh parametrov modeli reshaetsya pryamaya zadacha i teoreticheskaya krivaya sravnivaetsya s polevoi.
- Dobivayutsya nailuchshego sovpadeniya polevoi krivoi s teoreticheskimi, u kotoryh postepenno menyayutsya parametry. Metodom posledovatel'nyh priblizhenii poluchayut minimum srednekvadraticheskogo otkloneniya ili logarifmicheskoi nevyazki kazhushihsya soprotivlenii na vseh parametrah glubinnosti.
- V minimiziruemyi funkcional nevyazki vvoditsya stabilizator resheniya s uchetom vseh dopolnitel'nyh geologo-geofizicheskih svedenii o raione issledovanii: minimal'nye i maksimal'nye moshnosti, elektromagnitnye svoistva sloev i t.d.
- Vydayutsya naibolee veroyatnye znacheniya parametrov geoelektricheskogo razreza (sm. 3.12), no bolee tochnye, chem rasschitannye po formulam (3.12) i (3.13), blagodarya ispol'zovaniyu dopolnitel'nyh dannyh.
|
Publikacii s klyuchevymi slovami:
geofizika - Zemlya - zemnaya kora
Publikacii so slovami: geofizika - Zemlya - zemnaya kora | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |