10.3. Principy resheniya pryamyh i obratnyh zadach seismorazvedki
10.3.1. Principy resheniya pryamyh zadach seismorazvedki.
Pryamoi zadachei seismorazvedki nazyvaetsya raschet vremen prihoda (![]() ) i amplitud (
) i amplitud (![]() ) dlya toi ili inoi volny dlya izvestnogo
seismogeologicheskogo razreza, t.e. kogda izvestny: moshnosti, glubiny
zaleganiya, razmery teh ili inyh geologicheskih ob'ektov (chashe sloev)
i skorosti raspredeleniya uprugih voln, a takzhe mesto i forma istochnika.
Strogoe reshenie pryamyh dinamicheskih zadach seismiki neodnorodnyh sred
proizvoditsya putem resheniya volnovogo uravneniya vida:
) dlya toi ili inoi volny dlya izvestnogo
seismogeologicheskogo razreza, t.e. kogda izvestny: moshnosti, glubiny
zaleganiya, razmery teh ili inyh geologicheskih ob'ektov (chashe sloev)
i skorosti raspredeleniya uprugih voln, a takzhe mesto i forma istochnika.
Strogoe reshenie pryamyh dinamicheskih zadach seismiki neodnorodnyh sred
proizvoditsya putem resheniya volnovogo uravneniya vida:
| (4.4) |
gde ![]() - skorost' toi ili inoi volny (
- skorost' toi ili inoi volny (![]() ili
ili ![]() ),
), ![]() - amplituda ili inoe vozmushenie signala, rasprostranyayusheesya
v srede (
- amplituda ili inoe vozmushenie signala, rasprostranyayusheesya
v srede (![]() ) na raznyh vremenah
) na raznyh vremenah ![]() posle ego vozbuzhdeniya. Reshenie etogo uravneniya s ispol'zovaniem granichnyh uslovii ochen' slozhno i ego udaetsya vypolnit' lish' dlya prostyh
modelei sred. Znachitel'no proshe reshat' kinematicheskie zadachi, t.e.
opredelyat' vremya prihoda toi ili inoi volny (pryamoi, otrazhennoi,
prelomlennoi i dr.) dlya izvestnoi modeli, znaya lish' polozhenie istochnika
i moment vozbuzhdeniya uprugoi volny. Tradicionno prosteishim rezul'tatom
resheniya pryamoi zadachi yavlyaetsya poluchenie uravneniya godografa, ili
analiticheskogo vyrazheniya dlya
posle ego vozbuzhdeniya. Reshenie etogo uravneniya s ispol'zovaniem granichnyh uslovii ochen' slozhno i ego udaetsya vypolnit' lish' dlya prostyh
modelei sred. Znachitel'no proshe reshat' kinematicheskie zadachi, t.e.
opredelyat' vremya prihoda toi ili inoi volny (pryamoi, otrazhennoi,
prelomlennoi i dr.) dlya izvestnoi modeli, znaya lish' polozhenie istochnika
i moment vozbuzhdeniya uprugoi volny. Tradicionno prosteishim rezul'tatom
resheniya pryamoi zadachi yavlyaetsya poluchenie uravneniya godografa, ili
analiticheskogo vyrazheniya dlya ![]() s dal'neishim postroeniem
godografa - grafika zavisimosti vremeni prihoda toi ili inoi
volny (
s dal'neishim postroeniem
godografa - grafika zavisimosti vremeni prihoda toi ili inoi
volny (![]() ) ot rasstoyaniya ot punkta vozbuzhdeniya do punkta priema (
) ot rasstoyaniya ot punkta vozbuzhdeniya do punkta priema (![]() ).
).
Samoi prostoi pryamoi zadachei seismorazvedki yavlyaetsya
poluchenie godografa pryamoi volny, t.e. zadachi, kotoruyu v drugih geofizicheskih
metodah nazyvayut zadachei o normal'nom pole (sm. ris. 4.2). Ochevidno,
chto vremya prihoda pryamoi volny posle sozdaniya uprugogo impul'sa v
punkte vozbuzhdeniya ili vzryva (PV) ravno ![]() . Poetomu lineinyi godograf imeet vid pryamoi linii. Po naklonu pryamoi linii mozhno opredelit' skorost'
. Poetomu lineinyi godograf imeet vid pryamoi linii. Po naklonu pryamoi linii mozhno opredelit' skorost' ![]() .
.
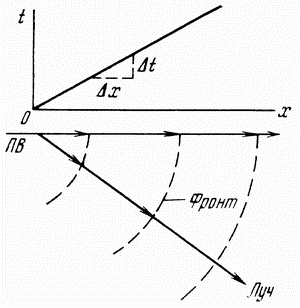 |
| Ris. 4.2. K vyvodu uravneniya pryamoi volny |
10.3.2. Pryamaya i obratnaya zadacha otrazhennoi volny dlya dvuhsloinoi sredy s naklonnoi granicei razdela.
1. Pryamaya zadacha. Pryamaya zadacha seismorazvedki metodom otrazhennyh voln (MOV) svoditsya k polucheniyu uravneniya godografa nad razrezom s izvestnymi moshnostyami sloev i skorostyami rasprostraneniya voln. Prosteishim yavlyaetsya dvuhsloinyi razrez s odnorodnym izotropnym verhnim sloem i skachkom akusticheskoi zhestkosti na naklonnoi granice s podstilayushim poluprostranstvom.
Pust' pod odnorodnoi pokryvayushei sredoi so skorost'yu
rasprostraneniya uprugih voln![]() raspolozhena vtoraya
sreda so skorost'yu
raspolozhena vtoraya
sreda so skorost'yu ![]() , a ugol razdelyayushei ih ploskoi
granicy raven
, a ugol razdelyayushei ih ploskoi
granicy raven ![]() (ris. 4.3). Esli na granice razdela
sred vypolnyaetsya uslovie
(ris. 4.3). Esli na granice razdela
sred vypolnyaetsya uslovie ![]() , to
obrazuetsya odnokratnaya otrazhennaya volna s uglom otrazheniya \gamma,
ravnym uglu padeniya
, to
obrazuetsya odnokratnaya otrazhennaya volna s uglom otrazheniya \gamma,
ravnym uglu padeniya ![]() . Trebuetsya naiti uravnenie
godografa, t.e. ustanovit' teoreticheskuyu zavisimost' vremeni prihoda
volny
. Trebuetsya naiti uravnenie
godografa, t.e. ustanovit' teoreticheskuyu zavisimost' vremeni prihoda
volny ![]() ot rasstoyaniya
ot rasstoyaniya ![]() , skorosti rasprostraneniya
volny v perekryvayushem sloe
, skorosti rasprostraneniya
volny v perekryvayushem sloe ![]() , eho-glubiny (glubiny
po normali k otrazhayushei granice) zaleganiya otrazhayushego kontakta
N i ego ugla naklona
, eho-glubiny (glubiny
po normali k otrazhayushei granice) zaleganiya otrazhayushego kontakta
N i ego ugla naklona ![]() .
.
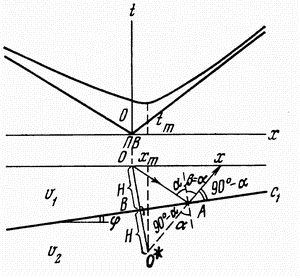 |
| Ris. 4.3. K vyvodu uravneniya godografa otrazhennoi volny nad dvuhsloinym razrezom |
Vremya prihoda otrazhennoi volny v tochku ![]() profilya nablyudeniya ravno
profilya nablyudeniya ravno ![]() . Pust' O^{*} - mnimyi punkt vzryva, ili tochka, raspolozhennaya na perpendikulyare k granice tak, chto
. Pust' O^{*} - mnimyi punkt vzryva, ili tochka, raspolozhennaya na perpendikulyare k granice tak, chto ![]() . Tak kak treugol'niki
. Tak kak treugol'niki ![]() i
i ![]() ravny, a
ravny, a ![]() i
i ![]() , to otrezki
, to otrezki ![]() i
i ![]() lezhat na odnoi linii i
lezhat na odnoi linii i
Iz pryamougol'nogo treugol'nika ![]() imeem
imeem
Itak,
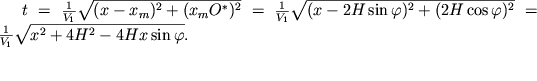 |
Eto i est' uravnenie lineinogo godografa odnokratno otrazhennoi volny.
Mozhno pokazat', chto poluchennoe uravnenie yavlyaetsya uravneniem giperboly. V samom dele, iz uravneniya godografa mozhno poluchit'
Eto giperbola, deistvitel'naya os' kotoroi parallel'na osi ![]() i smeshena na
i smeshena na ![]() po osi
po osi ![]() .
.
Iz uravneniya godografa mozhno naiti ego harakternye tochki:
Legko pokazat', chto pri ![]() godograf otrazhennoi
volny asimptoticheski priblizhaetsya k godografu pryamoi volny.
godograf otrazhennoi
volny asimptoticheski priblizhaetsya k godografu pryamoi volny.
Esli v uravnenii godografa dlya tochek profilya, raspolozhennyh
ot punkta vozbuzhdeniya po vosstaniyu plasta, pri vyrazhenii ![]() stoit znak "minus", to, kak legko pokazat', dlya tochek po padeniyu plasta dolzhen stoyat' znak "plyus".
stoit znak "minus", to, kak legko pokazat', dlya tochek po padeniyu plasta dolzhen stoyat' znak "plyus".
Takim obrazom, reshenie pryamoi zadachi metoda otrazhennyh voln dlya dvuhsloinogo odnorodnogo razreza privodit k sleduyushemu uravneniyu godografa:
| (4.6) |
2. Obratnaya zadacha. Obratnaya zadacha metoda
otrazhennyh voln (MOV) dlya modeli naklonnogo kontakta dvuh sred svoditsya
k opredeleniyu skorosti v perekryvayushem sloe ![]() (v metode MOV etu skorost' dlya sloistoi sredy nazyvayut effektivnoi
(v metode MOV etu skorost' dlya sloistoi sredy nazyvayut effektivnoi
![]() ) i geometricheskih parametrov razreza (
) i geometricheskih parametrov razreza (![]() ). Obratnaya zadacha reshaetsya razlichnymi sposobami na osnove analiza uravneniya godografa (4.6).
). Obratnaya zadacha reshaetsya razlichnymi sposobami na osnove analiza uravneniya godografa (4.6).
Rassmotrim prosteishie iz nih.
A. Opredelenie effektivnyh skorostei v perekryvayushei tolshe po godografam otrazhennyh voln sposobami postoyannoi raznosti i vstrechnyh godografov. Sposob postoyannoi raznosti pri obrabotke odinochnyh godografov. Vzyav dve tochki godografa, udalennye na rasstoyanie m, zapishem, ispol'zuya (4.6), dlya nih uravneniya:
Vychtya iz vtorogo uravneniya pervoe i oboznachiv ![]() , poluchim:
, poluchim:
Otsyuda, polozhiv ![]() , mozhno naiti
, mozhno naiti ![]() kak uglovoi koefficient pryamoi v novoi sisteme koordinat
kak uglovoi koefficient pryamoi v novoi sisteme koordinat ![]() i
i ![]() . V samom dele, prodifferencirovav eto uravnenie, poluchim
. V samom dele, prodifferencirovav eto uravnenie, poluchim ![]() . Uchtya, chto dlya pryamoi
linii
. Uchtya, chto dlya pryamoi
linii ![]() , legko poluchit' formulu dlya rascheta:
, legko poluchit' formulu dlya rascheta:
| (4.7) |
Pri prakticheskom primenenii poluchennoi formuly
postupayut sleduyushim obrazom. Na godografe vybiraetsya neskol'ko par
tochek (![]() i
i ![]() i
i ![]() i
i ![]() ), raspolozhennyh na postoyannom rasstoyanii m drug ot druga. Dlya kazhdoi pary
vremen nahoditsya funkciya
), raspolozhennyh na postoyannom rasstoyanii m drug ot druga. Dlya kazhdoi pary
vremen nahoditsya funkciya ![]() ,
sootvetstvuyushaya znacheniyu
,
sootvetstvuyushaya znacheniyu ![]() , i stroitsya grafik funkcii
, i stroitsya grafik funkcii ![]() ot
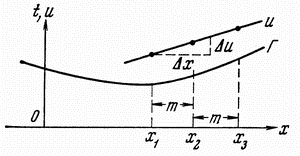
ot ![]() (ris. 4.4). Vzyav prirashenie
(ris. 4.4). Vzyav prirashenie ![]() dlya kakogo-to
dlya kakogo-to ![]() , legko rasschitat'
, legko rasschitat' ![]() po formule (4.7).
po formule (4.7).
 |  |
| a | b |
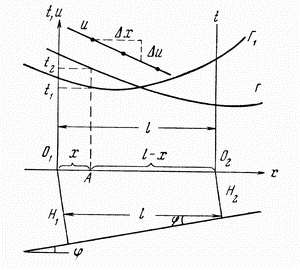
| Ris. 4.4. Opredelenie effektivnoi skorosti po dannym MOV sposobom postoyannoi raznosti (a) i vstrechnyh godografov (b) | |
Sposob dvuh vstrechnyh godografov. Esli est' dva vstrechnyh godografa (ris. 4.4, b), to uravneniya godografov dlya odnoi tochki profilya imeyut vid
Vychtya iz vtorogo uravneniya pervoe i uchtya, chto ![]() , poluchim
, poluchim
Vvedya oboznacheniya ![]() i zameniv vse chleny pravoi chasti, ne soderzhashie
i zameniv vse chleny pravoi chasti, ne soderzhashie ![]() , na
, na ![]() , mozhno zapisat':
, mozhno zapisat':
Poslednee uravnenie yavlyaetsya uravneniem pryamoi
v sisteme koordinat ![]() .
.
Otsyuda:
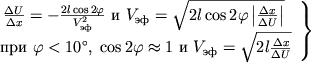 | (4.8) |
Prakticheskoe primenenie etoi
formuly svoditsya k postroeniyu pryamoi linii v koordinatah (![]() ) i opredeleniyu
) i opredeleniyu ![]() po uglovomu koefficientu
etoi linii
po uglovomu koefficientu
etoi linii ![]() .
.
|
Publikacii s klyuchevymi slovami:
geofizika - Zemlya - zemnaya kora
Publikacii so slovami: geofizika - Zemlya - zemnaya kora | |
|
Sm. takzhe:
| |