B. Sposoby postroeniya otrazhayushih granic. Poluchiv
Naibolee prostymi sposobami
postroeniya otrazhayushih granic yavlyayutsya razlichnye graficheskie varianty:
sposob ![]() , sposob zasechek, sposob ellipsov i dr.
, sposob zasechek, sposob ellipsov i dr.
Sposob ![]() . Poskol'ku
. Poskol'ku ![]() , gde
, gde ![]() - vremya na punkte vzryva, kotoroe mozhno opredelit' po godografu (ono ravno vremeni pri
- vremya na punkte vzryva, kotoroe mozhno opredelit' po godografu (ono ravno vremeni pri ![]() ), to glubina zaleganiya ravna
), to glubina zaleganiya ravna ![]() .
.
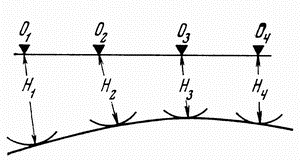
Imeya neskol'ko PV (neskol'ko godografov), mozhno postroit' otrazhayushuyu granicu kak kasatel'nuyu k
okruzhnostyam s radiusami ![]() , provedennymi iz sootvetstvuyushih PV (ris. 4.5, a).
, provedennymi iz sootvetstvuyushih PV (ris. 4.5, a).
 |  |  |
| a | b | v |
| Ris. 4.5. Postroenie otrazhayushei granicy sposobami: a - | ||
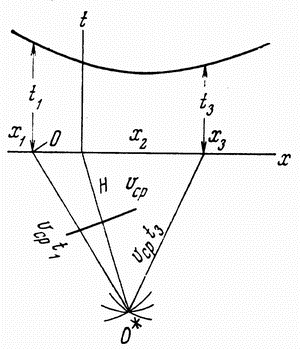
Sposob zasechek. Na profile nablyudenii vybirayut
3 - 5 tochek i iz nih provodyat zasechki radiusami ![]() . Zasechki, peresekayas' primerno v odnoi tochke, dayut mestopolozhenie mnimogo punkta vzryva
. Zasechki, peresekayas' primerno v odnoi tochke, dayut mestopolozhenie mnimogo punkta vzryva ![]() , a otrazhayushaya granica raspolagaetsya v seredine i perpendikulyarno
, a otrazhayushaya granica raspolagaetsya v seredine i perpendikulyarno ![]() (ris. 4.5, b).
(ris. 4.5, b).
Sposob ellipsov. V sluchae neploskih granic razdela dlya postroeniya otrazhayushei granicy
primenyaetsya sposob ellipsov. Izvestno, chto ellips - eto krivaya,
kazhdaya tochka kotoroi raspolozhena na postoyannoi summe rasstoyanii do
dvuh ego fokusov. Prinyav ![]() i
i ![]() za fokusy
ellipsa s postoyannym rasstoyaniem
za fokusy
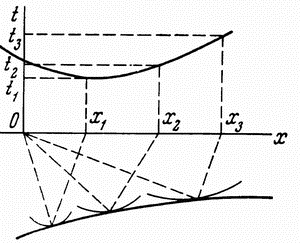
ellipsa s postoyannym rasstoyaniem ![]() , legko videt', chto otrazhayushaya ploshadka
lezhit na ellipse (ris. 4.5, v). Postroit' ukazannyi ellips
mozhno sleduyushim obrazom. Beretsya nit' dlinoi
, legko videt', chto otrazhayushaya ploshadka
lezhit na ellipse (ris. 4.5, v). Postroit' ukazannyi ellips
mozhno sleduyushim obrazom. Beretsya nit' dlinoi ![]() (velichina
(velichina ![]() vybiraetsya v tom zhe masshtabe, v kotorom stroitsya razrez). Ee koncy zakreplyayutsya knopkoi v tochkah
vybiraetsya v tom zhe masshtabe, v kotorom stroitsya razrez). Ee koncy zakreplyayutsya knopkoi v tochkah ![]() i
i ![]() . Natyagivaya nit' karandashom, legko prochertit' ellips. Postroiv analogichnye ellipsy dlya ryada godografov, mozhno postroit'
otrazhayushuyu granicu, kotoroi yavlyaetsya ogibayushaya vseh ellipsov.
. Natyagivaya nit' karandashom, legko prochertit' ellips. Postroiv analogichnye ellipsy dlya ryada godografov, mozhno postroit'
otrazhayushuyu granicu, kotoroi yavlyaetsya ogibayushaya vseh ellipsov.
Privedennyi primer resheniya pryamoi i obratnoi zadachi MOV nad dvuhsloinym razrezom mozhno perenesti i na mnogosloinyi razrez, esli zamenit' sloi s ![]() na mnogosloinuyu tolshu s nekotoroi srednei ili effektivnoi skorost'yu i toi zhe moshnost'yu
na mnogosloinuyu tolshu s nekotoroi srednei ili effektivnoi skorost'yu i toi zhe moshnost'yu ![]() . Dlya etogo v formulah 4.5 - 4.7 sleduet zamenit'
. Dlya etogo v formulah 4.5 - 4.7 sleduet zamenit' ![]() na
na ![]() (sm. 12.2).
(sm. 12.2).
10.3.3. Pryamaya i obratnaya zadacha golovnoi prelomlennoi volny dlya dvuhsloinoi sredy s ploskoi naklonnoi granicei razdela.
1. Obrazovanie golovnoi prelomlennoi volny. Kak otmechalos' vyshe (sm. 10.1.4), pri kriticheskom ugle padeniya ![]() , kogda ugol prelomleniya \beta raven 90
, kogda ugol prelomleniya \beta raven 90![]() , vdol' granicy nachnet skol'zit' prelomlennaya volna, kotoraya voznikaet pri
, vdol' granicy nachnet skol'zit' prelomlennaya volna, kotoraya voznikaet pri ![]() , tak kak
, tak kak ![]() .
.
Pri padenii pryamoi sfericheskoi volny pod kriticheskim uglom ![]() v tochke
v tochke ![]() (ris. 4.6) obrazuyutsya dve volny: odna otrazhennaya, dvizhushayasya po luchu
(ris. 4.6) obrazuyutsya dve volny: odna otrazhennaya, dvizhushayasya po luchu ![]() so skorost'yu
so skorost'yu ![]() , i vtoraya, skol'zyashaya vdol' granicy razdela so skorost'yu
, i vtoraya, skol'zyashaya vdol' granicy razdela so skorost'yu ![]() (
(![]() , kak pravilo, ravno
, kak pravilo, ravno ![]() ). Chtoby pokazat', kak eta skol'zyashaya prelomlennaya volna vyhodit na liniyu nablyudenii (os'
). Chtoby pokazat', kak eta skol'zyashaya prelomlennaya volna vyhodit na liniyu nablyudenii (os' ![]() ), vospol'zuemsya principom Gyuigensa.
), vospol'zuemsya principom Gyuigensa.
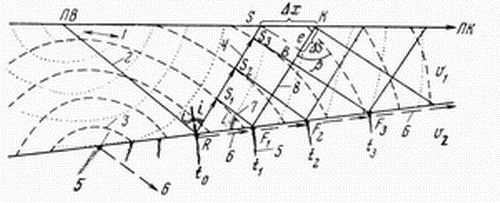 |
| Ris. 4.6. Priroda obrazovaniya seismicheskih voln: 1, 2 - front i luch pryamoi volny; 3, 4 - front i luch otrazhennoi volny; 5, 6 - front i luch prelomlennoi prohodyashei volny; 7, 8 - front i luch golovnoi prelomlennoi volny |
Soglasno principu Gyuigensa, lyubaya tochka fronta volny yavlyaetsya istochnikom kolebanii. V chastnosti, iz tochki ![]() nachnet rasprostranyat'sya front otrazhennoi volny so skorost'yu
nachnet rasprostranyat'sya front otrazhennoi volny so skorost'yu
![]() , kotoryi cherez vremya
, kotoryi cherez vremya ![]() posle nachala otrazheniya dostignet tochki
posle nachala otrazheniya dostignet tochki ![]() . Za eto zhe vremya v srede
. Za eto zhe vremya v srede ![]() front prohodyashei prelomlennoi
volny, perpendikulyarnyi granice razdela, dostignet tochki
front prohodyashei prelomlennoi
volny, perpendikulyarnyi granice razdela, dostignet tochki ![]() . Sootvetstvenno za vremya
. Sootvetstvenno za vremya ![]() fronty etih voln dostignut tochek
fronty etih voln dostignut tochek ![]() , za vremya
, za vremya ![]() i tak dalee. Poskol'ku
i tak dalee. Poskol'ku ![]() , prelomlennaya volna rasprostranyaetsya bystree otrazhennoi.
, prelomlennaya volna rasprostranyaetsya bystree otrazhennoi.
Front prohodyashei prelomlennoi volny, skol'zya vdol'
granicy razdela, vozbuzhdaet v verhnem sloe kolebaniya, kotorye i vyzyvayut
poyavlenie tak nazyvaemoi golovnoi prelomlennoi volny. V samom dele,
za vremya ![]() , oblast' vozmushenii v verhnei srede budet zaklyuchena v treugol'nike
, oblast' vozmushenii v verhnei srede budet zaklyuchena v treugol'nike ![]() ; za vremya
; za vremya ![]() oblast' vozmushenii
budet zaklyuchena v treugol'nike
oblast' vozmushenii
budet zaklyuchena v treugol'nike ![]() i tak dalee. Front nekotoroi novoi volny, nazyvaemoi golovnoi, otdelyayushei oblast' prostranstva, vozmushennuyu uprugimi kolebaniyami,
ot nevozmushennoi, v moment
i tak dalee. Front nekotoroi novoi volny, nazyvaemoi golovnoi, otdelyayushei oblast' prostranstva, vozmushennuyu uprugimi kolebaniyami,
ot nevozmushennoi, v moment ![]() budet prohodit'
vdol' pryamoi linii
budet prohodit'
vdol' pryamoi linii ![]() , v moment
, v moment ![]() - vdol' linii
- vdol' linii ![]() i tak dalee. Odnoi storonoi front golovnoi volny
kasaetsya fronta otrazhennoi iz kriticheskoi tochki volny, drugoi primykaet
k frontu skol'zyashei prelomlennoi volny. V tochke
i tak dalee. Odnoi storonoi front golovnoi volny
kasaetsya fronta otrazhennoi iz kriticheskoi tochki volny, drugoi primykaet
k frontu skol'zyashei prelomlennoi volny. V tochke ![]() , gde voznikaet
golovnaya volna, fronty otrazhennoi i golovnoi voln vyidut na poverhnost'
odnovremenno, a dalee otrazhennaya volna, poskol'ku ona imeet men'shuyu
skorost', nachnet otstavat' ot golovnoi.
, gde voznikaet
golovnaya volna, fronty otrazhennoi i golovnoi voln vyidut na poverhnost'
odnovremenno, a dalee otrazhennaya volna, poskol'ku ona imeet men'shuyu
skorost', nachnet otstavat' ot golovnoi.
Iz ris. 4.6 vidno, chto fronty golovnoi prelomlennoi
volny budut ploskostyami, naklonennymi pod uglom ![]() k granice
razdela, a luchi, perpendikulyarnye frontu, budut nakloneny pod postoyannym
uglom e k poverhnosti nablyudenii. Front golovnoi volny budet
skol'zit' vdol' linii nablyudenii s kazhusheisya skorost'yu
k granice
razdela, a luchi, perpendikulyarnye frontu, budut nakloneny pod postoyannym
uglom e k poverhnosti nablyudenii. Front golovnoi volny budet
skol'zit' vdol' linii nablyudenii s kazhusheisya skorost'yu ![]() . Iz treugol'nika
. Iz treugol'nika ![]() legko poluchit' vyrazhenie dlya kazhusheisya skorosti (zakon
kazhushihsya skorostei, zakon Benndorfa). V samom dele,
legko poluchit' vyrazhenie dlya kazhusheisya skorosti (zakon
kazhushihsya skorostei, zakon Benndorfa). V samom dele, ![]() , otsyuda
, otsyuda ![]() , t.e. dlya dannoi sredy
, t.e. dlya dannoi sredy ![]() .
.
Ustanovim svyaz' mezhdu uglom vyhoda seismicheskoi
radiacii ![]() i uglami
i uglami ![]() i
i ![]() . Ugol
. Ugol ![]() na ris. 4.7 raven uglu
na ris. 4.7 raven uglu ![]() , a poslednii raven
, a poslednii raven ![]() (kak ugly so vzaimnoperpendikulyarnymi storonami).
Poetomu
(kak ugly so vzaimnoperpendikulyarnymi storonami).
Poetomu ![]() , otsyuda
, otsyuda ![]() .
.
Indeks "B" vzyat dlya znachenii ![]() i
i ![]() po vosstaniyu plasta. Esli indeksom "P" oboznachit' sootvetstvuyushie znacheniya po padeniyu plasta, to netrudno dokazat', chto
po vosstaniyu plasta. Esli indeksom "P" oboznachit' sootvetstvuyushie znacheniya po padeniyu plasta, to netrudno dokazat', chto ![]() . Tochki
. Tochki ![]() i
i ![]() yavlyayutsya nachal'nymi tochkami prelomlennoi volny. Mezhdu nimi prelomlennye volny nablyudat'sya ne mogut, t.e. oni vyhodyat na zemnuyu poverhnost' na nekotorom rasstoyanii ot punkta vzryva, sravnimom s glubinoi zaleganiya prelomlyayushei granicy.
yavlyayutsya nachal'nymi tochkami prelomlennoi volny. Mezhdu nimi prelomlennye volny nablyudat'sya ne mogut, t.e. oni vyhodyat na zemnuyu poverhnost' na nekotorom rasstoyanii ot punkta vzryva, sravnimom s glubinoi zaleganiya prelomlyayushei granicy.
2. Vyvod uravneniya lineinogo godografa golovnoi prelomlennoi volny, obrazovavsheisya nad naklonnoi granicei dvuh sred (pryamaya zadacha). Pust' pod odnorodnoi pokryvayushei
sredoi so skorost'yu rasprostraneniya uprugih voln ![]() raspolozhena ploskaya granica vtorogo sloya s
raspolozhena ploskaya granica vtorogo sloya s ![]() . Trebuetsya poluchit' uravnenie godografa
golovnoi prelomlennoi volny, t.e. ustanovit' teoreticheskuyu zavisimost'
vremeni prihoda volny (
. Trebuetsya poluchit' uravnenie godografa
golovnoi prelomlennoi volny, t.e. ustanovit' teoreticheskuyu zavisimost'
vremeni prihoda volny (![]() ) ot rasstoyaniya (
) ot rasstoyaniya (![]() ), skorosti
rasprostraneniya uprugih voln (
), skorosti
rasprostraneniya uprugih voln (![]() i
i ![]() ), glubiny zaleganiya (
), glubiny zaleganiya (![]() ) i ugla naklona (
) i ugla naklona (![]() ) prelomlyayushei granicy (ris. 4.7).
) prelomlyayushei granicy (ris. 4.7).
Kak pokazano vyshe, pervoi tochkoi profilya nablyudenii,
v kotoroi nachinaet registrirovat'sya prelomlennaya volna, yavlyaetsya
tochka ![]() , nazyvaemaya
nachal'noi tochkoi golovnoi volny. Tak kak vse luchi golovnoi prelomlennoi
volny parallel'ny, to ugly
, nazyvaemaya
nachal'noi tochkoi golovnoi volny. Tak kak vse luchi golovnoi prelomlennoi
volny parallel'ny, to ugly ![]() i
i ![]() postoyanny, a eto znachit, chto lineinyi godograf prelomlennoi volny imeet postoyannyi naklon k osi
postoyanny, a eto znachit, chto lineinyi godograf prelomlennoi volny imeet postoyannyi naklon k osi ![]() . Naklon
k osi h ostaetsya postoyannym lish' u pryamoi linii. Takim obrazom,
godograf golovnoi prelomlennoi volny nad ploskoi granicei yavlyaetsya
pryamoi liniei, nachinayusheisya v tochke
. Naklon
k osi h ostaetsya postoyannym lish' u pryamoi linii. Takim obrazom,
godograf golovnoi prelomlennoi volny nad ploskoi granicei yavlyaetsya
pryamoi liniei, nachinayusheisya v tochke ![]() s koordinatami
s koordinatami ![]() i
i ![]() i naklonennoi k osi
i naklonennoi k osi ![]() pod uglom
pod uglom ![]() .
.
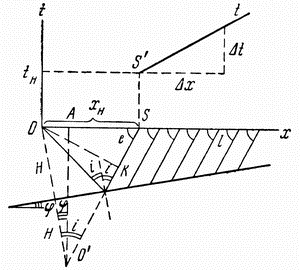 |
| Ris. 4.7. K vyvodu uravneniya godografa golovnoi prelomlennoi volny |
Otsyuda mozhno poluchit' uravnenie godografa prelomlennoi
volny. Po vosstaniyu plasta ![]() , gde
, gde ![]() i
i ![]() - koordinaty lyuboi tochki godografa. Ochevidno, dlya polucheniya uravneniya
neobhodimo opredelit'
- koordinaty lyuboi tochki godografa. Ochevidno, dlya polucheniya uravneniya
neobhodimo opredelit' ![]() i
i ![]() .
.
Voz'mem mnimyi punkt vzryva ![]() i opustim perpendikulyary na O'A i os'
i opustim perpendikulyary na O'A i os' ![]() . Iz treugol'nika
. Iz treugol'nika ![]()
![]() , iz treugol'nika OO'K OK = 2H sin i. Uchityvaya, chto
, iz treugol'nika OO'K OK = 2H sin i. Uchityvaya, chto ![]() , poluchim
, poluchim
Iz treugol'nika O'AS i OO'A mozhno poluchit' ![]() i
i ![]() . Otkuda
. Otkuda ![]() . Netrudno pokazat', chto dlya tochek po padeniyu granicy
. Netrudno pokazat', chto dlya tochek po padeniyu granicy
Uchityvaya, chto ![]() , poluchaem uravnenie godografa
prelomlennoi volny:
, poluchaem uravnenie godografa
prelomlennoi volny:
Provedya preobrazovaniya vo vtorom slagaemom, mozhno poluchit' okonchatel'noe uravnenie godografa prelomlennoi volny:
| (4.9) |
Prichem znak "-" beretsya dlya godografa po vosstaniyu granicy (zdes' volna prihodit bystree), znak
"+" beretsya dlya godografa po padeniyu granicy ot punkta vzryva. Iz
uravnenii godografov vidno, chto pri ![]() , gde
, gde
![]() - vremya na punkte vzryva.
- vremya na punkte vzryva.
Dlya gorizontal'noi prelomlyayushei granicy (![]() )
)
| (4.10) |
Vyrazhenie dlya godografa prelomlennoi volny mozhno zapisat' v takom vide:
Pri ![]() , chto oznachaet prihod volny snachala k udalennym, a zatem
k blizkim k punktu vzryva tochkam nablyudeniya. Pri
, chto oznachaet prihod volny snachala k udalennym, a zatem
k blizkim k punktu vzryva tochkam nablyudeniya. Pri ![]() i
i
![]() , chto sootvetstvuet sluchayu, kogda golovnaya
prelomlennaya volna ne smozhet vyiti na poverhnost' i raboty metodom
MPV nevozmozhny. Poetomu etot metod mozhet primenyat'sya dlya izucheniya
ne ochen' krutyh struktur, t.e. pri uglah padeniya, men'shih 45
, chto sootvetstvuet sluchayu, kogda golovnaya
prelomlennaya volna ne smozhet vyiti na poverhnost' i raboty metodom
MPV nevozmozhny. Poetomu etot metod mozhet primenyat'sya dlya izucheniya
ne ochen' krutyh struktur, t.e. pri uglah padeniya, men'shih 45![]() .
.
Prelomlennaya volna na udalenii ![]() ot punkta vzryva vsegda prihodit ran'she otrazhennoi i pryamoi voln i ee udobno registrirovat' v oblasti pervyh vstuplenii.
Primenyaetsya takzhe korrelyacionnyi metod prelomlennyh voln (KMPV),
kogda vydelenie prelomlennyh voln proizvoditsya i v posleduyushih vstupleniyah.
ot punkta vzryva vsegda prihodit ran'she otrazhennoi i pryamoi voln i ee udobno registrirovat' v oblasti pervyh vstuplenii.
Primenyaetsya takzhe korrelyacionnyi metod prelomlennyh voln (KMPV),
kogda vydelenie prelomlennyh voln proizvoditsya i v posleduyushih vstupleniyah.
Kak pokazano vyshe, godograf volny, prelomlennoi na ploskoi granice dvuh sred, pryamolineen. Odnako, esli prelomlyayushaya granica krivolineina, to i godograf priobretaet krivolineinuyu formu. Eto ob'yasnyaetsya tem, chto ugol vyhoda seismicheskoi radiacii ![]() i kazhushayasya skorost'
i kazhushayasya skorost' ![]() menyaetsya pri izmenenii ugla naklona
granicy (
menyaetsya pri izmenenii ugla naklona
granicy (![]() ) po profilyu nablyudenii, chto privodit k izmeneniyu ugla naklona godografa.
) po profilyu nablyudenii, chto privodit k izmeneniyu ugla naklona godografa.
Kak otmechalos' v 10.1.4, esli v srede skorost' uprugih voln vozrastaet s glubinoi, chto mozhet nablyudat'sya, naprimer, pri smene litologii ili iz-za uvelicheniya davleniya, to voznikayut refragirovannye volny. Mehanizmy obrazovaniya refragirovannyh i skol'zyashih prelomlennyh voln imeyut opredelennoe shodstvo. S uvelicheniem skorosti s glubinoi kriticheskii ugol padeniya uvelichivaetsya i refragirovannye volny budut prohodit' vo vtorom sloe po dugoobraznym lucham (4.1, v). Vyhodya na poverhnost' zemli, refragirovannye volny registriruyutsya podobno golovnym prelomlennym. Godografy prelomlennyh i refragirovannyh voln shodny mezhdu soboi, i ih raspoznavanie imeet bol'shoe znachenie, tak kak pozvolyaet izbavit'sya ot oshibok pri interpretacii rezul'tatov seismorazvedki.
|
Publikacii s klyuchevymi slovami:
geofizika - Zemlya - zemnaya kora
Publikacii so slovami: geofizika - Zemlya - zemnaya kora | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |