Astronet > Geofizicheskie metody issledovaniya zemnoi kory. Chast' 1

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Geofizicheskie metody issledovaniya zemnoi kory

1.3. Principy resheniya pryamyh i obratnyh zadach gravirazvedki

V rezul'tate gravirazvedki rasschityvayutsya anomalii sily tyazhesti, obuslovlennye temi ili inymi plotnostnymi neodnorodnostyami, a vliyanie prityazheniya vsei Zemli i okruzhayushego rel'efa isklyuchaetsya vychitaniem normal'nogo polya i vvedeniem redukcii (sm. 1.2.3). Poetomu v matematicheskoi teorii gravirazvedki rascchityvayutsya anomalii ot tel prostyh form: shara, gorizontal'nogo cilindra, vertikal'nogo ustupa, vertikal'nogo cilindra i t.d. bez ucheta prityazheniya vsei Zemlei.

Nahozhdenie anomalii sily tyazhesti i vtoryh proizvodnyh potenciala ot tel izvestnoi formy, glubiny zaleganiya, razmera i plotnosti nosit nazvanie pryamoi zadachi gravirazvedki. Opredelenie mestopolozheniya, formy, glubiny zaleganiya, razmerov i plotnosti tel po izvestnym anomaliyam $\Delta g$ ili vtoryh proizvodnyh potenciala sily tyazhesti nazyvaetsya obratnoi zadachei gravirazvedki.

1.3.1. Analiticheskie sposoby resheniya pryamyh zadach gravirazvedki.

Anomaliya sily tyazhesti, vyzvannaya prityazheniem tel izvestnoi formy, razmera i plotnosti, mozhet byt' vychislena na osnovanii zakona vsemirnogo prityazheniya (zakon N'yutona).

Pust' v koordinatnoi sisteme xyz os' z napravlena vniz k centru Zemli. Stavitsya zadacha opredelit' v tochke nablyudeniya A(x,y,z) anomal'nuyu silu tyazhesti ( $\Delta g$ ), t.e. vertikal'nuyu sostavlyayushuyu sily prityazheniya Zemlei edinicy massy ( ) elementarnoi massoi dm, nahodyasheisya v tochke M (x',y',z') (ris. 1.2).

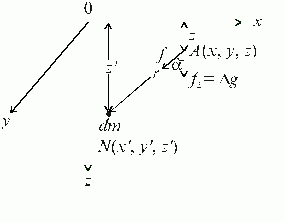Ris.1.2 K opredeleniyu anomalii sily tyazhesti ot elementarnoi massy

Po zakonu N'yutona prityazhenie edinichnoi massy ravno:

f=Gdm/r²,

gde $G$ - gravitacionnaya postoyannaya, $r$ - rasstoyanie mezhdu tochkami (sm. 1.4).

Anomaliya $\Delta g$ yavlyaetsya proekciei vektora f na os' z:
$\Delta g=f\cos\alpha =G \frac{dm}{{r}^{2}}\cdot\frac{({z'} -z)}{r},$ (1.6)

gde iz treugol'nika ABM $\cos\alpha=(z'-z)/r$ . Eto zhe vyrazhenie mozhno poluchit' s pomosh'yu potenciala W=Gdm/r. V samom dele:
$\Delta g=- \frac{\partial W}{\partial z} = \frac{Gdm({z'} -z)}{{r}^{3} }$ (1.7)

Oboznachiv plotnost' prityagivayushei massy cherez $\sigma$ , a ee ob'em cherez dV, mozhno zapisat'
$\Delta g=G \frac{dv}{{r}^{3}} ({z'} -z)$ (1.8)

Takova budet anomaliya sily tyazhesti, obuslovlennaya massoi, raspolozhennoi v pustote. V prirodnyh usloviyah anomal'nye vklyucheniya raspolozheny vo vmeshayushei srede s nekotoroi plotnost'yu $\sigma_{0}$ , poetomu pod massoi dm nado ponimat' izbytochnuyu massu $dm = (\sigma - \sigma_{0} )dV$ .

Otsyuda
$\Delta g=G(\sigma -{\sigma}_{o} ) \frac{dv}{{r}^{3} } ({z'} -z),$ (1.9)

gde $(\sigma - \sigma_{0} ) = \Delta\sigma$ - izbytochnaya plotnost'.

Pri $\sigma\gt\sigma_{0}$ $\Delta g$ imeet polozhitel'nyi znak, t.e. nablyudaetsya uvelichenie prityazheniya i polozhitel'nye anomalii $\Delta g$ . Pri $\sigma\lt\sigma_{0}$ $\Delta g$ imeet otricatel'nyi znak, t.e. nablyudaetsya umen'shenie prityazheniya i otricatel'nye anomalii $\Delta g$ .

V principe anomaliya, sozdannaya lyubym telom, mozhet byt' opredelena integralom po ob'emu tela:
$\Delta {g}_{v} =G(\sigma -{\sigma }_{o} ){\int }_{V} \frac{({z'} -z)dV}{{r}^{3} }$ (1.10)

t.e. summoi prityazhenii vseh elementarnyh ob'emov, iz kotoryh sostoit telo.

Rassmotrim neskol'ko pryamyh i obratnyh zadach dlya tel prostoi geometricheskoi formy.

1.3.2. Pryamaya i obratnaya zadachi nad sharom.

1. Pryamaya zadacha. Pust' odnorodnyi shar radiusa $a$ i plotnosti $\sigma$ raspolozhen na glubine $h$ v srede s plotnost'yu $\sigma_{0}$ (dlya prostoty centr nahoditsya na osi z, a nablyudeniya provodyatsya po osi x v tochke P) (ris. 1.3).

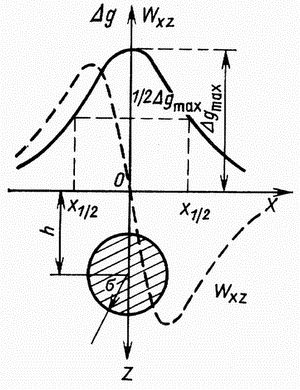Ris.1.3 Gravitacionnoe pole shara

Formula dlya vychisleniya $g$ mozhet byt' poluchena iz (1.6) - (1.9) putem zameny elementa $dm$ massoi shara v silu togo, chto prityazhenie odnorodnym sharom proishodit tak, kak esli by vsya massa byla sosredotochena v centre shara. Uchtya, chto x'=y'=0,z'=h,y=z=0, poluchim dlya shara
$\Delta g=GM \frac{h}{{r}^{3} } =G(\sigma -{\sigma }_{o} )V \frac{h}{{r}^{3} } =G(\sigma -{\sigma }_{o} )Vh/({x}^{2} +{h}^{2})^{3/2}$ (1.11)

Grafik $\Delta g$ budet imet' maksimum nad sharom (x=0) i asimptoticheski stremit'sya k nulyu pri udalenii ot shara. V plane izolinii $\Delta g$ budut imet' vid koncentricheskih okruzhnostei.

Vtoraya proizvodnaya (gradient anomalii po profilyu nablyudenii) ravna:
${W}_{xz} = \frac{\partial (\Delta g)}{\partial x} =GMh\partial (1/{r}^{3} )/\partial x=-3GMhx/{r}^{5}$

Vid krivoi W_xz mozhet byt' legko poluchen putem graficheskogo postroeniya iz krivoi $\Delta g$ . Grafik W_xz imeet pered sharom maksimum, za sharom - minimum, nad centrom shara - nol'.

2. Obratnaya zadacha. Iz (1.11) maksimum $\Delta g$ nad centrom shara (x=0) raven $\Delta g_{ max} = GM/ h^{ 2}$ .

Dlya tochki, udalennoi ot maksimuma na rasstoyanie x_1/2, imeyushei $\Delta g_{ 1/2}= 1/2 \Delta g_{ max}$ , mozhno zapisat' sleduyushee uravnenie:
$\Delta {g}_{1/2} = \frac{GM}{2{h}^{2} } = \frac{GMh}{({x}_{1/2}^{2} +{h}^{2} )^{3/2} }\; \hbox{ili} \; 2{h}^{3} =({x}_{1/2}^{2} +{h}^{2})^{3/2} .$

Reshiv poslednee uravnenie, poluchim formulu dlya opredeleniya glubiny zaleganiya centra shara h=1,3x_1/2. Znaya $h$ , legko naiti izbytochnuyu massu ( $M$ ): $M = \Delta g_{ max } h^{ 2}/G$ .

Tak kak $M=V ( \sigma - \sigma_{ 0}) = 4/3\pi a^{ 3} ( \sigma - \sigma_{0}),$ to, znaya izbytochnuyu plotnost' $( \sigma -\sigma_{ 0})$ , mozhno rasschitat' ob'em ( $V$ ) i radius shara ( $a$ ). Tak, radius raven:
$a = \sqrt[3]{ \frac{3M}{4\pi(\sigma -\sigma_{0} )} } =0,01 \sqrt[3]{0,38\Delta {g}_{\max } {h}^{2}/(\sigma -{\sigma }_{0} )},$

gde $\Delta g_{ max}$ - v milligalah, $h$ - v metrah, $( \sigma - \sigma_{0})$ - v tonnah / kub. metr (g/sm³).

1.3.3. Pryamaya i obratnaya zadachi nad gorizontal'nym beskonechno dlinnym krugovym cilindrom.

1.Pryamaya zadacha. Rassmotrim beskonechno dlinnyi krugovoi gorizontal'nyi cilindr radiusa $R$ , raspolozhennyi vdol' osi y (ris. 1.4). Os' nablyudenii ( x) napravim vkrest prostiraniya cilindra.

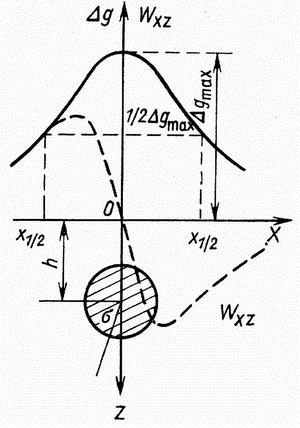Ris.1.4 Gravitacionnoe pole beskonechno dlinnogo krugovogo gorizontal'nogo cilindra

Prityazhenie odnorodnym cilindrom proishodit tak zhe, kak esli by vsya ego massa byla sosredotochena vdol' veshestvennoi linii, raspolozhennoi vdol' osi cilindra, s massoi edinicy dliny, ravnoi $\lambda = dm / dy = \pi R^{ 2}( \sigma - \sigma_{0})$ . Ispol'zuya (1.10), mozhno poluchit' formuly dlya $\Delta g$ i $W _{ xz }$ :
$\Delta g = Gh\lambda {\int\limits }_{-\infty }^{+\infty } \frac{dy}{({x}^{2} + {y}^{2} + {z}^{2} {)}^{3/2} } = \frac{2Gh\pi {R}^{2} (\sigma - {\sigma }_{o} )}{{x}^{2} + {h}^{2} } ,$ (1.12)

${W}_{xz} = \frac{\partial(\Delta g)}{\partial z}=-\frac{4Gh\lambda x}{(x^2+h^2)^2}.$

Grafiki $\Delta g$ i $W _{ xz}$ nad cilindrom i sharom vneshne pohozhi (sm. ris. 1.3 i 1.4). V plane izolinii $\Delta g$ nad cilindrom budut vytyanutymi parallel'nymi liniyami.

2. Obratnaya zadacha. Iz (1.10 i 1.12) mozhno pri h=0 poluchit' $\Delta g _{max} = 2 { G} \lambda / h$ . Otsyuda
$\Delta {g}_{1/2} = \Delta {g}_{\max } /2 = \frac{G\lambda }{2} = \frac{2G\lambda h}{({x}_{1/2} + {h}^{2} )}$

i $h^{2} =x_{1/2}^{2}$ , $h = \pm x _{ 1/2}$ , t.e. glubina zaleganiya cilindra ravna rasstoyaniyu ot tochki maksimuma $\Delta g _{ max}$ do tochki, gde $\Delta g= \Delta g _{ max } / 2$ .

Opredeliv $h$ i znaya izbytochnuyu plotnost', mozhno rasschitat'

$\lambda = \pi R ^{ 2} ( \sigma - \sigma _{ 0} ) = 0,0075 h \Delta g _{max}$

i radius cilindra:

$R = \sqrt{ \frac{0,0075h\Delta{g}_{max }}{\pi (\sigma - {\sigma }_{o} )} } .$

Znaya $R$ , mozhno poluchit' glubiny zaleganiya verhnei h_v=h-R i nizhnei h_n=h+R kromok cilindra. Netrudno vychislit' vyrazhenie i dlya $W _{ xz}$ .

Nazad| Vpered

Publikacii s klyuchevymi slovami: geofizika - Zemlya - zemnaya kora Publikacii so slovami: geofizika - Zemlya - zemnaya kora
Sm. takzhe: Protivosumerechnye luchi i festival' planet Voshod Zemli: video Udarnyi krater Manikuagan: vid iz kosmosa Zemlya i Luna: vid s drugoi storony Snezhnaya burya 1938 goda v Verhnem Michigane Polet nad nochnoi Zemlei – II Apollon-17: serp Zemli Vse publikacii na tu zhe temu >>

Mneniya chitatelei [5]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce