Astronet > Geofizicheskie metody issledovaniya zemnoi kory. Chast' 1

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Geofizicheskie metody issledovaniya zemnoi kory

1.3.4. Pryamaya i obratnaya zadacha nad vertikal'nym ustupom (sbrosom).

1. Pryamaya zadacha. Pust' vertikal'nyi ustup (sbros) prostiraetsya beskonechno vdol' osi y (ris. 1.5). Nablyudeniya proizvodyatsya vdol' osi ( x), ( y=z=0), raspolozhennoi vkrest prostiraniya sbrosa. Esli glubina do krovli z₁ i z₂ , a amplituda ustupa $h$ , to, soglasno (1.10),

$\Delta g=G(\sigma-\sigma_0) \int\limits_0^{+\infty}dx\int\limits_{-\infty}^{\infty}dy \int\limits_{z_1}^{z^2}\frac{dz}{\left[ (\bar x -x)^2+\bar y^2+\bar z^2\right]^{3/2}}.$

(1.13)

V obshem sluchae vyrazhenie integrala imeet gromozdkii vid. V chastnosti, polnaya maksimal'naya anomaliya nad ustupom (raznost' sily tyazhesti mezhdu podnyatym i opushennym krylom) opredelitsya sleduyushei formuloi:

$\Delta {g}_{\max } = 2\pi G(\sigma - {\sigma}_{o} )({z}_{2} - {z}_{1} ).$

(1.14)

Nad ustupom (x=0) anomaliya ravna polovine maksimal'noi.

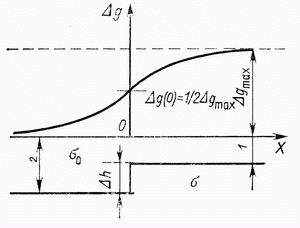Ris.1.5 Gravitacionnoe pole nad ustupom (sbrosom)

2. Obratnaya zadacha. Iz (1.14) mozhno opredelit' $h = z _{ 2} - z _{ 1} = \Delta g _{ max } /2 \pi G( \sigma - \sigma _{0} ).$

V teorii gravirazvedki dokazano, chto primernaya glubina raspolozheniya serediny vysoty ustupa $(H = ( z _{2} + z _{ 1} ) / 2)$ ravna $x_{ 1/2},$ t.e. abscisse tochki, v kotoroi $\Delta g _{ 1/2}=\Delta g _{ 0 }/2=\Delta g _{ max} / 4,$ gde $\Delta g _{ 0}$ - anomaliya nad ustupom, a $\Delta g _{ max}$ - polnaya anomaliya. Prakticheski dlya opredeleniya $H$ na krivoi $\Delta g$ nahoditsya mestopolozhenie sbrosa $( \Delta g _{ 0} ),$ i v masshtabe profilya rasschityvaetsya $x _{ 1/2}$ - rasstoyanie ot sbrosa do tochki, v kotoroi $\Delta g = \Delta g _{ 0 } / 2.$ Znaya $H$ i $h$ , legko opredelit' glubiny do pripodnyatogo $(z _{ 1} = H - h / 2)$ i opushennogo $(z _{ 2} = H + h / 2)$ kryla.

1.3.5. Graficheskoe opredelenie anomalii sily tyazhesti dvuhmernyh tel s pomosh'yu paletki Gamburceva.

1. Pryamaya zadacha. Dlya tel bolee slozhnoi formy raschet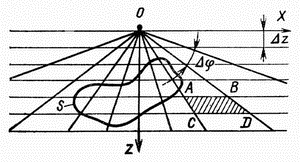 $\Delta g$ predstavlyaet bol'shie trudnosti i vypolnyaetsya libo na vychislitel'nyh mashinah, libo graficheskim putem s pomosh'yu razlichnyh paletok. Dlya vychislenii anomalii nad telami s secheniem lyuboi proizvol'noi formy i vytyanutymi vdol' osi (dvuhmernye tela) primenyaetsya paletka Gamburceva. Paletka imeet vid, pokazannyi na ris. 1.6.

Ris.1.6 Paletka Gamburceva dlya vychisleniya prityazheniya dvuhmernyh tel

Zdes' iz tochki O cherez odin i tot zhe ugol $\Delta \varphi$ provedeny radiusy, a cherez ravnye rasstoyaniya $\Delta z$ - parallel'nye linii.

Sila tyazhesti $\Delta g$ v tochke O za schet prityazheniya beskonechnoi gorizontal'noi prizmoi secheniem v vide trapecii ABCD odinakova dlya lyuboi iz takih prizm i ravna

$\Delta {g}_{p} = 2G(\sigma - \sigma )\Delta \varphi\Delta z$

(1.15)

V samom dele, vospol'zuemsya formuloi prityazheniya beskonechno dlinnym cilindrom (1.12), v kotoruyu vmesto \lambda podstavim massu elementarnoi prizmy secheniem dxdz:

$\lambda = \pi {R}^{2} (\sigma - {\sigma }_{o} )$

Prityazhenie beskonechno dlinnoi prizmoi lyubogo secheniya mozhet byt' rasschitano po formule:

$\Delta g = 2G(\sigma - {\sigma }_{o} )\int\limits\int\limits \frac{z}{{x}^{2} + {z}^{2} } dx dz .$

Zameniv $x = z\, \hbox{ctg} \, \varphi ,$ poluchim $dx = z(-1/\sin ^{ 2} \varphi ) d \varphi ,$ no $sin ^{ 2} \varphi = z ^{ 2} /(x ^{ 2} + z ^{ 2} )$ , poetomu

$\Delta g = 2G(\sigma - {\sigma }_{o} )\int\limits\int\limits dz d\varphi \approx 2G(\sigma - {\sigma }_{o} )\sum \Delta z \Delta \varphi \approx\sum\Delta {g}_{p},$

gde $\Delta g _{ p }$ - cena odnoi trapecii (cena paletki), ravnaya $\Delta {g}_{p} = 2G\Delta {\sigma }_{p}\Delta \varphi\Delta z.$

Podobrav $\Delta \sigma ,$ $\Delta \varphi$ i $\Delta z$ takimi, chtoby $\Delta g _{p}$ ravnyalos' kakomu-nibud' postoyannomu znacheniyu (naprimer, 0,1 mGal), legko rasschitat' v tochke O anomaliyu ot prizmy lyubogo secheniya, dlya chego nado podschitat' chislo trapecii, pokryvayushih sechenie issleduemogo tela (n). Anomaliya $\Delta g$ ravna n, umnozhennomu na cenu paletki i masshtabnyi koefficient

$K = \frac{\Delta {\sigma }_{p} }{\sigma - {\sigma}_{o} } \cdot\frac{{M}_{p} }{{M}_{p} },$

gde $\Delta \sigma _{ p}$ i $M _{ p}$ - izbytochnaya plotnost' i masshtab paletki, a $\sigma - \sigma _{ 0}$ i $M _{ r}$ - izbytochnaya plotnost' i masshtab razreza.

Takim obrazom, anomaliya nad dvuhmernym telom lyubogo secheniya s pomosh'yu paletki Gamburceva rasschityvaetsya po formule:

$\Delta {g} = n\Delta {g}_{p} K.$

(1.16)

2. Obratnaya zadacha. Ispol'zuya (1.16) s pomosh'yu paletki Gamburceva, mozhno vyyasnit' formu i polozhenie secheniya vozmushayushego dvuhmernogo anomalosozdayushego ob'ekta. Dlya etogo nado znat' izbytochnuyu plotnost' $\sigma - \sigma _{0}$ , ocenit' analiticheskim sposobom polozhenie ee centra i dlya neskol'kih tochek grafika $\Delta g$ postroit' vozmozhnye secheniya vozmushayushego tela. Srednee iz nih harakterizuet primernoe sechenie tela.

1.3.6. Chislennye metody resheniya pryamyh i obratnyh zadach gravirazvedki.

Dlya bolee slozhnyh form anomalosozdayushih ob'ektov pryamye zadachi gravirazvedki reshayutsya chislennymi metodami s pomosh'yu EVM. Za osnovu beretsya formula dlya gravitacionnoi anomalii, sozdannoi lyubym telom s postoyannoi ili peremennoi izbytochnoi plotnost'yu (1.10). Prakticheski chislennyi metod svoditsya k razbieniyu ob'ekta na elementarnye massy, yacheiki - naprimer, sharovoi ili kubicheskoi formy. Gravitacionnyi effekt takih mass rasschityvaetsya po formule (1.9), a zatem vedetsya ih summirovanie po vsemu ob'emu ob'ekta. Schet mozhno realizovat' s pomosh'yu EVM.

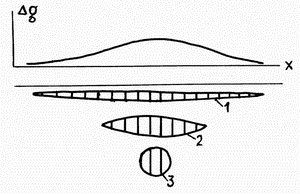Ris.1.7 K neodnoznachnosti resheniya obratnoi zadachi gravirazvedki

Obratnye zadachi reshayutsya metodom sravneniya polevoi anomalii s teoreticheski rasschitannymi, u kotoryh geometricheskie parametry i izbytochnye plotnosti postepenno izmenyayutsya do polucheniya naimen'shih rashozhdenii mezhdu krivymi. Esli pryamye zadachi, kak i vsyakie pryamye zadachi matematicheskoi fiziki, odnoznachny, to obratnye zadachi neodnoznachny (sm. 3). Na ris. 1.7 priveden shematicheskii primer togo, kak tela raznogo secheniya i glubiny zaleganiya dazhe pri postoyannoi izbytochnoi plotnosti mogut sozdat' odinakovuyu anomaliyu sily tyazhesti.

2. Apparatura, metodika i obrabotka dannyh gravirazvedki

2.1. Principy izmerenii sily tyazhesti i apparatura dlya gravirazvedki

2.1.1. Izmeryaemye v gravirazvedke parametry.

Osnovnym izmeryaemym parametrom v gravirazvedke yavlyaetsya uskorenie sily tyazhesti $g$ , kotoroe opredelyaetsya libo absolyutno, libo otnositel'no. Pri absolyutnyh izmereniyah poluchayut polnoe (nablyudennoe) znachenie uskoreniya $g _{ n}$ , pri otnositel'nyh - ego prirashenie otnositel'no nekotoroi ishodnoi tochki $\Delta g _{ n} .$

Metody izmereniya uskoreniya sily tyazhesti i ego prirasheniya delyatsya na dinamicheskie i staticheskie. Pod dinamicheskimi ponimayutsya takie metody, v kotoryh nablyudaetsya dvizhenie tela pod deistviem sily tyazhesti (kachanie mayatnika, svobodnoe padenie tel i dr.) V etom sluchae g opredelyaetsya cherez parametry dvizheniya tela i parametry ustanovki. V staticheskih metodah deistvie sily tyazhesti kompensi\-ruetsya (naprimer, siloi uprugosti pruzhiny), a g opredelyaetsya po izmeneniyu staticheskogo polozheniya ravnovesiya tela.

Rezhe v gravirazvedke izmeryayutsya vtorye proizvodnye gravitaci\-onnogo potenciala $W _{ xy} , W _{xz} , W _{ yz} , ( W _{ yy} -W _{ xx} ).$

2.1.2. Dinamicheskie metody.

a). Naibolee ispol'zuemyi dinamicheskii metod - mayatnikovyi. Dlya abstraktnogo ob'ekta - matematicheskogo mayatnika - period kolebanii

$T = \pi \sqrt{l/g} (1 + \frac{1}{4}{\sin }^{2} \alpha /2 + \frac{9}{64} {\sin }^{4} \alpha /2),$

gde $l$ - dlina mayatnika, $g$ - uskorenie sily tyazhesti, $\alpha$ - maksimal'noe znachenie ugla otkloneniya mayatnika ot vertikali. Eta formula ostaetsya spravedlivoi i dlya real'nogo ob'ekta - fizicheskogo mayatnika, esli v kachestve $l$ vzyat' tak nazyvaemuyu privedennuyu dlinu $l = Jma,$ gde $J$ - moment inercii mayatnika, $m$ - massa, $a$ - rasstoyanie ot centra tyazhesti do osi vrasheniya. Pri malyh $\alpha$ formula dlya perioda prinimaet vid $T \approx \pi \sqrt{l/g} .$ Tochnost' opredeleniya perioda vozrastaet pri uvelichenii vremeni nablyudeniya za kolebaniyami mayatnika. Dlya absolyutnyh izmerenii uskoreniya sily tyazhesti neobhodimo izmeryat' dlinu mayatnika. Znaya $g _{ 0}$ i ${T}_{o} = \pi \sqrt{l/g}$ na ishodnoi tochke, a takzhe ${T}_{i} = \pi \sqrt{l/{g}_{i} }$ na i-toi tochke, mozhno vypolnit' otnositel'nye izmereniya v dvuh tochkah: po formule $g _{ i} = g _{ 0} ( T _{0} - T _{ i} ) ^{ 2} ,$ t.e. v otnositel'nyh izmereniyah dlinu opredelyat' ne nado.

Hotya mayatnikovye pribory i podverzheny vozdeistviyu temperatury, vlazhnosti i drugih faktorov, oni harakterizuyutsya ochen' medlennym i plavnym spolzaniem nul'-punkta (izmeneniem zavisimosti pokazanii v odnoi i toi zhe tochke ot vremeni, vyzvannym stareniem sistemy).

Pri izmereniyah mayatnikovymi priborami v dvizhenii, naprimer, pri morskih s'emkah, vliyanie kachki mozhno sushestvenno snizit', esli primenyat' neskol'ko mayatnikov, zakreplennyh na odnom osnovanii. V etom sluchae ih kolebaniya obychno svodyat k kolebaniyam odnogo empiricheskogo mayatnika, ispol'zuya slozhnyi matematicheskii apparat.

Pogreshnost' absolyutnyh izmerenii uskoreniya sily tyazhesti mayatnikovymi priborami mozhno dovesti do 1 - 3 mGal, a otnositel'nyh - pri nazemnyh issledovaniyah - do 0.1 mGal, pri morskih s'emkah - do 5 - 10 mGal.

b). Opredelenie absolyutnogo znacheniya uskoreniya sily tyazhesti mozhno provodit' metodom svobodnogo padeniya, kogda izmeryaetsya vremya svobodnogo padeniya tela i rasstoyanie, proidennoe telom. Izmereniya otlichayutsya bol'shoi trudoemkost'yu i vypolnyayutsya na observatoriyah, gde tochnost' v opredelenii $g$ mozhno dovesti do 0,01 mGal.

v). V nastoyashee vremya izvestny metody absolyutnyh i otnositel'nyh izmerenii sily tyazhesti, osnovannye na izuchenii kolebanii strun. V nih izmeryaetsya chastota kolebanii struny, ee dlina i massa. V rezul'tate mozhno rasschitat' $g$ ili $\Delta g$ .

Nazad| Vpered

Publikacii s klyuchevymi slovami: geofizika - Zemlya - zemnaya kora Publikacii so slovami: geofizika - Zemlya - zemnaya kora
Sm. takzhe: Protivosumerechnye luchi i festival' planet Voshod Zemli: video Udarnyi krater Manikuagan: vid iz kosmosa Zemlya i Luna: vid s drugoi storony Snezhnaya burya 1938 goda v Verhnem Michigane Polet nad nochnoi Zemlei – II Apollon-17: serp Zemli Vse publikacii na tu zhe temu >>

Mneniya chitatelei [5]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce