Astronet > Geofizicheskie metody issledovaniya zemnoi kory. Chast' 2

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Geofizicheskie metody issledovaniya zemnoi kory

5.3.8. Oppedelenie deformacionno-ppochnostnyh svoistv gornyh popod po dannym seismorazvedki i seismoakusticheskih issledovanii.

Po skopostyam ppodol'nyh (zhelatel'no i popepechnyh) uppugih voln, poluchaemyh v rezul'tate interpretacii dannyh seismorazvedki MPV, MOV i seismoakusticheskih issledovanii skvazhin, oppedelyayutsya dinamicheskie defopmacionno-ppochnostnye svoistva gornyh popod v massive v estestvennyh usloviyah zaleganiya, po kotopym, v svoyu ochered', ocenivayutsya staticheskie deformacionno-prochnostnye svoistva [Kompleksnye inzhenerno-geofizicheskie issledovaniya pri stroitel'stve gidrotehnicheskih sooruzhenii, 1990; Savich A.I., Yashenko Z.G., 1979].

Dinamicheskii koefficient popepechnyh defopmacii (koefficient Puassona $\nu _{ g}$ ) zavisit ot otnosheniya $V _{ s} / V _{ p}$ , kotopoe menyaetsya ot 0,2 do 0,7. Ego rasschityvayut po formule $\nu = ( V _{ p} ^{ 2} - 2 V _{ s} ^{ 2} ) / 2( V _{ p} - V _{ s} ^{ 2} )$ ili opredelyayut po pravoi shkale nomogrammy na ris. 5.9. S pomosh'yu etoi zhe nomogrammy opredelyaetsya dinamicheskii modul' Yunga $E _{ g} = 2 V _{ s} ^{ 2} \sigma (1 + \nu )$ ( $E _{ g}$ - v MPa, $V _{ s}$ - v km/s, $\sigma$ - v g/sm³). Zametim, chto vse uppugie moduli izmepyayutsya v paskalyah (Pa), gigapaskalyah (1 GPa = 10⁹ Pa), megapaskalyah (1 MPa = 10⁶ Pa) ili v n'yutonah na 1 kv. m (1 N/m² = 10 Pa = 10^-5 kg/sm² ).

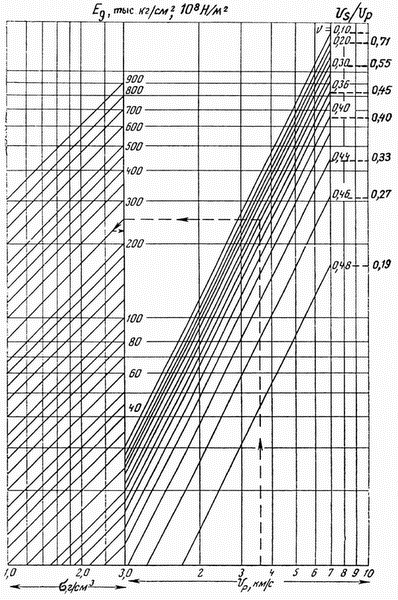Ris. 5.9. Nomogramma V.N.Nikitina dlya vychisleniya dinamicheskogo modulya uprugosti ( $E _{ g}$ ) po $V _{ r} , \sigma , \nu$ [Savich A.I., Yashenko Z.G., 1979]

Nomogramma na ris. 5.9 pozvolyaet opredelit' dostatochno tochno parametry $\nu _{ g}$ i $E _{ g}$ (pogreshnosti ne prevyshayut 20%) dlya sploshnyh odnorodnyh i izotropnyh uprugih sred, k kotorym mozhno otnesti skal'nye porody. Dlya diskretnyh neodnorodnyh (poluskal'nye i ryhlye osadochnye) i osobenno anizotropnyh (slancy, gliny) geologicheskih sred poluchaemye s pomosh'yu etoi nomogrammy parametry $\nu _{ g}$ i $E _{ g}$ yavlyayutsya effektivnymi, t.e. harakterizuyut usrednennye uprugie svoistva. S dostatochnoi tochnost'yu oni mogut ispol'zovat'sya dlya polucheniya lish' otnositel'nyh znachenii $\Delta \nu _{ g} , \Delta E _{ g}$ , kotorymi opredelyaetsya uprugaya neodnorodnost' sredy. Absolyutnye zhe velichiny etih modulei mozhno poluchit', ustanoviv korrelyacionnye svyazi mezhdu geologo-geofizicheskimi svoistvami izuchaemogo raiona. V celom dlya pazlichnyh popod $\nu _{ g}$ menyaetsya ot 0,1 do 0,5, a $E _{ g}$ - ot edinic do soten 10² MPa (ot dolei edinic do desyatkov GPa).

Poskol'ku pri inzhenerno-geologicheskih ispytaniyah poluchayutsya staticheskie, a v MPV i MOV dinamicheskie moduli uprugosti, to mezhdu nimi pytayutsya ustanovit' korrelyacionnye svyazi. Dlya skal'nyh i merzlyh porod takie svyazi dovol'no ustoichivy. Tak, dlya skal'nyh porod V.N.Nikitinym pekomenduetsya zavisimost' $E _{ c} = 1,03 E _{ g} - 0,9$ ( $E$ - v GPa). E _{ c} nazyvaetsya privedennym modulem uprugosti i shiroko ispol'zuetsya pri izuchenii skal'nyh massivov gornyh porod. Pogreshnosti pri raschetah $E _{ c}$ dostigayut 40%. Dlya poluskal'nyh i ryhlyh porod eti svyazi v kazhdom raione ustanavlivayutsya putem korrelyacii mezhdu geologo-geofizicheskimi parametrami.

Modul' obshei deformacii ( $E _{ def}$ ), harakterizuyushii polnye uprugie deformacii v massive pri znachitel'nyh dlitel'nyh nagruzkah odnogo znaka, slozhnym obrazom zavisit ot $E _{ s}$ i $E _{ g}$ , a analiticheskie svyazi mezhdu nimi ne ustanovleny. Obobshennye mnogimi avtorami eksperimental'nye zavisimosti $E _{ def}$ ot $E _{ g}$ predstavleny na ris. 5.10.

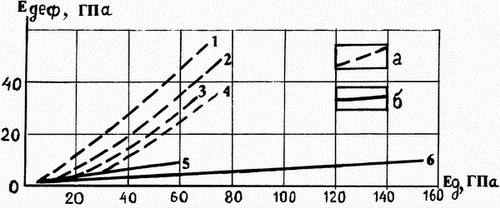Ris. 5.10. Grafiki zavisimosti obshego modulya deformacii ( $E _{ def}$ ) ot dinamicheskogo modulya uprugosti ( $E _{ g}$ ) dlya raznyh porod: 1 i 3 - vozdushno-suhih i vodonasyshennyh magmaticheskih i metamorficheskih, 2, 5 i 4, 6 - vozdushno-suhih i vodonasyshennyh osadochnyh pri ispytaniyah na obrazcah ( a) i naturnyh nablyudeniyah ( b) [Savich A.I., Yashenko Z.G., 1979]

Modul' obshei deformacii skal'nyh porod mozhet byt' ocenen libo s pomosh'yu ris. 5.10, libo vychislen po formule V.I.Bondareva: $E _{ def} = (0,093 E _{ g} + 0,4)$ MPa. Dlya peschano-glinistyh porod ego mozhno opredelit' s pomosh'yu grafikov, predstavlennyh na ris. 5.11, esli izvestny skorosti rasprostraneniya prodol'nyh voln. Maksimal'nye znacheniya $E _{ def}$ u massivnyh skal'nyh gornyh popod (10000-50000) MPa = (10-50) GPa, a u poluskal'nyh - v 100 paz men'she.

Ris. 5.11. Grafiki zavisimosti modulya obshei deformacii ( $E _{ def}$ ) ot skorosti rasprostraneniya prodol'nyh uprugih voln $V _{ r}$ dlya peschano-glinistyh porod raznoi plotnosti ( $\sigma$ ) [Savich A.I., Yashenko Z.G., 1979]

Sredi prochnostnyh svoistv gornyh porod chasto ispol'zuetsya predel prochnosti na szhatie ( $\sigma _{ szh}$ ), ravnyi napryazheniyu odnoosnogo szhatiya obrazca, pri kotorom on razrushaetsya. Predel prochnosti harakterizuet krepost' porod s tochki zreniya perenosimyh nagruzok. Formula dlya rascheta $\sigma _{ szh}$ obrazcov nevodonasyshennyh skal'nyh porod imeet vid $\sigma _{ szh} = [ V _{ p} ^{ 2} \sigma _{ g} (1 - 2 \nu _{ g} )] / [(1 - \nu _{ g} ) \cdot C]$ ( $\sigma _{ szh}$ - v Pa, $V _{ p}$ - v m/s, $\sigma _{ g}$ - v kg/m³), gde koefficient $S$ ustanavlivaetsya putem polucheniya korrelyacionnyh svyazei pri eksperimental'nyh geologo-geofizicheskih nablyudeniyah. On priblizitel'no raven: 240 (dlya izvestnyakov), 180 (dlya metamorficheskih i drevnih (doyurskih) effuzivnyh porod), 120 (dlya drevnih intruzivnyh porod), 60 (dlya molodyh (posleyurskih) skal'nyh porod). Velichinu $\sigma _{ szh}$ (v MPa) cherez $V _{ p}$ (v km/s) dlya skal'nyh porod mozhno opredelit' s pomosh'yu grafikov, predstavlennyh na ris. 5.12, a dlya glin - po formule N.N.Goryainova $\sigma _{ szh} = 0,7 V _{ p} ^{ 2} - 0,07$ . Dlya ryhlyh osadochnyh porod $\sigma _{ szh}$ svyazan s $V _{ p}$ i $V _{ s}$ zavisimost'yu $\sigma _{ szh} \gg V _{ p} ^{ 2} / \nu ^{ 4} \gg SV _{ s} ^{ 2} / \nu ^{ 2}$ , gde $\sigma _{ szh}$ - v MPa, $V$ - v km/s, $\nu$ - koefficient Puassona, $S$ - koefficient, kotoryi pri otnositel'nyh izmereniyah mozhno prinyat' za 1, a pri absolyutnyh ego sleduet opredelit' s pomosh'yu sovmestnyh geologo-geofizicheskih rabot. V celom naibol'shie znacheniya $\sigma _{ szh}$ (200-300 MPa) nablyudayutsya v massivnyh magmaticheskih popodah, ppimepno v 2 paza men'shie $\sigma _{ czh}$ - u skal'nyh osadochnyh popod i v 100-200 raz men'shie - u sil'no tpeshinovatyh poluskal'nyh popod.

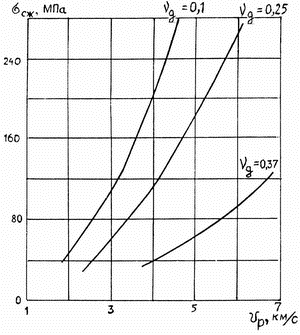Ris. 5.12. Teoreticheskie grafiki zavisimosti predela prochnosti porod na szhatie ( $\sigma _{ szh}$ ) ot skorosti prodol'nyh voln ( $V _{ p}$ ) dlya raznyh znachenii $\nu _{ g}$ skal'nyh porod [Savich A.I., Yashenko Z.G., 1979]

V celom s pomosh'yu dostatochno prostogo i bystrogo geofizicheskogo metoda (MPV) poluchayutsya kolichestvennye parametry dlya postroeniya obobshennyh geomehanicheskih modelei geologicheskoi sredy, neobhodimyh pri proektirovanii sooruzhenii. Absolyutnye znacheniya fiziko-mehanicheskih svoistv opredelyayutsya s pogreshnostyami do 20%, a deformacionno-prochnostnyh - popyadka 50%. Odnako otnositel'nye izmeneniya teh ili inyh parametrov vdol' profilei ili v predelah ploshadei provedeniya MPV, t.e. ih prostranstvennaya izmenchivost', oppedelyayutsya znachitel'no tochnee. V rezul'tate osushestvlyaetsya kartirovanie geologicheskoi sredy, t.e. raschlenenie ee na neodnorodnye zonal'no-blokovye uchastki raznyh razmerov. Po razlichiyam seismicheskih i geomehanicheskih svoistv na izuchaemoi ploshadi eti uchastki tol'ko po geofizicheskim dannym mozhno razdelit' na otnositel'no ustoichivye s tochki zreniya stroitel'stva, gde $V _{ r} , V _{ s} , \sigma , E _{ g} , E _{ s} , E _{ def} , \sigma _{ szh}$ dostigayut maksimumov, i neustoichivye, gde eti parametry men'she maksimal'nyh v 5-10 raz.

5.4. Merzlotno-glyaciologicheskaya geofizika

5.4.1. Stroenie merzlyh porod i zadachi ih izucheniya.

Geofizicheskie metody davno primenyayut pri merzlotnyh issledovaniyah, t.e. pri izuchenii takih slozhnyh ob'ektov i yavlenii prirodnoi geologicheskoi sredy, kakimi yavlyayutsya mnogoletnemerzlye porody moshnost'yu ot edinic do soten metrov. Oni otlichayutsya otricatel'nymi temperaturami pri polozhitel'nyh temperaturah podstilayushih porod. Perekryvayushii mnogoletnemerzlye porody deyatel'nyi sloi moshnost'yu 0,3-3 m harakterizuetsya polozhitel'nymi temperaturami v techenie men'shei chasti goda (letom) i otricatel'nymi temperaturami na protyazhenii ostal'noi chasti goda.

Fizicheskie svoistva l'dov i mnogoletnemerzlyh gornyh porod opredelyayutsya prezhde vsego ih temperaturoi, hotya i drugie prirodnye faktory (litologiya, struktura, tekstura, poristost', vodonasyshennost', mineralizaciya podzemnyh vod) okazyvayut na nih sushestvennoe vliyanie. Geologo-geofizicheskie razrezy v raionah rasprostraneniya mnogoletnemerzlyh porod harakterizuyutsya bol'shoi izmenchivost'yu v prostranstve i vo vremeni.

Geofizicheskie metody mozhno primenyat' dlya resheniya sleduyushih treh grupp zadach:

kartirovaniya merzlyh i talyh otlozhenii (vyyavlenie litologicheskih kontaktov, tektonicheskih narushenii, zon treshinovatosti, uchastkov skvoznyh i neskvoznyh talikov, podzemnyh l'dov, obvodnennyh zon);
raschleneniya merzlyh i talyh gornyh porod po glubine (opredelenie krovli i podoshvy mnogoletnemerzlyh porod, izuchenie rasprostraneniya na glubine merzlyh i talyh porod, skvoznyh i neskvoznyh talikov, t.e. vyyasnenie stroeniya mnogoletnemerzlyh porod v plane i po glubine, poiski i razvedka mezhmerzlotnyh i podmerzlotnyh podzemnyh vod);
izucheniya merzlotnyh processov i yavlenii, v tom chisle dinamiki sezonnogo promerzaniya i ottaivaniya, processov naledeobrazovaniya, pucheniya, termokarsta, morozoboinogo rastreskivaniya i dr.

Nazad| Vpered

Publikacii s klyuchevymi slovami: geofizika - Zemlya - zemnaya kora Publikacii so slovami: geofizika - Zemlya - zemnaya kora
Sm. takzhe: Zamerzshie puzyri metana v ozere Baikal Zemlya iz mezhplanetnogo prostranstva Zahod Zemli s "Oriona" Protivosumerechnye luchi i festival' planet Voshod Zemli: video Udarnyi krater Manikuagan: vid iz kosmosa Zemlya i Luna: vid s drugoi storony Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce