Astronet > Obychnye i neobychnye fazovye perehody

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Obsuzhdaetsya klassifikaciya fazovyh perehodov i povedenie sistem, sovershayushih fazovye perehody pervogo i vtorogo roda. Rassmotreno otryvanie adsorbirovannoi polimernoi cepi ot ploskosti pod deistviem postoyannoi vneshnei sily. Pokazano, chto v etom sluchae imeet mesto neobychnyi fazovyi perehod, imeyushii cherty perehodov pervogo i vtorogo roda odnovremenno.

Model' "lipkoi lenty"

Polimernye cepi v rastvore predstavlyayut soboi dlinnye niti, haoticheski svernutye v prostranstve i postoyanno menyayushie svoyu formu i razmery pod deistviem teplovyh besporyadochnyh udarov molekul rastvoritelya. Poluchit' predstavlenie o svoistvah polimernyh cepei v rastvore mozhno, prochitav populyarnye knigi [Grosberg A.Yu., Hohlov A.R.,1989],[Elias G.G.,1990]. Rassmotrim polimernuyu molekulu, plavayushuyu v rastvore vblizi nekotoroi ploskoi poverhnosti. Zakrepim odin konec polimernoi cepi na ploskosti, a vtoroi ostavim svobodnym. Togda polimernaya cep' budet napominat' dlinnuyu vodorosl', rastushuyu na dne pruda (ris. 5). Esli dno pruda lipkoe, to takaya vodorosl' skoro okazhetsya skreplennoi s poverhnost'yu dna razlichnymi svoimi uchastkami. Analogichnym obrazom vedet sebya polimernaya cep' vblizi adsorbiruyushei (lipkoi) poverhnosti. Pri bol'shoi energii adsorbcii pochti vse uchastki cepi budut lezhat' na poverhnosti. V etom sostoyanii polimernuyu cep' mozhno predstavit' kak dlinnuyu lipkuyu lentu (ris. 5).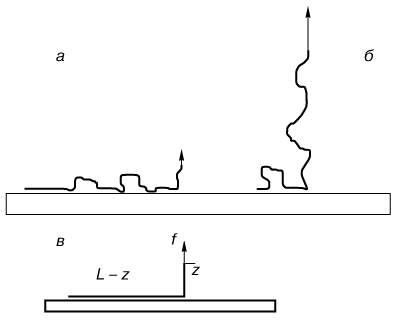

Izobrazhenie polimernoi cepi, adsorbirovannoi na ploskosti pri nebol'shoi otryvayushei sile (a) i pochti polnost'yu otorvannoi ot ploskosti pri bol'shoi sile (b). Model'

Ris. 5. Izobrazhenie polimernoi cepi, adsorbirovannoi na ploskosti pri nebol'shoi otryvayushei sile (a) i pochti polnost'yu otorvannoi ot ploskosti pri bol'shoi sile (b). Model' "lipkoi lenty" (v).

Prilozhim teper' k svobodnomu koncu polimernoi cepi postoyannuyu silu f, napravlennuyu perpendikulyarno ploskosti i otryvayushuyu cep' ot ploskosti. Konturnuyu dlinu makromolekuly oboznachim cherez L, a cherez q oboznachim silu adsorbcii, s kotoroi uderzhivaetsya na ploskosti uchastok cepi edinichnoi dliny. Esli svobodnyi konec cepi nahoditsya na vysote z, to potencial'naya energiya otorvannoi chasti ravna fz. Ostal'naya chast' cepi dlinoi $L-z$ adsorbirovana na ploskosti, imeya energiyu $q(L-z)$ . Pri otryvanii polimernoi cepi zatrachivaetsya rabota po preodoleniyu energii adsorbcii, no vyigryvaetsya potencial'naya energiya, svyazannaya s pod'emom konca cepi nad ploskost'yu. Ochevidno, otryvanie proizoidet pri $f=q$ , kogda otryvayushaya sila sravnyaetsya s adsorbcionnoi siloi. Veroyatnost' nahozhdeniya svobodnogo konca cepi na vysote z imeet vid

$P(z)\sim \exp{[fz+q(l-z)]}\sim \exp (tz/l).$

(2)

gde $t = (f - q)L$ .
Rassmotrim stepen' vytyanutosti konca polimernoi cepi nad ploskost'yu $S=z/L$ . Na risunke 6 pokazana zavisimost' srednei stepeni vytyanutosti ot velichiny $f-q$ . Budem schitat', chto lipkost' poverhnosti, to est' velichina q, postoyanna. Kak vidno iz risunka 6, po mere vozrastaniya otryvayushei sily vysota konca polimernoi molekuly uvelichivaetsya. Chem dlinnee makromolekula, tem bolee rezko proishodit perehod cepi iz adsorbirovannogo v otorvannoe sostoyanie. V predele beskonechno dlinnoi polimernoi cepi velichina <S>, a sledovatel'no, i energiya makromolekuly izmenyatsya skachkom pri $f = q$ . Kak uzhe govorilos' v razdele Klassifikaciya fazovyh perehodov, takoe skachkoobraznoe izmenenie energii sistemy yavlyaetsya harakternym priznakom fazovyh perehodov pervogo roda.

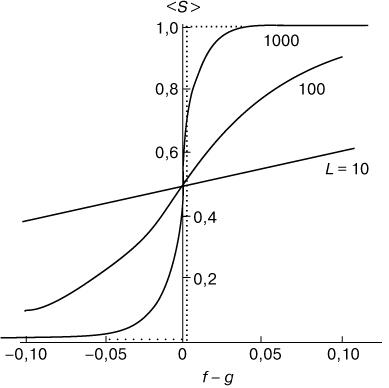Zavisimost' stepeni vytyanutosti polimernyh cepei razlichnoi dliny ot raznosti otryvayushei sily i sily adsorbcii v modeli

Ris. 6. Zavisimost' stepeni vytyanutosti <S> s polimernyh cepei razlichnoi dliny L ot raznosti $f - g$ otryvayushei sily i sily adsorbcii v modeli "lipkoi lenty". Povedenie asimptoticheski dlinnoi cepi pokazano punktirom.

Posmotrim, kak proyavlyaetsya fazovyi perehod v polimernoi cepi, soderzhashei nebol'shoe chislo zven'ev, to est' v "maloi sisteme". Zafiksiruem velichinu $f - q$ , to est' udalennost' ot tochki fazovogo perehoda, i rassmotrim povedenie parametra <S> v zavisimosti ot dliny makromolekuly (ris. 7). Umen'sheniyu $L-1$ otvechaet perehod ot maloi sistemy (korotkoi cepi) k bol'shoi sisteme (dlinnoi cepi). Beskonechno dlinnaya cep' pri $f - q > 0$ nahoditsya v otorvannom sostoyanii, imeya maksimal'nuyu vytyanutost', ravnuyu edinice. Pri $f - q < 0$ dlinnaya polimernaya cep' vylozhena na ploskosti i imeet nulevuyu vytyanutost'. V to zhe vremya vytyanutost' korotkih cepei vblizi tochki fazovogo perehoda - pri $f - q$ , blizkih k nulyu, - vsegda blizka k 1/2 nezavisimo ot znaka $f - q$ . Mozhno skazat', chto, nahodyas' vblizi tochki perehoda, korotkaya polimernaya cep' "ne znaet", k kakoi faze ona prinadlezhit, i v oblasti perehoda oba sostoyaniya dlya nee odinakovo veroyatny.

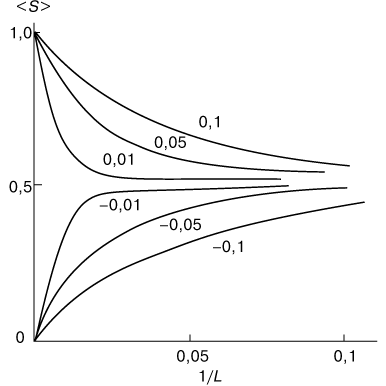Zavisimost' stepeni vytyanutosti makromolekuly ot ee obratnoi dliny pri razlichnom udalenii ot tochki fazovogo perehoda v modeli

Ris. 7. Zavisimost' stepeni vytyanutosti makromolekuly <S> ot ee obratnoi dliny 1/L pri razlichnom udalenii ot tochki fazovogo perehoda $f = g$ v modeli "lipkoi lenty".

Estestvenno vvesti harakternuyu dlinu makromolekuly L^*, pri dostizhenii kotoroi cep' mozhno nachinat' schitat' "dlinnoi", opredeliv L^* sootnosheniem

$L^*\approx ||f-q||^-1$ .

(3)

Takaya harakternaya dlina v deistvitel'nosti predstavlyaet soboi nekotoruyu oblast', a ne kakoe-to tochnoe znachenie. V dlinnyh polimernyh molekulah s $L\gg L^*$ (v "bol'shih" sistemah) svoistva rezko menyayutsya s izmeneniem $f - g$ v okrestnosti perehoda. Stepen' vytyanutosti i energiya takih molekul proporcional'ny 1/L, i ih naklon opredelyaetsya znakom velichiny $f - q$ . S drugoi storony, svoistva korotkih cepei, to est' "malyh" sistem, slabo zavisyat ot upravlyayushego parametra $f - q$ . Vdali ot tochki fazovogo perehoda velichina L^* mala i dazhe ne ochen' dlinnuyu polimernuyu cep' mozhno rassmatrivat' kak termodinamicheski obychnuyu, "bol'shuyu" sistemu. Vblizi tochki perehoda L^* stanovitsya ochen' bol'shoi velichinoi i tol'ko ochen' dlinnaya polimernaya cep' budet obladat' harakteristikami opredelennoi fazy, v to vremya kak menee dlinnye molekuly budut predstavlyat' soboi "malye" sistemy. V nizkomolekulyarnyh sistemah chislo elementov obychno stol' veliko (poryadka chisla Avogadro), chto eti sistemy vsegda mozhno schitat' asimptoticheski bol'shimi. Vliyanie razmerov sistemy na ee svoistva v okrestnostyah fazovogo perehoda rassmatrivayut tol'ko pri modelirovanii takih sistem na komp'yuterah. Pri etom, chtoby poluchit' predel'nye asimptoticheskie znacheniya velichin, provodyat ekstrapolyaciyu rezul'tatov po 1/L. Kak vidno iz risunka 7, takie ekstrapolyacii imeyut smysl tol'ko dlya "bol'shih" sistem. Pol'zuyas' formuloi (2), mozhno vychislit' lyubye harakteristiki otryvaemoi cepi i, v chastnosti, ee teploemkost'. Okazyvaetsya, chto dlya beskonechno dlinnoi adsorbirovannoi cepi, otryvaemoi ot ploskosti postoyannoi siloi, imeetsya rezkii vsplesk teploemkosti v tochke $f = q$ , chto takzhe harakterno dlya fazovyh perehodov pervogo roda.

Otsutstvie bimodal'nosti u funkcii raspredeleniya

Povedenie energii i teploemkosti pri otryvanii polimernoi cepi ot lipkoi ploskosti postoyannoi siloi vpolne soglasuetsya s obsheprinyatymi predstavleniyami o fazovom perehode pervogo roda v etoi sisteme. Odnako, kak my uvidim nizhe, v rassmatrivaemoi sisteme imeetsya ryad chert, svoistvennyh fazovym perehodam vtorogo roda. Obratimsya k raspredeleniyu svobodnogo konca cepi po vysote - formula (2). Poskol'ku potencial'naya energiya proporcional'na vysote konca $S = z / L$ , to funkciya raspredeleniya po energii $P(S)\sim\exp(tS)$ imeet tot zhe vid, chto i raspredelenie po vysote, i ne yavlyaetsya bimodal'noi ni pri kakih znacheniyah vneshnih parametrov; ona vsegda ili eksponencial'no ubyvaet, ili eksponencial'no vozrastaet, a v samoi tochke perehoda predstavlyaet soboi konstantu. Sootvetstvenno pri otryvanii "lipkoi lenty" vsegda sushestvuet tol'ko odno ravnovesnoe znachenie vysoty konca, a sledovatel'no, i srednei energii sistemy. Estestvenno, chto pri etom nikakih metastabil'nyh sostoyanii sistemy net v principe, chto harakterno dlya fazovyh perehodov vtorogo roda. My rassmatrivali otryvanie adsorbirovannoi makromolekuly, ispol'zuya prostuyu model' "lipkoi lenty", odnako okazyvaetsya, chto i gorazdo bolee detal'noe opisanie privodit k tem zhe rezul'tatam. Interesno ponyat', pochemu otryvaemaya ot poverhnosti polimernaya cep' sovershaet neobychnyi fazovyi perehod, otlichnyi ot fazovyh perehodov v nizkomolekulyarnyh sistemah. Dlya etogo vozvratimsya k nachalu stat'i i vspomnim, chto govorilos' o granice razdela mezhdu fazami i o poyavlenii zarodyshei novoi fazy pri perehodah pervogo roda. Pri poyavlenii novoi fazy nado otgranichit' ee ot drugoi fazy. Sozdanie takoi granicy energeticheski nevygodno i trebuet preodoleniya nekotorogo potencial'nogo bar'era. Imenno iz-za nalichiya takogo bar'era stanovyatsya vozmozhnymi peregretye i pereohlazhdennye metastabil'nye sostoyaniya zhidkosti i para. V polimernoi cepi est' dva razlichnyh sostoyaniya - adsorbirovannoe i otorvannoe. Granicei mezhdu etimi sostoyaniyami (fazami) yavlyaetsya vsego odno zveno. Fakticheski v etoi sisteme net poter' na sozdanie granicy, a znachit, net i bar'era, zatrudnyayushego poyavlenie novoi fazy. Raz net bar'era, to net i metastabil'nyh sostoyanii, net bimodal'nosti funkcii raspredeleniya.

Zaklyuchenie

Itak, pri otryvanii adsorbirovannoi polimernoi molekuly imeet mesto neobychnyi fazovyi perehod. Etot perehod, s odnoi storony, obladaet chertami, harakternymi dlya fazovyh perehodov pervogo roda: skachok energii, vsplesk fluktuacii i vydelenie skrytoi teploty. S drugoi storony, v povedenii rassmatrivaemoi sistemy proyavlyayutsya cherty fazovogo perehoda vtorogo roda: polnoe otsutstvie metastabil'nyh sostoyanii i otsutstvie bimodal'nosti u funkcii raspredeleniya po energii. Neobychnost' fazovogo perehoda pri otryvanii adsorbirovannoi polimernoi molekuly svyazana s neobychnost'yu granicy, sushestvuyushei mezhdu ee sostoyaniyami (fazami). Eta granica chetko opredelena i naglyadna, no stol' uzka, chto energeticheskie poteri na ee sozdanie prenebrezhimo maly. Zamechatel'nym svoistvom rassmatrivaemoi polimernoi sistemy yavlyaetsya vozmozhnost' poluchit' strogoe analiticheskoe opisanie obeih faz v ramkah edinogo rassmotreniya s pozicii statisticheskoi fiziki. Bolee togo, okazyvaetsya vozmozhnym prosledit' analiticheski, kak po mere uvelicheniya chisla chastic v sisteme formiruyutsya skachki, harakternye dlya fazovyh perehodov pervogo roda. Dlya klassicheskih nizkomolekulyarnyh sistem, sovershayushih fazovye perehody pervogo roda, edinoobraznoe opisanie obeih faz dostigaetsya tol'ko v rezul'tate chislennyh raschetov na komp'yuterah, a issledovanie effektov, svyazannyh s konechnost'yu sistemy, predstavlyaet slozhneishuyu zadachu i trebuet izoshrennyh metodov. Reshenie zadachi ob otryvanii adsorbiruyusheisya makromolekuly zakladyvaet osnovu dlya postroeniya teorii adgezionnoi prochnosti polimerov na granice razdela faz.

Literatura

Shteinberg A.S. Reportazh iz mira splavov. Bibliotechka "Kvant". M.: Nauka, 1989.
Vol'kenshtein M.V. Fizika i biologiya. M.: Nauka, 1980.
Etkins P. Fizicheskaya himiya. T. 1. Gl. 7. M.: Mir. 1980.
Landau L.D., Lifshic E.M. Statisticheskaya fizika. Chast' 1. M.: Nauka, 1976.
Grosberg A.Yu., Hohlov A.R. Fizika v mire polimerov. Bibliotechka "Kvant". M.: Nauka, 1989.
Elias G.G. Megamolekuly. L.: Himiya, 1990.

Nazad

Publikacii s klyuchevymi slovami: fazovye perehod vtorogo roda - fazovye perehod pervogo roda - fazovyi perehod Publikacii so slovami: fazovye perehod vtorogo roda - fazovye perehod pervogo roda - fazovyi perehod
Sm. takzhe: Dal'nii i blizhnii poryadok Vvedenie v fiziku otkrytyh sistem Obychnye i neobychnye fazovye perehody Agregatnye sostoyaniya

Mnenie chitatelya [1]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce