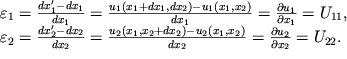Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Lekciya 1

Deformacii tverdogo tela. Ponyatie o tenzore deformacii. Absolyutno uprugoe telo i ego deformacii. Uprugie napryazheniya. Moduli Yunga, sdviga i koefficient Puassona. Deformacii pri izgibe i kruchenii, ustoichivost' tel pri deformaciyah. Energiya uprugih deformacii. V lekciyah po mehanike tverdogo tela my predpolagali, chto pod deistviem prilozhennyh sil v tele, hotya i proishodyat deformacii, tem ne menee my ne prinimali ih v raschet dlya opisaniya dvizheniya etogo tela kak celogo. Vo mnogih vazhnyh sluchayah uchet deformacii yavlyaetsya opredelyayushim, naprimer, kogda rech' idet o celoi oblasti fiziki - o mehanike sploshnoi sredy ili o raschete prochnosti mnogochislennyh konstrukcii i detalei mashin i mehanizmov, baziruyushemsya na otdel'noi inzhenernoi nauke, nazyvaemoi soprotivlenie materialov i t.d. Vnachale my rassmotrim povedenie tverdyh tel, kotorye deformiruyutsya pod deistviem prilozhennyh sil. Nado otmetit', chto osnovnoe polozhenie mehaniki deformiruemyh tverdyh tel, rassmatrivaemyh kak sploshnye sredy, byli razrabotany v nachale XIX v. I sostavlyayut osnovu sovremennoi teorii uprugosti. Opyt pokazyvaet, chto pod deistviem prilozhennyh sil tela v toi ili inoi stepeni menyayut svoyu formu i ob'em, chto na mikroskopicheskom urovne oznachaet otnositel'noe smeshenie atomov, sostavlyayushih telo. Dlya udobstva opisaniya deformacii myslenno razob'em telo na fizicheski malye ob'emy (inogda ih budem nazyvat' chasticy), soderzhashie, odnako, bol'shoe chislo atomov. V otsutstvie deformacii atomy nahodyatsya v sostoyanii teplovogo ravnovesiya, a vse malye ob'emy - v mehanicheskom ravnovesii. Togda summa sil, deistvuyushih na vydelennyi ob'em so storony primykayushih k nemu drugih ob'emov budet ravna nulyu. Smena raspolozheniya atomov pri deformaciyah privodit k tomu, chto v tele voznikayut vnutrennie sily, ili vnutrennee napryazhenie, stremyashiesya vernut' telo v sostoyanie ravnovesiya. Vazhno otmetit', chto vnutrennie sily, kak sily molekulyarnogo vzaimodeistviya, yavlyayutsya korotkodeistvuyushimi. Tol'ko sosednie atomy ili molekuly effektivno vzaimodeistvuyut drug s drugom. Eto uproshaet situaciyu, poskol'ku pozvolyaet schitat', chto sily, deistvuyushie na malyi ob'em, prilozheny k ogranichivayushei ego poverhnosti.

Elementarnye deformacii. Koefficient Puassona.

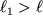
Pri vsem mnogoobrazii sluchaev proizvol'nuyu deformaciyu tela mozhno svesti k dvum elementarnym deformaciyam - rastyazheniyu (szhatiyu) i sdvigu. Obratimsya k opytu. Zakrepim odin konec rezinovogo shnura dlinoi $\ell$ i potyanem za drugoi konec s postoyannoi siloi. Shnur pridet v novoe polozhenie ravnovesiya s dlinoi $\ell_1 > \ell$ (ris. 1.1). Takuyu prosteishuyu deformaciyu mozhno oharakterizovat' otnositel'nym udlineniem

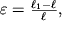$\varepsilon = \frac{\ell_1 - \ell}{\ell},$

(1.1)

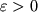
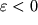
Pri etom rastyazhenie sootvetstvuet $\varepsilon > 0$ , a szhatiyu - $\varepsilon < 0$ .

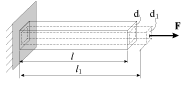Ris. 1.1.

Deformaciyu sdviga mozhno nablyudat' v opyte s rezinovym kubikom, esli zakrepit', naprimer, ego nizhnee osnovanie, a k verhnemu osnovaniyu prilozhit' kasatel'nuyu silu. (ris. 1.2)Deformaciya v etom sluchae budet harakterizovat'sya parametrom

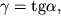$\gamma = {\rm tg} \alpha,$

(1.2)

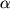
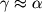
zavisyashim ot ugla sdviga $\alpha$ , kotoryi v bol'shinstve prakticheski vazhnyh sluchaev mal, i $\gamma \approx \alpha$ .

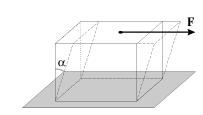Ris. 1.2.

Otmetim takzhe izvestnyi fakt, chto pri rastyazhenii rezinovogo shnura ego poperechnyi razmer d umen'shaetsya do velichiny d₁. Takoe poperechnoe szhatie harakterizuetsya parametrom

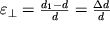$\varepsilon_\perp=\frac{d_1 -d}{d}=\frac{\Delta d}{d}$

(1.3)

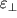
Opytnym putem ustanovleno, chto otnoshenie $\varepsilon_{\perp}$ k $\varepsilon$ priblizitel'no odinakovo dlya raznyh deformacii odnogo i togo zhe materiala. V teorii uprugosti material harakterizuetsya koefficientom Puassona

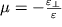$\mu =-\frac{\varepsilon_\perp}{\varepsilon}$

(1.4)

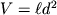
Kakovo chislennoe znachenie koefficienta Puassona? Chtoby otvetit' na etot vopros, poschitaem izmenenie ob'ema rezinovogo shnura. V otsutstvie deformacii ego ob'em $V = \ell d^2$ , ob'em zhe deformirovannogo shnura

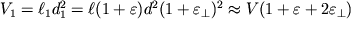$V_1=\ell_1 d^2_1=\ell (1+\varepsilon)d^2(1+\varepsilon_\perp)^2\approx V(1+\varepsilon +2\varepsilon_\perp)$

(1.5)

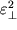
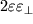
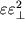
V poslednem vyrazhenii my prenebregli malymi velichinami $\varepsilon_\perp^2$ , $2\varepsilon\varepsilon_\perp$ i $\varepsilon\varepsilon_\perp^2$ . S uchetom (1.4) otnositel'noe izmenenie ob'ema zapishetsya v vide

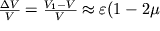$\frac{\Delta V}{V} = \frac{V_1 - V}{V} \approx \varepsilon (1 - 2\mu$

(1.6)

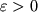
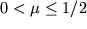
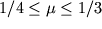
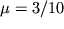
Poskol'ku pri rastyazhenii ( $\varepsilon > 0$ ) ob'em nikogda ne umen'shaetsya, to $0 < \mu \le 1/2$ . Dlya izotropnyh materialov, imeyushih odinakovye mehanicheskie svoistva po vsem napravleniyam, koefficient Puassona $1/4 \le \mu \le 1/3$ , v chastnosti, dlya metallov $\mu = 3/10$ .

Ponyatie o tenzore deformacii

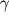
V rassmotrennyh vyshe sluchayah my imeli delo s odnomernymi odnorodnymi deformaciyami rastyazheniya i sdviga (vdol' odnogo napravleniya), gde $\varepsilon$ i $\gamma$ okazyvalis' odnimi i temi zhe dlya vseh elementarnyh ob'emov rezinovogo shnura. Vo mnogih sluchayah situaciya gorazdo slozhnee: s odnoi storony, deformacii menyayutsya ot tochki k tochke (neodnorodnye deformacii), a s drugoi storony ne yavlyayutsya odnomernymi. 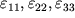Poslednee oznachaet, chto deformacii v nekotoroi tochke P opisyvayutsya tremya deformaciyami rastyazheniya $\varepsilon_{11}, \varepsilon_{22}, \varepsilon_{33}$ malen'kogo kubika s t. P vnutri (ris. 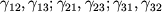1.3) i dvumya sdvigami kazhdoi iz treh granei kubika: $\gamma_{12}, \gamma_{13}; \gamma_{21}, \gamma_{23}; \gamma_{31}, \gamma_{32}$ . Zdes' pervyi indeks i oznachaet, chto gran' kubika perpendikulyarna osi X_i, vtoroi indeks j oznachaet, chto gran' smeshaetsya vdol' osi X_j. Takim obrazom, neodnorodnye deformacii v kazhdoi tochke tela v obshem sluchae harakterizuyutsya naborom 9 velichin deformacii, yavlyayushihsya funkciyami koordinat. Eti devyat' velichin sostavlyayut tenzor deformacii, odnako nezavisimy lish' 6 ego velichin.

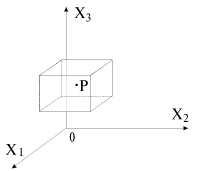Ris. 1.3.

Rassmotrim neskol'ko podrobnee podhod, ispol'zuemyi dlya opisaniya deformacii v nekotoroi tochke P, privodyashii k vvedeniyu ponyatiya tenzor deformacii. Pust' telo nahoditsya k nedeformirovannom sostoyanii, i izvestno polozhenie kazhdoi iz ego chastic, zadavaemyh radius-vektorom r otnositel'no nekotoroi sistemy koordinat kak, naprimer, polozhenie t. P na ris 1.4. Pri deformirovanii vse ego tochki, voobshe govorya, smeshayutsya. Smeshenie kazhdoi tochki mozhno oharakterizovat' vektorom smesheniya u(x₁, x₂, x₃), yavlyayushegosya pri neodnorodnyh deformaciyah funkciei koordinat. Odnako deformacii v tochke budut opredeleny lish' togda, esli izvestno smeshenie sosednih s t. P chastic tela. Takim obrazom, zadanie smesheniya vseh chastic tela polnost'yu opredelyaet ego deformaciyu. V samom dele, rassmotrim dve beskonechno blizkie tochki P(x₁, x₂, x₃) i P'(x₁+dx₁,x₂+dx₂,x₃+dx₃), imeyushie smesheniya u(x₁,x₂,x₃) i u'=u(x₁+dx₁,x₂+dx₂,x₃+dx₃). 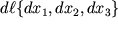Iz risunka netrudno videt', chto esli vzaimnoe raspolozhenie tochek v nedeformirovannom sostoyanii zadavalos' radius-vektorom $d\ell\{dx_1,dx_2,dx_3\}$ proekcii , to v rezul'tate deformacii novoe vzaimnoe raspolozhenie zadaetsya vektorom

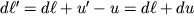$d\ell'=d\ell+u' -u=d\ell+du$

(1.7)

V chastnosti, esli u'=u, to deformacii v t. P otsutstvuyut.

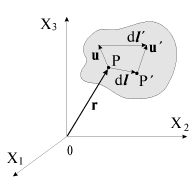Ris. 1.4.

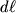
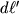
Dlya udobstva opisaniya deformacii vozvedem (1.7) v kvadrat i budem operirovat' modulyami vektorov $d\ell$ i $d\ell'$ .Togda

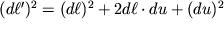$(d\ell')^2=(d\ell)^2+2d\ell\cdot du +(du)^2$

(1.8)

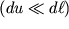
V ravenstve (1.8) prenebrezhem poslednim chlenom v pravoi chasti, poskol'ku snizhaem deformacii malymi $(du\ll d\ell)$ , a proekcii vektora du predstavim v vide summ

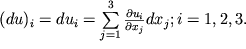$(du)_i=du_i=\sum\limits_{j=1}^3\frac{\partial u_i}{\partial x_j}dx_j; i=1,2,3.$

(1.9)

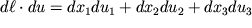
Vyrazhenie (1.9), po sushestvu opisyvaet prirashenie kazhdoi iz treh proekcii vektora smesheniya pri perehode iz t.P v t.P', i soderzhit tri slagaemyh, kazhdoe iz kotoryh est' proizvedenie proizvodnoi funkcii u_i v t.P na prirashenie sootvetstvuyushego argumenta dx_j. Raspisyvaya v (1.8) skalyarnoe proizvedenie v vide $d\ell\cdot du=dx_1 du_1+dx_2 du_2+dx_3 du_3$ i podstavlyaya (1.9) v (1.8), poluchim

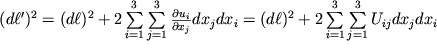$(d\ell')^2=(d\ell)^2+2\sum\limits_{i=1}^3\sum\limits_{j=1}^3 \frac{\partial u_i}{\partial x_j}dx_j dx_i=(d\ell)^2+2\sum\limits_{i=1}^3\sum\limits_{j=1}^3 U_{ij} dx_j dx_i$

(1.10)

gde, po opredeleniyu,

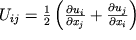$U_{ij}=\frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right)$

(1.11)

- tenzor deformacii. Iz ego opredeleniya vidno, chto on yavlyaetsya simmetrichnym tenzorom (U_ij= U_ji). Dlya opisaniya deformacii v kazhdoi t.P mozhno vybrat' takuyu sistemu koordinat, v kotoroi tol'ko tri diagonal'nye komponenty tenzora U₁₁, U₂₂ i U₃₃ otlichny ot nulya. Kak i v sluchae privedeniya tenzora inercii k glavnym osyam, umestno napomnit', chto dlya kazhdoi tochki tela P sushestvuyut svoi tri glavnye osi, otnositel'no kotoryh formula (1.10) imeet naibolee prostoi vid:

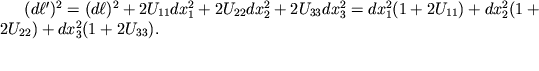$(d\ell')^2=(d\ell)^2 + 2U_{11}dx_1^2+ 2U_{22}dx_2^2 + 2U_{33}dx_3^2 = dx_1^2 (1+2U_{11}) + dx_2^2 (1+2U_{22}) + dx_3^2 (1+2U_{33}).$

(1.12)

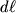
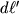
V kachestve primera rassmotrim deformaciyu sdviga v rezinovom kube, izobrazhennom na ris. 1.2. Dlya udobstva nanesem na ego bokovuyu gran' pryamougol'nuyu setku, razbivayushuyu etu gran' na malen'kie kvadratiki so storonami, parallel'nymi ee diagonalyam (ris. 1.5a). Pri deformacii kvadratiki prevrashayutsya v pryamougol'niki (ris. 1.5b). Esli pod $d\ell$ i $d\ell'$ ponimat' dliny diagonalei elementarnyh kvadratika i pryamougol'nika sootvetstvenno, to eti dliny mozhno svyazat' formuloi (1.12) tol'ko v sisteme koordinat, osi kotoroi X₁ i H₂ napravleny vdol' reber elementarnyh yacheek (os' H₃ perpendikulyarna ploskosti chertezha).

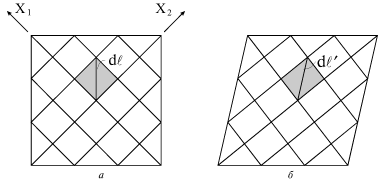Ris. 1.5.

Obobshaya poluchennyi rezul'tat, sleduet skazat', chto pri proizvol'nyh deformaciyah glavnye osi v lyuboi tochke R dolzhny byt' napravleny parallel'no rebram elementarnogo pryamougol'nogo parallepipeda, kotoryi pri deformacii ostaetsya pryamougol'nym parallepipedom. Deformacii sdviga otnositel'no glavnyh osei koordinat otsutstvuyut. Nizhe my ustanovim svyaz' mezhdu deformaciyami sdviga i nediagonal'nymi komponentami tenzora deformacii. Vyyasnim dalee fizicheskii smysl diagonal'nyh komponent U₁₁, U₂₂ i U₃₃. Otnositel'noe udlinenie kazhdoi iz granei prizmy ravno sootvetstvuyushei diagonal'noi komponente tenzora deformacii. V samom dele

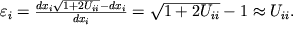$\varepsilon_i=\frac{dx_i \sqrt{1+2U_{ii}}-dx_i}{dx_i}=\sqrt{1+2U_{ii}}-1\approx U_{ii}.$

(1.13)

Pust' v okrestnosti t. P(x₁,x₂,x₃) deformacii takovy, chto kubik so storonami dx₁, dx₂ i dx₃ prevrashaetsya v parallelepiped.Dlya naglyadnosti rassmotrim kratinu deformacii v ploskosti X₁ X₂. Smesheniya vershin kvadrata pri deformacii izobrazheny sootvetstvuyushimi vektorami. Dliny pryamougol'nika v napravlenii glavnyh osei X₁ i X₂ izmenilis' do velichin

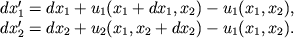$\begin{array}{l} dx'_1=dx_1 + u_1(x_1+dx_1,x_2)-u_1(x_1,x_2),\\ dx'_2=dx_2 + u_2(x_1,x_2+dx_2)-u_1(x_1,x_2). \end{array}$

(1.14)

Iz (1.14) legko vychislyayutsya otnositel'nye udlineniya:

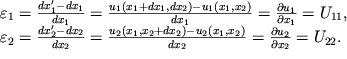$\begin{array}{l} \varepsilon_1=\frac{dx'_1-dx_1}{dx_1}=\frac{u_1(x_1+dx_1,dx_2)-u_1(x_1,x_2)}{dx_1}=\frac{\partial u_1}{\partial x_1}=U_{11},\\ \varepsilon_2=\frac{dx'_2-dx_2}{dx_2}=\frac{u_2(x_1,x_2+dx_2)-u_2(x_1,x_2)}{dx_2}=\frac{\partial u_2}{\partial x_2}=U_{22}. \end{array}$

(1.15)

S ispol'zovaniem sootnosheniya (1.13) legko takzhe svyazat' izmenenie elementarnogo ob'ema s diagonal'nymi komponentami tenzora. Ob'em elementarnogo parallelepipeda

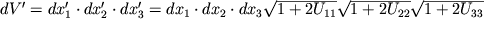
$dV'=dx'_1\cdot dx'_2 \cdot dx'_3 = dx_1\cdot dx_2 \cdot dx_3 \sqrt{1+2U_{11}}\sqrt{1+2U_{22}}\sqrt{1+2U_{33}}$

(1.16)

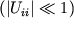
i takzhe izmenyaetsya pri deformaciyah. Otnositel'noe izmenenie etogo ob'ema pri malyh deformaciyah $(|U_{ii}|\ll 1)$ , kak sleduet iz (1.16), ravno:

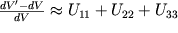
$\frac{dV'-dV}{dV}\approx U_{11}+U_{22}+U_{33}$

(1.17)

Vazhno otmetit', chto pri sdvige ob'em tela ne menyaetsya. Poetomu pri deformaciyah sdviga summa diagonal'nyh komponent tenzora deformacii (inogda upotreblyayut termin "sled tenzora"), privedennogo k glavnym osyam, ravna nulyu (sm. nizhe).

Ris. 1.6.

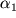
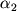
Poyasnim dalee fizicheskii smysl nediagonal'nyh komponent tenzora deformacii. Pust' parallelepiped ispytyvaet deformaciyu, v rezul'tate kotoroi pryamougol'nik na ris. 1.6 prevrashaetsya v parallelogramm. V rassmatrivaemom primere my otvlekaemsya, kak i ranee, ot smesheniya chastic vdol' osi X₃. Legko dalee poschitat' ugly $\alpha_1$ i $\alpha_2$ , na kotorye povernulis' storony parallelogramma otnositel'no storon parallelepipeda. 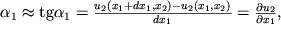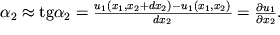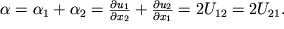Oni, ochevidno, ravny $\alpha_1\approx {\rm tg} \alpha_1 = \frac{u_2(x_1+dx_1,x_2)-u_2(x_1,x_2)}{dx_1}=\frac{\partial u_2}{\partial x_1},$ $\alpha_2\approx {\rm tg} \alpha_2 = \frac{u_1(x_1,x_2+dx_2)-u_1(x_1,x_2)}{dx_2}=\frac{\partial u_1}{\partial x_2}.$ Togda ugol sdviga $\alpha=\alpha_1 + \alpha_2 = \frac{\partial u_1}{\partial x_2} + \frac{\partial u_2}{\partial x_1} = 2 U_{12} = 2 U_{21}.$ Takim obrazom, nediagonal'nye komponenty tenzora deformacii opredelyaet sdvigovye ugly $\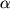alpha$ v sootvetstvuyushih ploskostyah.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce