Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Uprugie tela

Kak uzhe otmechalos' vyshe, pri deformaciyah voznikayut vnutrennie napryazheniya, sily kotoryh, v obshem sluchae, zavisyat ne tol'ko ot deformacii, no i ot skorostei, s kotorymi eti deformacii proishodyat. V etom legko ubedit'sya, esli vzyat' polimernoe veshestvo, kotoroe pri obychnyh usloviyah medlenno rastekaetsya podobno zamazke, prinimaya formu sosuda, v kotorom ono nahoditsya. Mozhno bez osobyh usilii izmenit' ego formu, esli delat' eto medlenno. Odnako, esli vylepit' sharik, to legko obnaruzhit', chto takoi sharik obladaet horoshimi uprugimi svoistvami, podskakivaya prakticheski posle udara ob pol na tu zhe vysotu, s kotoroi on byl broshen bez nachal'noi skorosti. Etot opyt pokazyvaet, chto sily deformacii, podobno silam vyazkogo treniya, vozrastayut po mere uvelicheniya skorosti deformacii. V ryade prakticheski vazhnyh sluchaev sily napryazheniya opredelyayutsya tol'ko deformaciyami. Takie tela, v kotoryh eto imeet mesto, nazyvayutsya absolyutno uprugimi telami, ili uprugimi telami. Zamechatel'nym svoistvom takih tel yavlyaetsya sposobnost' polnost'yu vosstanavlivat' svoyu formu posle snyatiya vneshnih usilii, prikladyvaemyh k telu. Rassmotrim, naprimer, rastyazhenie (ili szhatie) sterzhnya (ris. 1.1) s siloi F, prilozhennoi perpendikulyarno k torcevoi grani s ploshad'yu secheniya S. Opyt pokazyvaet, chto pri posledovatel'nom vozrastanii nagruzki vnachale deformacii razvivayutsya ravnomerno po dline sterzhnya i rastut proporcional'no nagruzke, t.e.

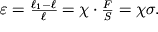
$\varepsilon = \frac{\ell_1 - \ell}{\ell} = \chi \cdot \frac{F}{S} = \chi\sigma.$

(1.18)

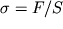
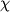
Velichina $\sigma= F/S$ nazyvaetsya normal'nym napryazheniem v torcevom sechenii sterzhnya. Proporcional'nost' deformacii $\varepsilon$ sootvetstvuyushim napryazheniyam vyrazhaet zakon Guka. Koefficient proporcional'nosti $\chi$ nazyvaetsya koefficientom udlineniya i dlya kazhdogo materiala opredelyaetsya opytnym putem. 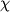Tak kak chislennye znacheniya $\varepsilon$ gorazdo men'she $\varepsilon$ , to $\chi$ - ves'ma malaya velichina. 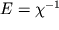Poetomu obychno vvodyat modul' uprugosti (modul' Yunga) $E=\chi^{-1}$ , i zakon Guka okonchatel'no zapisyvayut v vide

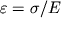
$\varepsilon = \sigma / E$

(1.19)

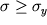
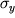
Opyt pokazyvaet, chto etot zakon vypolnyaetsya lish' v opredelennom intervale napryazhenii. Esli rastyagivat' sterzhen', posledovatel'no uvelichivaya ot nulya vozrastayushuyu silu, to kazhdyi raz, posle snyatiya nagruzki, deformaciya ischezaet. Odnako pri nekotorom napryazhenii $\sigma \ge \sigma_y$ poyavlyaetsya zametnoe ostatochnoe udlinenie. Eto napryazhenie $\sigma_y$ nazyvaetsya predelom uprugosti. Na ris. (1.7) izobrazhena zavisimost' deformacii ot napryazhenii, nazyvaemaya diagrammoi rastyazhenii. 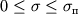Sleduet otmetit', chto zakon Guka vypolnyaetsya tol'ko v chasti oblasti uprugosti - oblasti proporcional'nosti, kogda $0\le\sigma\le\sigma_{p}$ .

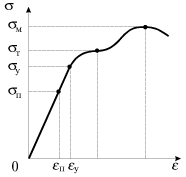Ris. 1.7.

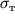
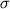
Pri vozrastanii nagruzki nablyudaetsya yavlenie tekuchesti, t.e. vnezapnyi rost udlineniya obrazca pri postoyannoi nagruzke $\sigma_t$ , nazyvaemoi predelom tekuchesti. Otmetim, chto techenie materiala proishodit ravnomerno po vsei dline sterzhnya. Za predelami oblasti tekuchesti dal'neishee udlinenie sterzhnya soprovozhdaetsyauvelicheniem $\sigma$ . Odnako deformacii budut raspredeleny uzhe neodinakovo po dine sterzhnya (ris. 1.8.) - v nekotorom meste mozhno zametit' obrazovanie sheiki. 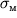Pri napryazhenii $\sigma_m$ , nazyvaemom predelom prochnosti, v etom oslablennom sechenii proishodit razryv.

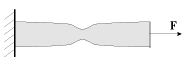Ris. 1.8.

To napryazhenie, kotoroe dannyi material mozhet vyderzhat' na praktike, ne razrushayas' i ne poluchaya opasnoi deformacii, nazyvayut dopustimym i oboznachayut $[\sigma]$ . Obychno $[\sigma]<\sigma_p$ , i vse raschety provodyat na osnove zakonov Guka. Chtoby obespechit' prochnost' pri vseh obstoyatel'stvah dopustimoe napryazhenie vybiraetsya kak chast' predela prochnosti, v chastnosti, dlya metallov $[\sigma]=0.2 \sigma_m$ , a dlya dereva $[\sigma]=0.1 \sigma_m$ . Sleduet otmetit', chto naibol'shie deformacii, kotorye mozhet vyderzhat' material, ne opredelyayutsya protyazhennost'yu oblasti tekuchesti. Esli oblast' tekuchesti velika, to material nazyvaetsya plastichnym. Takoi material, kak, naprimer, stal', sposoben vyderzhivat' bol'shie nagruzki bez razrusheniya. Naoborot, esli oblast' tekuchesti nevelika, to etot material hrupok. 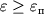Hrupkie materialy, kak chugun, naprimer, razrushayutsya pri deformaciyah $\varepsilon\ge\varepsilon_p$ . 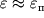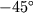Odnako v ryade sluchaev plastichnye materialy mogut razrushat'sya i pri malyh deformaciyah $\varepsilon\approx\varepsilon_p$ (naprimer, stal' pri temperature nizhe $-45^{\circ}$ S). Analogichnymi svoistvami obladayut i sdvigovye deformacii. V chastnosti, v oblasti proporcional'nosti svyaz' mezhdu deformaciyami sdviga i kasatel'nym napryazheniem (ris. 1.2) zadaetsya sootnosheniem

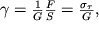
$\gamma = \frac{1}{G}\frac{F}{S}=\frac{\sigma_\tau}{G},$

(1.20)

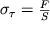
v kotorom $\sigma_\tau=\frac{F}{S}$ - kasatel'noe napryazhenie, analogichnoe po smyslu vvedennomu vyshe normal'nomu napryazheniyu, a G - modul' sdviga, yavlyayushiisya, kak i modul' Yunga, takzhe harakteristikoi materiala.

Material	Modul' uprugosti E	Modul' sdviga G	Predel proporcional'nosti 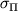$\sigma_P$	Predel tekuchesti 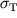$\sigma_T$	Predel prochnosti pri rastyazhenii 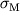$\sigma_M$
Svarochnaya stal'	2000	770	1,3...1,6	1,8...2,6	3,3...4,0
Pruzhinnaya stal' nezakalennaya	2200	850	5,0 i vyshe	-	do 10 i vyshe
Pruzhinnaya stal' zakalennaya	2200	850	8,5 i vyshe	-	do 17
Med'	1100...1300	415...440	-	0,7	22
Seryi chugun	750...1050	290...400	-	-	1,2...2,4
Svinec	140...180	55...80	-	0,05	0,14...0,18

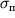
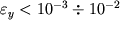
V tablice privedeny harakteristiki uprugosti i prochnosti nekotoryh materialov. Iz etoi tablicy mozhno sdelat' dva vazhnyh vyvoda. Vo-pervyh, poskol'ku predel proporcional'nosti $\sigma_p$ na 2-3 poryadka men'she modulya uprugosti, to v oblasti uprugosti deformacii $\varepsilon_y<10^{-3}\div 10^{-2}$ .

Ris. 1.9.

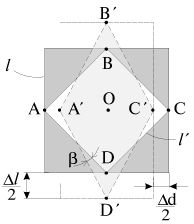
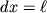
Vo-vtoryh, prosmatrivaetsya svyaz' mezhdu velichinoi modulya Yunga E i modulya sdviga G - chem bol'she E, tem bol'she i G. Eto ne sluchaino, t.k. mezhdu obeimi velichinami sushestvuet zhestkaya svyaz'. Chtoby ee ustanovit', rassmotrim rastyazhenie malen'kogo kubika s dlinoi storony $dx=\ell$ , kak eto bylo izobrazheno na ris. 1.9. Obratim vnimanie, odnako, na to, chto kvadratnaya gran' ABCD parallelepipeda, nahodyashegosya vnutri rassmatrivaemogo kubika, prevrashaetsya pri deformaciyah v rombicheskuyu gran' A'B'C'D'. Sovershenno yasno, chto parallelepiped ispytyvaet sdvigovuyu deformaciyu, a ego ob'em pri etom prakticheski ne izmenilsya (sm. takzhe formulu (1.17)). 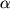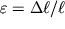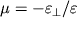Velichinu ugla sdviga $\alpha$ mozhno legko svyazat' s deformaciei udlineniya $\varepsilon=\Delta \ell / \ell$ i koefficientom Puassona $\mu=-\varepsilon_\perp / \varepsilon$ . Iz treugol'nika A'OD' sleduet, chto

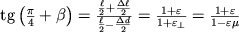
${\rm tg}\left( \frac{\pi}{4}+\beta \right) = \frac{\frac{\ell}{2}+\frac{\Delta\ell}{2}}{\frac{\ell}{2}-\frac{\Delta d}{2}} = \frac{1+\varepsilon}{1+\varepsilon_\perp}=\frac{1+\varepsilon}{1-\varepsilon\mu}$

(1.21)

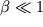
Poskol'ku $\beta\ll 1$ , to

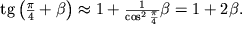
${\rm tg}\left( \frac{\pi}{4}+\beta \right) \approx 1 + \frac{1}{\cos^2\frac{\pi}{4}}\beta = 1 + 2 \beta.$

(1.22)

Priravnivaya pravye chasti (1.21) i (1.22), nahodim

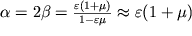
$\alpha=2\beta=\frac{\varepsilon(1+\mu)}{1-\varepsilon\mu} \approx \varepsilon(1+\mu)$

(1.23)

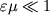
V poslednei formule uchteno, chto $\varepsilon\mu\ll 1$ .

Ris. 1.10.

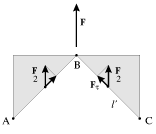
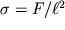
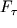
Sila F, rastyagivayushaya kubik (ris. 1.10), sozdaet normal'noe napryazhenie $\sigma=F/\ell^2$ . Eto napryazhenie peredaetsya na grani AB i BC parallelepipeda, odnako sily, deistvuyushie na kazhduyu iz ego granei, imeyut ne tol'ko normal'nuyu k grani, no i napravlennuyu vdol' grani parallel'nuyu sostavlyayushuyu $F_\tau$ . Kasatel'noe napryazhenie okazyvaetsya pri etom ravnym

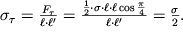
$\sigma_\tau=\frac{F_\tau}{\ell\cdot\ell'}=\frac{\frac{1}{2}\cdot\sigma\cdot\ell\cdot\ell\cos\frac{\pi}{4}}{\ell\cdot\ell'}=\frac{\sigma}{2}.$

(1.24)

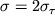
Poskol'ku deformacii $\varepsilon$ v formule (1.23) proporcional'ny napryazheniyam, a $\sigma=2\sigma_\tau$ , to

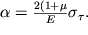
$\alpha = \frac{2 (1+\mu}{E}\sigma_\tau.$

(1.25)

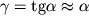
Sravnivaya poslednee ravenstvo s sootnosheniem (1.20) pri uchete, chto $\gamma={\rm tg}\alpha\approx\alpha$ , nahodim iskomuyu svyaz' mezhdu modulyami Yunga i sdviga:

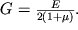
$G=\frac{E}{2(1+\mu)}.$

(1.26)

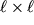
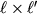
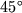
V rassmotrennom primere sleduet obratit' vnimanie na to, chto velichina i napravlenie sily, prilozhennoi k nekotoroi ploshadke, zavisit ot orientacii i velichiny etoi ploshadki. Tak, na gran' $\ell\times\ell$ kuba deistvuet sila F, perpendikulyarnaya k grani, v to vremya kak na gran' parallelepipeda $\ell\times\ell'$ deistvuet sila F/2, napravlennaya pod uglom $45^\circ$ k etoi grani. Etot chastnyi vyvod poluchit dalee obobshenie pri obsuzhdenii sposobov zadaniya sil, deistvuyushih na kazhdyi iz elementov tela. Posmotrim, chto budet proishodit' s tem zhe kubikom, esli ego rastyagivat' odnovremenno silami, prilozhennymi ko vsem ego granyam. V etom sluchae otnositel'nye udlineniya kazhdoi iz ego storon budet zadavat'sya sootnosheniyami:

$\varepsilon_1=\frac{\sigma_1}{E}-\frac{\varepsilon_2}{\mu^{-1}}-\frac{\varepsilon_3}{\mu^{-1}}=\frac{\sigma_1-(\sigma_2 + \sigma_3)\mu}{E},$

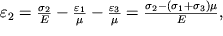$\varepsilon_2=\frac{\sigma_2}{E}-\frac{\varepsilon_1}{\mu}-\frac{\varepsilon_3}{\mu}=\frac{\sigma_2-(\sigma_1 + \sigma_3) \mu}{E},$

(1.27)

$\varepsilon_3=\frac{\sigma_3}{E}-\frac{\varepsilon_2}{\mu}-\frac{\varepsilon_3}{\mu}=\frac{\sigma_3-(\sigma_1 + \sigma_2) \mu}{E}.$

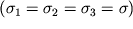
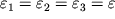
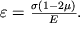
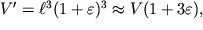
Formuly (1.27) opisyvayut deformacii kubika pri ego vsestoronnem rastyazhenii ili szhatii. Esli napryazheniya odinakovy $(\sigma_1=\sigma_2=\sigma_3=\sigma)$ , to deformacii takzhe budut odinakovy: $\varepsilon_1=\varepsilon_2=\varepsilon_3=\varepsilon$ , i $\varepsilon=\frac{\sigma(1-2 \mu)}{E}.$ V rezul'tate vsestoronnei deformacii novyi ob'em kubika stanet ravnym $V'=\ell^3(1+\varepsilon)^3 \approx V(1+3\varepsilon),$ a ego otnositel'noe izmenenie sostavit velichinu

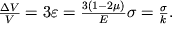
$\frac{\Delta V}{V} = 3\varepsilon = \frac{3(1-2\mu)}{E}\sigma=\frac{\sigma}{k}.$

(1.28)

Parametr

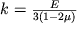
$k = \frac{E}{3(1-2\mu)}$

(1.28)

nazyvaetsya modulem vsestoronnego szhatiya i igraet vazhnuyu rol' v teorii uprugosti. Vazhno otmetit', chto hrupkie materialy, podvergnutye vsestoronnemu davleniyu, na kotoroe dopolnitel'no nakladyvaetsya rastyazhenie, szhatie ili sdvig, obnaruzhivayut znachitel'nye plasticheskie deformacii. Takie deformacii igrayut sushestvennuyu rol', naprimer, v processah obrazovaniya rel'efa zemnoi kory: granity i bazal'ty, hrupkie v obychnyh usloviyah, tekut pod deistviem kolossal'nogo davleniya v glubinnyh sloyah Zemli. Deformacii rastyazheniya i sdviga voznikayut v prakticheski vazhnyh sluchayah izgibov balok stroitel'nyh konstrukcii i okruzhivaniya valov mashin i mehanizmov.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce