Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Izgib balok

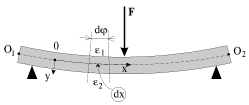Ris. 1.11.

Balka, t.e. sterzhen', ispytyvayushii izgib, deformiruetsya takim obrazom, chto pervonachal'no pryamaya os' balki O₁O₂ stanovitsya krivolineinoi; eta os' nazyvaetsya uprugoi liniei (ris. 1.11). Rassmotrim izgib balki pod deistviem vneshnei sily F, prenebregaya ee vesom. Vse volokna, lezhashie nizhe etoi linii, udlinyayutsya (v nih voznikayut rastyagivayushie napryazheniya), a volokna, lezhashie vyshe etoi linii, szhimayutsya (v nih voznikayut szhimayushie napryazheniya). Mezhdu rastyanutymi voloknami nahoditsya neitral'nyi sloi. 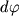Pri etom dva, pervonachal'no parallel'nye secheniya i nahodyashiesya na rasstoyanii dx drug ot druga, pri izgibe obrazuyut nekotoryi ugol $d\varphi$ . Dlya udobstva opisaniya raspredeleniya deformacii i napryazhenii svyazhem so sterzhnem sistemu koordinat s nachalom v nekotoroi tochke O uprugoi linii O₁O₂ i osyami x i y, napravlennymi vdol' uprugoi linii i v poperechnom sechenii sootvetstvenno (sm. ris. 1.11). 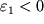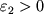Legko videt', chto deformacii v nekotorom sechenii x=const lineino narastayut vdol' osi y ot $\varepsilon_1<0$ do $\varepsilon_2>0$ . Eto daet osnovanie v sootvetstvii s zakonom Guka zapisat' raspredelenie napryazhenii v vide

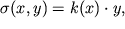
$\sigma(x,y)=k(x)\cdot y,$

(1.30)

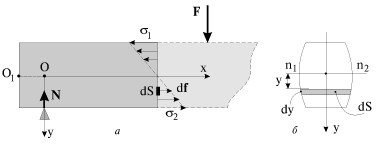
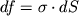
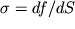
gde k - neizvestnyi koefficient proporcional'nosti, menyayushiisya, voobshe govorya, ot secheniya k secheniyu. Raspredelenie napryazhenii (1.30) v proizvol'nom sechenii sterzhnya udobno izobrazit' graficheski, esli v kazhdoi tochke secheniya vosstanovit' perpendikulyarnyi k nemu vektor, myslenno ravnyi sile, deistvuyushei na ploshadku dS: $df=\sigma \cdot dS$ (ris.1.12a), t.e. $\sigma=df/dS$ .

Ris. 1.12.

Rassmotrim ravnovesie chasti balki, raspolozhennoi sleva ot secheniya. Nachalo koordinat pomestim v sechenie, vdol' kotorogo deistvuet sila reakcii opory. Predpolozhim, chto balka imeet vertikal'nuyu ploskost' simmetrii, kak eto izobrazheno na ris. 1.12 b, i vneshnie sily lezhat v etoi ploskosti. Neitral'nyi sloi peresekaet sechenie balki po pryamoi n₁n₂. Dlya ravnovesiya etogo kuska balki neobhodimo, chtoby vypolnyalis' sleduyushie izvestnye iz statiki usloviya. Vo-pervyh summa vseh gorizontal'nyh sil dolzhna byt' ravna nulyu, t.e.

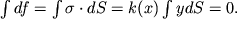
$\int df=\int \sigma\cdot dS= k(x)\int y dS=0.$

(1.31)

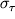
Poskol'ku integral (1.31) vychislyaetsya v poperechnom sechenii balki, to ponyatno, chto neitral'naya os' n₁n₂, na kotoroi lezhit nachalo koordinat, dolzhna prohodit' cherez centr mass poperechnogo secheniya balki. Vo-vtoryh, summa vseh vertikal'nyh sil mozhet byt' ravna nulyu, esli v sechenii, krome izobrazhennyh normal'nyh napryazhenii, budut deistvovat' i kasatel'nye napryazheniya $\sigma_\tau$ , chtoby skompensirovat' silu reakcii opory N, t.e.

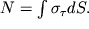
$N=\int \sigma_\tau dS.$

(1.32)

V bol'shinstve sluchaev kasatel'nye napryazheniya pri izgibe maly po sravneniyu s normal'nymi i pri raschete balki na prochnost' ne uchityvayutsya. V tret'ih, summa momentov vseh sil otnositel'no lyuboi tochki dolzhna byt' ravna nulyu. Esli v kachestve takoi tochki vybrat' centr mass rassmatrivaemogo secheniya, to eto uslovie zapishetsya v vide.

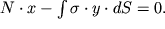
$N\cdot x -\int \sigma\cdot y \cdot dS = 0.$

(1.33)

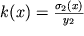
Esli podstavit' syuda raspredelenie napryazhenii (1.30), gde koefficient proporcional'nosti $k(x)=\frac{\sigma_2(x)}{y_2}$ (y₂ - rasstoyanie mezhdu neitral'nym sloem i naibolee rastyanutym nizhnim voloknom), to my prihodim k usloviyu

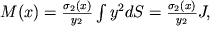
$M(x)=\frac{\sigma_2(x)}{y_2}\int y^2 dS = \frac{\sigma_2(x)}{y_2}J,$

(1.34)

gde

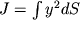
$J=\int y^2 dS$

(1.35)

moment inercii poperechnogo secheniya otnositel'no central'noi osi n₁n₂, M(x)=N*x - moment sily reakcii. Otnoshenie J/y₂ zavisit ot razmerov i formy secheniya i nazyvaetsya osevym momentom soprotivleniya:

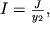
$I=\frac{J}{y_2},$

(1.36)

a uravneniya (1.34) mozhno predstavit' v vide

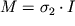
$M=\sigma_2\cdot I$

(1.37)

Ris. 1.13.

Dlya rascheta prochnosti balok neobhodimo znat' raspredelenie napryazhenii , voznikayushih pri izvestnyh momentah vneshnih sil, chto mozhet byt' polucheno iz (1.34) v vide

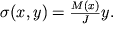
$\sigma(x,y)=\frac{M(x)}{J}y.$

(1.38)

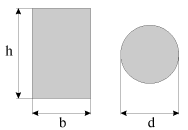
Momenty inercii poperechnyh sechenii (pryamougol'nogo i krugovogo) ravny

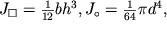
$J_{\Box}=\frac{1}{12} bh^3 , J_{\circ}=\frac{1}{64}\pi d^4 ,$

(1.39)

a sootvetstvuyushie im osevye momenty soprotivleniya -

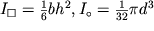
$I_{\Box}=\frac{1}{6} bh^2 , I_{\circ}=\frac{1}{32}\pi d^3$

(1.40)

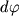
Iz (1.37) sleduet, chto prochnost' balok vozrastaet pri uvelichenii osevogo momenta soprotivleniya, prichem, kak sleduet iz (1.40), prochnost' balki pryamougol'nogo secheniya dostigaetsya effektivnee za schet uvelicheniya ee vysoty h. Poluchennye rezul'taty pozvolyayut rasschitat' napravlenie osevoi linii balki. 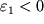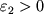Elementarnyi ugol $d\varphi$ , na kotoryi povernulis' secheniya x i x+dx, ochevidno, svyazan s dvumya deformaciyami $\varepsilon_1<0$ i $\varepsilon_2>0$ krainih volokon sootnosheniem

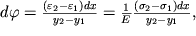
$d\varphi=\frac{(\varepsilon_2-\varepsilon_1)dx}{y_2-y_1}=\frac{1}{E}\frac{(\sigma_2-\sigma_1)dx}{y_2-y_1},$

(1.41)

gde y₂-y₁- rasstoyanie mezhdu krainimi voloknami. Podstavlyaya v (1.41) napryazhenie (1.38), poluchim

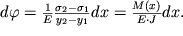
$d\varphi= \frac{1}{E}\frac{\sigma_2-\sigma_1}{y_2-y_1}dx=\frac{M(x)}{E\cdot J}dx.$

(1.42)

V chastnosti, legko rasschitat' izgib nevesomoi gorizontal'noi balki, vystupayushei iz steny (konsol'noi balki) na rasstoyanie $\ell$ , k koncu kotoroi prilozhena vertikal'naya sila F(ris.1.14). Kak sleduet iz (1.42), v proizvol'nom sechenii x

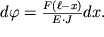
$d\varphi=\frac{F(\ell-x)}{E\cdot J}dx.$

(1.43)

Ris. 1.14.

Esli os' balki v kazhdom sechenii smestilas' vniz na rasstoyanie u(x), to, ochevidno, ugol naklona osi balki k gorizontal'noi osi v sechenii x

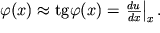
$\varphi(x)\approx {\rm tg} \varphi(x)= \left. \frac{du}{dx}\right|_x.$

(1.44a)

V sechenii x+dx ugol naklona neskol'ko bol'she:

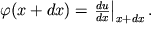
$\varphi (x+dx)= \left. \frac{du}{dx}\right|_{x+dx}.$

(1.44b)

Prirashenie etogo ugla

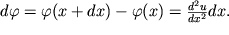
$d\varphi=\varphi(x+dx)-\varphi(x)=\frac{d^2 u}{dx^2}dx.$

(1.45)

Priravnivaya pravye chasti (1.45) i (1.43), poluchaem uravnenie:

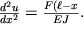
$\frac{d^2 u}{dx^2}=\frac{F(\ell-x}{EJ}.$

(1.46)

Integriruya dva raza pri uslovii, chto u(0)=0 (konec zakreplen), poluchaem iskomoe iskrivlenie balki v vide

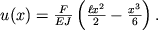
$u(x)=\frac{F}{EJ}\left( \frac{\ell x^2}{2}-\frac{x^3}{6}\right).$

(1.47)

V chastnosti, smeshenie konca balki pod deistviem sily F, nazyvaemoe streloi progiby, okazyvaetsya ravnym

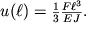
$u(\ell)=\frac{1}{3}\frac{F\ell^3}{EJ}.$

(1.48)

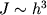
Esli balka imeet pryamougol'noe sechenie, to ee strela progiba ochen' bystro umen'shaetsya po mere uvelicheniya vysoty balki h, poskol'ku $J\sim h^3$ . Dlya ekonomii materiala inogda ispol'zuyut pustotelye balki. Takaya balka znachitel'no legche cel'noi, a ee osevoi moment soprotivleniya (sm. 1.36) ostaetsya dostatochno bol'shim. Dlya povysheniya zhestkosti ispol'zuyut konstrukcii, nazyvaemye fermami (ris. 1.15). Fermy - eto dostatochno legkie azhurnye konstrukcii, vysota kotoryh, v sil'noi stepeni opredelyayushaya moment soprotivleniya, mozhet dostigat' desyatkov metrov.

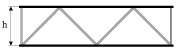Ris. 1.15.

Fermy - eto dostatochno legkie azhurnye konstrukcii, vysota kotoryh, v sil'noi stepeni opredelyayushaya moment soprotivleniya, mozhet dostigat' desyatkov metrov. V kachestve primera na ris. 1.16 pokazana tipichnaya konstrukciya podvesnogo mosta. Neobhodimaya zhestkost' takogo mosta obespechivaetsya fermami, sostoyashimi iz zhestkih elementov i trosov. Rekordnuyu dlinu 3910 metrov imeet most, soedinyayushii dva ostrova v Yaponii. Dlina ego central'nogo proleta L sostavlyaet 1990 metrov pri vysote opor N = 297 metrov.

Ris. 1.16.

Kruchenie valov

Deformacii sdviga voznikayut pri skruchivanii valov mashin i mehanizmov, kogda posredstvom vala peredaetsya vrashatel'noe usilie ot odnoi chasti mehanizma k drugoi. Esli, naprimer, nizhnee osnovanie vala, izgotovlennoe v vide kruglogo sterzhnya radiusa R i dliny $\ell$ , zakrepit', a k verhnemu osnovaniyu prilozhit' zakruchivayushii moment vneshnih sil M, to val deformiruetsya. Na ris. 1.17 izobrazheny deformiruemyi val i deformaciya sdviga elementarnogo ob'ema. 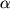Ochevidno, chto ugol sdviga $\alpha$ zavisit ot udaleniya etogo ob'ema ot osi vala. 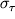Kasatel'nye napryazheniya $\sigma_\tau$ , otvetstvennye za eti deformacii, sozdayut v sechenii moment uprugih sil, ravnyi

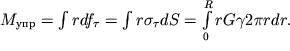
$M_{upr}= \int rdf_\tau=\int r\sigma_\tau dS= \int\limits_0^R rG\gamma 2\pi r dr.$

(1.49)

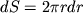
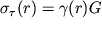
Zdes' uchteno, chto ploshad' elementarnogo kol'ca radiusa r i tolshinoi dr ravna: $dS=2\pi rdr$ , a $\sigma_\tau(r)=\gamma(r)G$ .

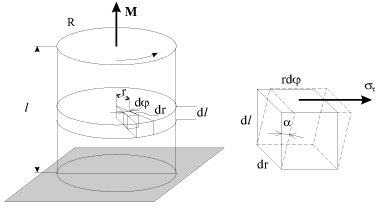Ris. 1.17.

Iz usloviya ravnovesiya chasti vala, nahodyashegosya, naprimer, vyshe ot rassmatrivaemogo secheniya, sleduet, chto

M_upr=M

(1.50)

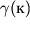
i M_upr ne zavisit ot vybora secheniya vala. Zavisimost' $\gamma(k)$ dolzhna byt' lineinoi funkciei rasstoyaniya r, t.e.

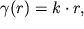
$\gamma(r)=k\cdot r,$

(1.51)

gde neizvestnyi koefficient proporcional'nosti k mozhet byt' opredelen iz (1.49) pri uchete (1.50)

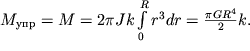
$M_{upr}=M=2\pi J k \int\limits_0^R r^3 dr = \frac{\pi G R^4}{2}k.$

(1.52)

Takim obrazom, sdvigovye deformacii

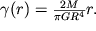
$\gamma(r)=\frac{2 M }{\pi G R^4 }r.$

(1.53)

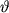
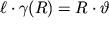
Oni proporcional'ny momentu vneshnih sil i obratno proporcional'ny chetvertoi stepeni R. Iz poslednego sootnosheniya legko poschitat' ugol krucheniya $\vartheta$ , na kotoryi povernetsya verhnee osnovanie sterzhnya otnositel'no nizhnego. Iz ochevidnogo ravenstva $\ell\cdot \gamma(R)=R\cdot \vartheta$ s uchetom (1.53) nahodim

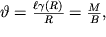
$\vartheta=\frac{\ell \gamma(R)}{R}=\frac{M}{B},$

(1.54)

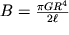
gde $B=\frac{\pi G R^4}{2\ell}$ - modul' krucheniya, zavisyashii ot razmerov vala i modulya sdviga materiala, iz kotorogo val izgotovlen. Dlya sozdaniya zhestkih valov neobhodimo uvelichivat' diametr i sokrashat' dlinu. Dlya ekonomii materiala valy chasto delayut pustotelymi, obespechivaya pri etom vysokuyu zhestkost' vala. V ryade sluchaev, naoborot, ispol'zuyut valy, izgotovlennye v vide tonkih nitei, kak, naprimer, niti podvesa krutil'nyh vesov, ispol'zuemyh Kulonom v opytah po issledovaniyu elektrostaticheskogo vzaimodeistviya i P.N.Lebedevym - v opytah po izmereniyu davleniya sveta. V etih opytah tonkie kvarcevye niti zakruchivalis' na znachitel'nye ugly pri deistvii nichtozhno malyh momentov sil, chto, konechno, Obespechivaet vysokuyu chuvstvitel'nost' krutil'nyh vesov. Otmetim, chto na praktike chasto razlichnye stroitel'nye konstrukcii (balki, fermy i dr.) dolzhny obladat' dostatochnoi soprotivlyaemost'yu kak k izgibu, tak i krucheniyu. Primerom takih konstrukcii yavlyaetsya zheleznodorozhnyi rel's, balka dvuhtavrovogo secheniya, shveller i dr.

Ris. 1.18.

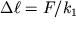
Interesno otmetiit', chto pri rastyazhenii pruzhin mogut odnovremenno voznikat' deformacii rastyazheniya i sdviga. Pruzhiny s malymi uglami naklona vitkov k gorizontali (ris. 1.18) pri ih rastyazhenii vdol' osi v otlichie ot sterzhnei ispytyvayut deformacii sdviga.Pri vozdeistvii s siloi F pruzhina udlinyaetsya na velichinu $\Delta \ell=F/k_1$ , pri etom koefficient ee zhestkosti zavisit ot diametra provoloki d, chisla vitkov i diametrov vitka D i okazyvaetsya ravnym

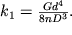
$k_1=\frac{G d^4}{8 n D^3}.$

(1.55a)

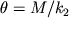
Pri zakruchivanii pruzhiny, podobno valu, vokrug ee osi, kogda k torcevomu ee secheniyu prikladyvaetsya moment vneshnih sil M, vitki pruzhiny ispytyvayut deformacii rastyazheniya i szhatiya (kak pri izgibe balki). V etom sluchae ugol zakruchivaniya $\theta=M/k_2$ , gde koefficient proporcional'nosti

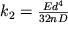
$k_2=\frac{E d^4}{32 n D}$

(1.55b)

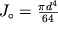
i zavisit ot momenta inercii kruglogo secheniya $J_{\circ}=\frac{\pi d^4}{64}$ (f-la (1.39)), chisla vitkov n i diametra vitka D.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce