Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Ustoichivost' uprugogo ravnovesiya

Znaya uprugie svoistva tel, my vsegda mozhem rasschitat' deformacii pod deistviem zadannyh sil. Takie raschety provodyatsya v kurse teoreticheskoi fiziki, Ih osnovnaya ideya svoditsya k sleduyushemu.

Ris. 1.19.

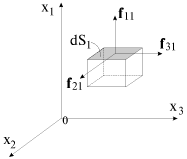
Pod deistviem vneshnih sil v tele sozdayutsya napryazheniya. Eti napryazheniya deistvuyut na elementarnyi ob'em cherez poverhnosti, ego ogranichivayushie. Na ris. 1.19 izobrazhena odna normal'naya f₁₁ i dve tangencial'nye sily f₂₁ i f₃₁, deistvuyushie na zashtrihovannuyu gran' kubika. Moduli etih sil ravny

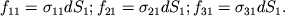
$f_{11}=\sigma_{11}dS_1 ; f_{21}=\sigma_{21}dS_1 ; f_{31}=\sigma_{31}dS_1.$

(1.56)

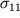
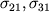
Zdes' indeksy ukazyvayut na to, chto sily prilozheny k ploshadke, perpendikulyarnoi x₁ i deistvuyut v napravlenii osi x₁ ( $\sigma_{11}$ - normal'noe napryazhenie) i osei x₂ i x₃ ( $\sigma_{21},\sigma_{31}$ - sootvetstvuyushie tangencial'nye napryazheniya) Analogichno, no s drugimi indeksami, zapisyvayutsya moduli sil, prilozhennyh k ploshadkam dS₂ i dS₃. Polnaya sila, deistvuyushaya na vydelennyi ob'em, zavisit kak ot orientacii ploshadok, ogranichivayushih etot ob'em, tak i ot vnutrennih napryazhenii v toi oblasti, gde nahoditsya rassmatrivaemyi ob'em. 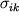Eti napryazheniya opisyvayutsya sovokupnost'yu devyati velichin $\sigma_{ik}$ (i, k=1,2,3), kotorye sostavlyayut tenzor napryazhenii. V uprugih telah deformacii proporcional'ny sootvetstvuyushim napryazheniyam. Takim obrazom, slozhnye deformacii uprugih tel opisyvayutsya sistemoi lineinyh differencial'nyh uravnenii, svyazyvayushih komponenty tenzora deformacii i tenzora napryazhenii. 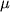Material'nye svoistva sred predstavleny, kak pravilo, koefficientom Puassona $\mu$ (1.4) i modulem vsestoronnego szhatiya k (1.29). Analiz takoi sistemy uravnenii pozvolyaet ne tol'ko rasschitat' deformaciyu tel, no i otvetit' na vopros, ustoichivy li eti deformacii ili net.

Ris. 1.20.

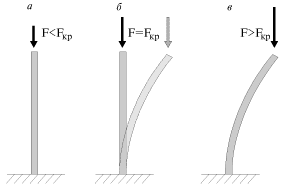
V kachestve primera rassmotrim zadachu o potere ustoichivosti sterzhnya pri ego prodol'nom szhatii siloi F (ris. 1.20). Pri malyh szhimayushih silah szhatiya stoika nahoditsya v ustoichivom ravnovesii, t.k., ispytav maloe sluchainoe otklonenie ot vertikali, stoika, tem ne menee, vozvrashaetsya v vertikal'noe polozhenie. S uvelicheniem nagruzki sluchainye otkloneniya ischezayut vse medlennee so vremenem. Pri F=F_kr nastupaet sostoyanie bezrazlichnogo ravnovesiya: pryamolineinaya forma teryaet ustoichivost', a ustoichivym uzhe budet izognutoe sostoyanie sterzhnya (punktir na ris. 1.20 b). Takoe razdvoenie ravnovesiya, harakterizuyushegosya dvumya ego formami, nazyvaetsya bifurkaciei. Novaya krivolineinaya forma ravnovesiya pri F>F_kr hotya i ustoichiva, odnako takaya deformaciya malo priemlema, poskol'ku v stoike voznikayut nedopustimo bol'shie izgiby i napryazheniya. 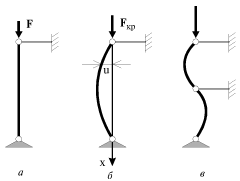Zadacha o vypuchivanii sterzhnya pri prodol'nom szhatii byla reshena v XVIII veke vydayushimsya matematikom Leonardom Eilerom. Rasschitaem, sleduya Eileru, znachenie kriticheskoi sily F_kr i formu izognutogo sterzhnya, kogda poslednii sharnirno zakreplen za oba konca (ris. 1.21).

Ris. 1.21.

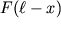
Forma izognutogo sterzhnya u(x) mozhet byt' poluchena iz uravneniya (1.46), v kotorom vmesto momenta poperechnoi sily $F(\ell-x)$ dlya proizvol'nogo secheniya x=const, otmechennogo punktirom, sleduet zapisat' moment sdavlivayushei sily v vide M=Fu. Togda uravnenie (1.46) primet vid:

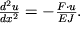
$\frac{d^2 u}{dx^2}=-\frac{F\cdot u}{EJ}.$

(1.57)

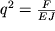
Esli oboznachit' $q^2=\frac{F}{EJ}$ i obratit' vnimanie, chto uravnenie (1.57) analogichno uravneniyu garmonicheskih kolebanii, to ego reshenie zapisyvaetsya srazu v vide

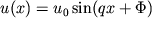
$u(x)=u_0 \sin(qx + \Phi)$

(1.58)

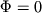
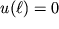
Iz granichnogo usloviya u(0)=0 sleduet, chto $\Phi=0$ . Iz drugogo granichnogo usloviya $u(\ell)=0$ sleduet

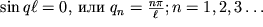
$\sin q\ell=0$, ili $q_n=\frac{n\pi}{\ell}; n=1,2,3\ldots$

(1.59)

Kazhdomu znacheniyu q_n sootvetstvuet svoya konfiguraciya izognutogo sterzhnya, predstavlyayushaya soboi sinusoidu, imeyushuyu n poluvoln. Eti konfiguracii voznikayut pri sootvetstvuyushih znacheniyah sil, ravnyh

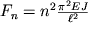
$F_n=n^2\frac{\pi^2 EJ}{\ell^2}$

(1.60)

Pri n=1 formula (1.60) daet znachenie kriticheskoi sily

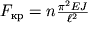
$F_{kr}=n\frac{\pi^2 EJ}{\ell^2}$

(1.61)

Poslednyaya formula byla poluchena Eilerom i nosit ego imya. Drugie napravlennye formy ravnovesiya (n=2, 3...) yavlyayutsya neustoichivymi, odnako oni mogut byt' realizovany, esli sterzhen' dopolnitel'no zakrepit' sharnirnymi oporami v secheniyah, gde u=0 (ris.1.21v). Poluchennyi rezul'tat imeet bol'shoe prakticheskoe znachenie. V silu neustoichivosti sterzhnei pri ih szhatii, tolkayushie rychagi i shtoki v mashinah delayut po vozmozhnosti koroche i bol'shogo secheniya, v to vremya kak tyanushie shtoki, imeyushie bol'shoi zapas prochnosti na razryv, mogut byt' i ne ochen' tolstymi. Po analogii legko ponyat', chto germetichnye emkosti, ispytyvayushie nagruzku na razryv (naprimer, parovye kotly) delayut bolee tonkostennymi, chem emkosti, podverzhennye szhatiyu (obolochki batiskafov, podvodnyh lodok i pr.)

Energiya uprugih deformacii

Pri deformacii vneshnie sily sovershayut rabotu. Eta rabota v obshem sluchae idet na uvelichenie potencial'noi energii (nagrevanie tela). Tak, naprimer, esli my budem pytat'sya perelomit' provoloku, to mesto ee mnogokratnogo izgiba mozhet sil'no nagret'sya, prezhde chem provoloka perelomitsya. V real'nyh telah voznikayushie sily vnutrennih napryazhenii zavisyat ne tol'ko ot velichiny deformacii, no i ot ih skorosti. Poetomu rabota protiv takih sil, nazyvaemyh silami "vnutrennego treniya" i idet na nagrevanie tela. S etimi silami i svyazany plasticheskie deformacii, kogda ne vypolnyaetsya zakon Guka i sushestvuyut ostatochnye deformacii pri prekrashenii vneshnego vozdeistviya.

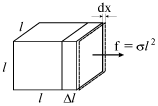Ris. 1.22.

Poschitaem rabotu, zatrachivaemuyu na maluyu deformaciyu elementa ob'ema tela. Pri rastyazhenii predvaritel'no uzhe deformirovannogo kubika (ris.1.22) na velichinu dx elementarnaya rabota

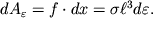
$dA_\varepsilon =f\cdot dx = \sigma\ell^3 d\varepsilon.$

(1.62)

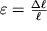
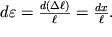
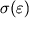
V (1.62) uchteno, chto $\varepsilon=\frac{\Delta \ell}{\ell}$ , a $d\varepsilon=\frac{d(\Delta\ell)}{\ell}=\frac{dx}{\ell}.$ Poskol'ku, kak sleduet iz ris. 1.7, $\sigma(\varepsilon)$ - nelineinaya funkciya deformacii, to polnaya rabota, zatrachivaemaya na privedenie tela v deformacionnoe sostoyanie, ravna

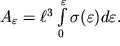
$A_\varepsilon= \ell^3 \int\limits_0^{\varepsilon} \sigma(\varepsilon) d\varepsilon.$

(1.63)

Po analogii, rabota pri sdvige zadaetsya integralom vida:

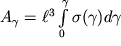
$A_\gamma= \ell^3 \int\limits_0^{\gamma} \sigma(\gamma) d\gamma$

(1.64)

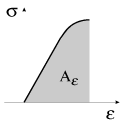Ris. 1.23.

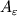
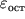
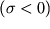
Na diagramme (1.23) rabota $A_\varepsilon$ ravna chislenno zashtrihovannoi ploshadi. Opyt, odnako, pokazyvaet, chto esli deformacii vyidut za oblast' uprugosti, to pri snyatii vneshnih nagruzok v tele budut sushestvovat' ostatochnye deformacii $\varepsilon_{ost}$ (ris. 1.24). Chtoby ih ustranit', nado prilozhit' szhimayushuyu silu $(\sigma<0)$ . Takoe neodnoznachnoe povedenie deformacii v zavisimosti ot prilozhennyh napryazhenii nosit nazvanie uprugogo gisterezisa. 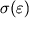Pri periodicheski povtoryayushihsya deformaciyah diagramma $\sigma(\varepsilon)$ izobrazitsya zamknutoi krivoi, kotoraya nazyvaetsya petlei gisterezisa. Ploshad' etoi petli, ochevidno, v sootvetstvii s zakonom sohraneniya energii, ravna kolichestvu tepla, idushego na nagrevanie tela. 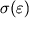Kogda deformacii ne vyhodyat za predely lineinogo uchastka $\sigma(\varepsilon)$ , gisterezis otsutstvuet. 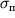Na praktike detali mehanizmov, ispytyvayushie mnogokratnye, periodicheski povtoryayushiesya deformacii, delayut iz materialov s bol'shoi velichinoi predela proporcional'nosti $\sigma_p$ . 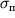Tak, naprimer, dlya zakalennoi pruzhinnoi stali, etot predel, kak vidno iz tablicy, imeet ochen' vysokuyu velichinu: $\sigma_p$ =7500 kg/sm² .Po etoi prichine, naprimer, pruzhiny klapanov dvigatelei delayut iz zakalennoi stali.

Ris. 1.24.

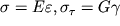
Na lineinom uchastke, gde $\sigma=E \varepsilon , \sigma_\tau=G\gamma$ , integraly (1.63) i (1.64) legko vychislyayutsya:

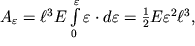
$A_\varepsilon=\ell^3 E \int\limits_0^\varepsilon \varepsilon \cdot d\varepsilon= \frac{1}{2} E \varepsilon^2 \ell^3,$

(1.65)

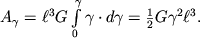
$A_\gamma=\ell^3 G \int\limits_0^\gamma \gamma \cdot d\gamma= \frac{1}{2} G \gamma^2 \ell^3.$

(1.66)

V etom sluchae rabota zatrachivaetsya tol'ko na uvelichenie potencial'noi energii uprugoi deformacii. V edinice ob'ema deformirovannogo tela zapasaetsya energiya

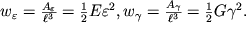
$w_\varepsilon=\frac{A_\varepsilon}{\ell^3}=\frac{1}{2} E \varepsilon^2, w_\gamma=\frac{A_\gamma}{\ell^3}=\frac{1}{2} G \gamma^2.$

(1.67)

Velichiny i nosyat nazvanie ob'emnyh plotnostei energii deformacii rastyazheniya i sdviga sootvetstvenno. Oni igrayut opredelennuyu rol' pri podschete kolichestva energii, perenosimoi akusticheskoi volnoi v sploshnyh sredah.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce