Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Lekciya 2

Zhidkost' i gaz v sostoyanii ravnovesiya. Usloviya ravnovesiya. Raspredelenie davlenii v zhidkosti, nahodyasheisya vo vneshnem pole. Plavanie tel. Raspredelenie plotnosti i davleniya v atmosfere. Vozduhoplavanie. Centrifugirovanie. Pod deistviem vneshnih sil v zhidkosti i gazah, kak i v tverdyh telah, mogut voznikat' vnutrennie napryazheniya. Rassmatrivaya ih kak sploshnye sredy, my otmetim, chto zhidkosti, ne imeya opredelennoi formy, sohranyayut prakticheski neizmennym svoi ob'em. Gazy zhe ne imeyut ni opredelennoi formy, ni fiksirovannogo ob'ema. V zhidkosti (dalee etot termin budet ispol'zovat'sya i dlya gazov, za isklyucheniem tol'ko otdel'no ogovarivaemyh sluchaev) sily scepleniya mezhdu molekulami maly, i zhidkost' ne okazyvaet soprotivleniya rastyazheniyu Odnako pri szhatii sily ottalkivaniya mezhdu molekulami mogut byt' ves'ma znachitel'nymi. Po etoi prichine govoryat ne o rastyagivayushih napryazheniyah $\sigma_{ij}$ , a o davleniyah $p_{ij} = - \sigma_{ij}$ , kak ob otricatel'nyh (szhimayushih) napryazheniyah. Sovokupnost' davlenii p_ij, deistvuyushih na ploshadki, ogranichivayushie element zhidkosti, nazyvaetsya tenzorom davlenii. Opyt pokazyvaet, chto v pokoyasheisya ili medlenno dvizhusheisya zhidkosti tangencial'nye davleniya p_ij (i\ne j), svyazannye s vyazkost'yu zhidkosti, otsutstvuyut. V etom mozhno ubedit'sya, zastaviv, naprimer, massivnoe telo, plavayushee na poverhnosti zhidkosti, peremeshat'sya vdol' poverhnosti pod deistviem skol' ugodno maloi sily. V etoi situacii kasatel'nye napryazheniya, peredavaemye ot verhnego (uvlekaemogo telom) sloya k nizhnim sloyam zhidkosti, prenebrezhimo maly.

Zakon Paskalya.

Esli prenebrech' vnachale silami tyagoteniya, deistvuyushimi na kazhduyu chasticu zhidkosti (ili silami inercii, esli takovye sushestvuyut), to iz prosteishih soobrazhenii otnositel'no uslovii ravnovesiya elementa zhidkosti sleduet, chto

p₁₁ = p₂₂ = p₃₃ = p,

(2.1)

pri etom davlenie p, yavlyayusheesya skalyarnoi velichinoi, odinakovo vo vseh tochkah ob'ema, zanyatogo pokoyasheisya zhidkost'yu. Uslovie (2.1) avtomaticheski obespechivaet ne tol'ko ravenstvo nulyu summy sil davleniya, prilozhennyh k dannomu elementu, no ravenstvo nulyu summarnogo momenta etih sil. Dlya ego dokazatel'stva rassmotrim nepodvizhnuyu zhidkost', pomeshennuyu v cilindricheskii sosud secheniem S₁, zakrytyi sverhu porshnem (ris. 2.1, levyi sosud). Esli nadavit' na porshen' s siloi F₁, to v zhidkosti budut sozdany vnutrennie napryazheniya (davleniya). Na edinicu poverhnosti elementa zhidkosti budet deistvovat' szhimayushaya sila f_ii = - p_iin_i, napravlennoe protivopolozhno vneshnei normali n_i k i-oi poverhnosti (na ris. 2.1 izobrazheny tol'ko dve sily).

Ris. 2.1.

Poskol'ku sily, deistvuyushie na protivopolozhnye grani kubika, ravny po velichine, to p₁₁=F₁/S₁. Ravenstvo davlenii p₁₁ i r₂₂ sleduet iz usloviya ravnovesiya poloviny kubika, vydelennogo bolee temnym cvetom i izobrazhennogo na fragmente. Deistvitel'no, f₁₁=f₂₂=f/ $\sqrt{2}$ , poetomu r₂₂=r₁₁. Rassmatrivaya ravnovesie elementarnyh ob'emov v razlichnyh tochkah zhidkosti, poluchim uslovie:

$p_{ii} = p = \frac{F_1}{S_1},$

(2.2)

kotoroe i yavlyaetsya matematicheskim vyrazheniem zakona Paskalya. Esli etot sosud soedinit' pri pomoshi trubki s drugim cilindricheskim sosudom secheniem S₂, to pri otkryvanii krana K vnutrennie napryazheniya po zhidkosti, nahodyasheisya v soedinitel'noi trubke, v sootvetstvii s zakonom Paskalya peredadutsya vo vtoroi sosud (ris. 2.1). Na porshen', ego zakryvayushii, zhidkost' budet davit' vverh s siloi

$F_2 = pS_2 = \frac{F_1}{S_1}S_2.$

(2.3)

Esli S₂>S₁, to razvivaemoe usilie F₂>F₁. Etot vyigrysh v sile ispol'zuetsya vo mnogih gidroprivodyashih ustroistvah (gidroprivodah): v privode kovsha ekskavatora, rulei raket i samoletov. Na etom zhe principe rabotaet gidravlicheskii press, gidravlicheskii domkrat i t.d. V sisteme SI za edinicu davleniya prinimaetsya Paskal' (Pa), pri etom 1Pa=1N/1m². V tehnike v kachestve edinicy davleniya ispol'zuetsya tehnicheskaya atmosfera: 1at=1kGs/1sm²=9,8*10⁴ Pa.

Zhidkost' vo vneshnem pole.

Rassmotrim napryazheniya, voznikayushie v zhidkosti, nahodyasheisya v pole tyazhesti ili v pole sil inercii, kogda sosud s zhidkost'yu mozhet dvigat'sya s uskoreniem. Pust' k kubicheskomu elementu zhidkosti ob'emom dV=dxdydz prilozhena vneshnyaya sila FdV (F - sila, prilozhennaya k edinice ob'ema zhidkosti, (ris. 2.2). V rezul'tate voznikayushih vnutrennih napryazhenii na nizhnyuyu gran' kubika s koordinatoi x i ploshad'yu dy*dz v polozhitel'nom napravlenii osi x deistvuet sila davleniya velichinoi p(x,y,z)dydz, a na verhnyuyu gran' - p(x+dx,y,z)dydz. Pri ravnovesii kubika, ochevidno, neobhodimo, chtoby

Ris. 2.2.

p(x,y,z)dydz - p(x+dx,y,z)dydz + F_xdxdydz = 0

(2.4a)

Analogichnye po smyslu ravenstva dolzhny byt' zapisany i po dvum ostavshimsya osyam koordinat:

p(x,y,z)dxdz - p(x,y+dy,z)dxdz + F_ydxdydz = 0

(2.4b)

p(x,y,z)dxdy - p(x,y,z+dz)dxdy + F_zdxdydz = 0

(2.4v)

Razdeliv levye i pravye chasti zapisannyh vyshe ravenstv na ob'em elementa, poluchaem usloviya ravnovesiya v vide differencial'nyh uravnenii

$- \frac{\partial p}{\partial x} + F_x = 0; - \frac{\partial p}{\partial y} + F_y = 0; - \frac{\partial p}{\partial z} + F_z = 0.$

(2.5)

Uravneniya (2.5) pokazyvayut, chto davlenie ne ostaetsya postoyannym i izmenyaetsya v teh napravleniyah, po kotorym deistvuet vneshnyaya sila. Esli vvesti vektor gradienta davleniya

${\rm grad} p = \nabla p = \frac{\partial p}{\partial x}e_x + \frac{\partial p}{\partial y}e_y + \frac{\partial p}{\partial z}e_z,$

(2.6)

gde e_x, e_y i e_z - edinichnye vektory vdol' osei koordinat, to uravneniya (2.5) zapishutsya v bolee kompaktnom vektornom vide

-grad p + F = 0

(2.7)

V sootvetstvii so smyslom vvedennogo v predydushih lekciyah vektora gradienta skalyarnoi velichiny iz (2.7) sleduet, chto davlenie naibolee bystro narastaet v napravlenii deistviya vneshnei sily F, a v perpendikulyarnyh napravleniyah ostaetsya postoyannym. Takim obrazom, mozhno govorit' o poverhnostyah ravnogo davleniya, normal' k kotorym v kazhdoi tochke sovpadaet s napravleniem prilozhennoi v etoi tochke vneshnei sily. Neslozhno rasschitat' raspredelenie davlenii po ob'emu zhidkosti, esli prinyat' vo vnimanie, chto komponenty vneshnei sily F vyrazhayutsya cherez proizvodnye poka neizvestnoi skalyarnoi funkcii koordinat p(x,y,z). Eto oznachaet, chto sila F dolzhna byt' potencial'noi i, sledovatel'no, mozhet byt' vyrazhena cherez potencial'nuyu funkciyu U (potencial'nuyu energiyu edinicy ob'ema zhidkosti vo vneshnem pole) sleduyushim obrazom:

F = -grad U

(2.8)

Podstaviv (2.8) v (2.7), poluchim

grad (p + U) = 0, ili p + U = const.

(2.7)

Konstanta v (2.9) opredelyaetsya iz usloviya normirovki potenciala i davleniya.

Zhidkost' v pole sily tyazhesti.

Pust' neszhimaemaya zhidkost' (naprimer, voda) nahoditsya v pole tyazhesti $F = \rho g$ , pri etom $\rho = {\rm const}$ . Dlya rascheta raspredeleniya davlenii udobno napravit' os' x vdol' sily tyazhesti, sovmestiv ee nachalo so svobodnoi poverhnost'yu zhidkosti. Poskol'ku potencial'nuyu funkciyu mozhno zapisat' v vide $U(x) = -\rho gx$ (normirovka potenciala takova, chto U(0)=0), to raspredelenie davlenii po glubine opredelyaetsya iz sootnosheniya

$p(x) - \rho gx = {\rm const}$

(2.10)

Konstanta C opredelyaetsya iz usloviya ravenstva davleniya na poverhnosti vody atmosfernomu davleniyu p₀. Sledovatel'no,

$p(x) = p_0 + \rho gx.$

(2.11)

Esli prinyat' atmosfernoe davlenie $p_0 \approx 10^5$ Pa, plotnost' vody $\rho = 10^3$ kg/m³, to iz (2.11) legko poschitat', chto s uvelicheniem glubiny na kazhdye 10 metrov ( $\Delta x$ =10 m) davlenie uvelichivaetsya na velichinu atmosfernogo davleniya ( $\Delta p = p_0$ ). Vazhno otmetit', chto vozrastanie davleniya s glubinoi ne zavisit ot formy sosuda, v kotoryi nalita zhidkost'. Yarkoi illyustraciei spravedlivosti etogo utverzhdeniya yavlyaetsya odinakovost' urovnei zhidkosti v dvuh soobshayushihsya sosudah proizvol'noi formy (ris. 2.3). Deistvitel'no, ravenstvo dvuh gorizontal'nyh sil davleniya, obespechivayushih ravnovesie kubika zhidkosti v nizhnei chasti soobshayushihsya sosudov vozmozhno lish' pri ravenstve vysot stolbov vody v oboih sosudah.

Ris. 2.3.

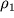
Proillyustriruem neskol'ko eksperimentov s soobshayushimisya sosudami. Pust' oba kolena U-obraznogo sosuda (ris. 2.4) razdeleny podvizhnoi peregorodkoi P, pri etom pravoe koleno zapolneno vodoi, a levoe - rtut'yu, plotnost' kotoroi $\rho_1$ bolee chem v 10 raz prevyshaet plotnost' vody $\rho$ ( $\rho_1 = 13,6\rho$ ). Ochevidno, ravnovesie v etoi situacii dostigaetsya pri vysote stolba rtuti $h_1 = \frac{\rho}{\rho_1}h$ , znachitel'no men'shei vysoty stolba vody h. Umestno pomnit', chto stolb rtuti vysotoi h₁=760 mm uravnoveshivaet davlenie 10-metrovogo stolba vody, ili pochti 10-kilometrovogo stolba atmosfery. Poetomu dlya izmereniya atmosfernogo davleniya ispol'zuyut rtutnye manometry, a atmosfernoe davlenie izmeryayut v millimetrah rtutnogo stolba. Takoi manometr predstavlyaet soboi dva soobshayushihsya sosuda, zapolnennyh rtut'yu. Odin iz sosudov v vide tonkoi trubki zapolnen sverhu i iz nego udalen vozduh, a vtoroi soobshaetsya s atmosferoi (ris. 2.5).

Ris. 2.4.

Ris. 2.5.

Esli izmeryaemye davleniya na 1-2 poryadka men'she atmosfernogo davleniya, to mozhno ispol'zovat' i vodyanye manometry (sm. Posleduyushie lekcii). Zavershaya opisanie ravnovesiya zhidkosti, otmetim, chto v Mirovom okeane iz-za bol'shih glubin formula (2.11) nuzhdaetsya v utochnenii, t.k. plotnost' uvelichivaetsya s glubinoi. Za isklyucheniem neskol'kih neobychnyh mest ona mozhet menyat'sya ot geograficheskogo polozheniya v predelah 2% ot postoyannoi velichiny $\rho$ = 1035 kg/m3. Obychno kolebaniya plotnosti obuslovleny kolebaniyami temperatury i solenosti vody.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce