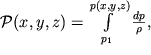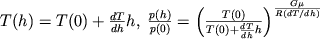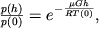Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Ravnovesie szhimaemoi zhidkosti.

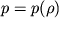
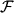
Pri vnutrennih napryazheniyah plotnost' gazov ne ostaetsya postoyannoi. Mozhno schitat', chto davlenie yavlyaetsya funkciei plotnosti ( $p=p(\rho)$ ), prichem vid etoi funkcii, kak budet pokazano nizhe, zadaetsya usloviyami, pri kotoryh nahoditsya gaz. Poetomu v mehanike sploshnyh sred v etih sluchayah operiruyut s plotnost'yu sily ${\cal F}$ , to est' s siloi, prilozhennoi k edinice massy, kotoraya svyazana s siloi F v (2.7) sootnosheniem

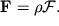
${\bf F}=\rho {\cal F}.$

(2.21)

Togda uslovie ravnovesiya (2.7) primet vid

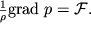
$\frac{1}{\rho}{\rm grad}\; p={\cal F}.$

(2.22)

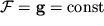
V levuyu chast' etogo ravenstva vhodyat davlenie i plotnost', yavlyayushiesya neizvestnymi funkciyami koordinat, a pravaya chast' obychno izvestna. V pole sily tyazhesti ${\cal F}={\bf g}={\bf {\rm const}}$ . V etom sluchae poverhnostyami ravnyh davlenii i plotnostei budut gorizontal'nye ploskosti, dve iz kotoryh p(x₁) = p₁ i p(x) = p izobrazheny na ris. 2.15. Esli my vvedem vspomogatel'nuyu funkciyu

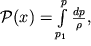
${\cal P}(x)=\int\limits_{p_1}^{p}\frac{dp}{\rho},$

(2.23)

to (2.22) mozhet byt' perepisano v vide, analogichnom (2.7):

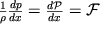
$\frac{1}{\rho}\frac{dp}{dx}=\frac{d{\cal P}}{dx}={\cal F}$

(2.24)

Vvodya dalee dlya edinicy massy potencial'nuyu energiyu U₁, s kotoroi vneshnyaya sila svyazana sootnosheniem

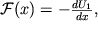
${\cal F}(x)=-\frac{dU_1}{dx},$

(2.25)

poluchaem uravnenie, analogichnoe (2.9):

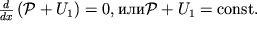
$\frac{d}{dx}\left( {\cal P} + U_1 \right) =0, ili {\cal P} +U_1 = {\rm const}.$

(2.26)

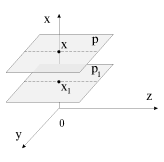Ris. 2.15.

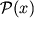
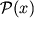
Zamechanie. Vspomogatel'naya funkciya ${\cal P}(x)$ zavisit ot verhnego predela p integrala (2.23), vychislenie kotorogo vozmozhno pri izvestnoi svyazi mezhdu davleniem i plotnost'yu. S drugoi storony, esli naiti zavisimost' ${\cal P}(x)$ (s pomosh'yu (2.24) ili (2.26)), to mozhno opredelit' funkciyu p(x) v (2.23), chto pozvolyaet poluchit' raspredelenie davlenii. 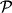Ochevidno, chto poverhnosti ravnogo znacheniya velichiny ${\cal P}$ sovpadayut s poverhnostyami ravnogo davleniya. V zadachah s trehmernym raspredeleniem davleniya i plotnosti vspomogatel'naya funkciya

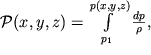
${\cal P}(x,y,z)=\int\limits_{p_1}^{p(x,y,z)}\frac{dp}{\rho},$

(2.27)

a uslovie ravnovesiya imeet vid

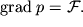
${\rm grad}\; p={\cal F}.$

(2.28)

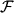
Poskol'ku sila ${\cal F}$ svyazana s potencial'noi energiei edinicy massy sootnosheniem

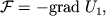
${\cal F}=-{\rm grad}\; U_1,$

(2.29)

to podstanovka (2.29) v (2.28) daet uslovie

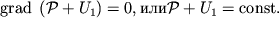
${\rm grad}\; \left( {\cal P} + U_1\right) =0, ili {\cal P} + U_1={\rm const}.$

(2.30)

Sleduet otmetit', chto uslovie ravnovesiya (2.28) yavlyaetsya bolee obshim, chem (2.7), t.k. pozvolyaet rasschitat' raspredelenie davlenii kak v zhidkostyah, tak i v gazah.

Atmosfera v pole sily tyazhesti.

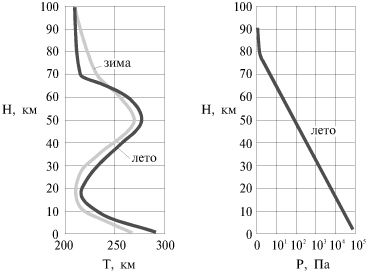
Mnogochislennye issledovaniya atmosfery, provedennye pri pomoshi aerostatov (sm. nizhe), raket i iskusstvennyh sputnikov Zemli, pokazyvayut, chto po mere uvelicheniya vysoty davlenie i plotnost' monotonno ubyvayut, a temperatura monotonno ubyvaet lish' v nizhnem 10-kilometrovom sloe, a v bolee vysokih sloyah menyaetsya nemonotonno. Parametry atmosfery zavisyat kak ot geograficheskogo polozheniya mesta, tak i ot vremeni goda. V kachestve illyustracii k skazannomu na ris. 2.16 predstavleny vysotnye zavisimosti parametrov srednestatisticheskoi atmosfery Moskvy, poluchennye v letnee i zimnee vremya. Esli raznica v vysotnyh zavisimostyah temperatury atmosfery sostavlyaet desyatki gradusov, to raspredelenie "zimnego" davleniya otlichaetsya ot "letnego" vsego lish' na neskol'ko procentov, i na risunke eta raznica nerazlichima. Slozhnaya vysotnaya zavisimost' temperatury atmosfery est' rezul'tat sovmestnogo proyavleniya processov teplomassoperenosa, iniciiruemyh izlucheniem Solnca. Raschety pokazyvayut, chto esli by atmosfera i Mirovoi okean, nazyvaemye zhidkoi obolochkoi Zemli, ne pogloshali by energiyu solnechnogo izlucheniya, to Zemlya nagrelas' by na ekvatore do 270 K, na Yuzhnom polyuse - do 150 K i na Severnom polyuse - do 170 K. Pri takih temperaturah ustanovilos' by radiacionnoe ravnovesie: nagretaya Zemlya izluchala by v mirovoe prostranstvo stol'ko energii, skol'ko poluchaet ot Solnca. Odnako poverhnost' Zemli znachitel'no teplee, a kontrast temperatur mezhdu ekvatorom i polyusom namnogo men'she. Eto - rezul'tat poglosheniya solnechnoi energii samoi atmosferoi. Krome togo, atmosfera i okean perenosyat teplo ot odnoi oblasti k drugoi, chto takzhe vliyaet na energeticheskii balans. Pogloshenie solnechnoi energii osushestvlyaetsya glavnym obrazom vodyanym parom, uglekislym gazom i ozonom, vsledstvie chego sozdaetsya "parnikovyi effekt", privodyashii k dopolnitel'nomu nagrevaniyu poverhnosti Zemli. Poskol'ku vozduh vblizi poverhnosti bolee teplyi i legkii, chem vozduh sverhu, to on vsplyvaet vverh (vertikal'naya konvekciya), i nizhnii sloi atmosfery peremeshivaetsya. Poetomu raspredelenie temperatury, izobrazhennoe na ris. 2.16, yavlyaetsya rezul'tatom dinamicheskogo ravnovesiya atmosfery v pole sily tyazhesti, pri kotorom soblyudaetsya balans energii. Radiacionnoe ravnovesie mozhno rasschitat', esli prinyat' vo vnimanie, chto v nizhnem sloe atmosfery osnovnym fizicheskim faktorom, otvechayushim za dostizhenie ravnovesiya, yavlyaetsya pogloshenie radiacii vodyanym parom. Na bol'shih vysotah dominiruyushim yavlyaetsya pogloshenie uglekislym gazom i ozonom.

Ris. 2.16.

Atmosfera delitsya na otdel'nye uchastki, kak eto vidno iz ris. 2.16. Nizhnii sloi atmosfery, nazyvaemyi troposferoi, soderzhit 80% massy atmosfery, pochti ves' vodyanoi par i oblaka i harakterizuetsya sil'nym vertikal'nym peremeshivaniem. Sverhu troposfera ogranichena tropopauzoi, gde temperatura atmosfery menyaetsya ochen' malo. Vyshe raspolozhena stratosfera, kotoraya slabo peremeshivaetsya. Ee ustoichivost' obuslovlivaetsya povysheniem temperatury s vysotoi v rezul'tate radiacionnogo balansa. Vozrastanie temperatury zakanchivaetsya v stratopauze. Vyshe nahoditsya mezosfera, gde temperatura opyat' padaet. Mezosfera soderzhit lish' 0,1% massy vsei atmosfery. Vyshe mezosfery (H>100 km) nahoditsya termosfera, v kotoroi temperatura opyat' rastet s vysotoi, dostigaya 600 K v period spokoinogo Solnca i bolee 2000 K v period solnechnoi aktivnosti. Dlya vychisleniya izmeneniya atmosfernogo davleniya s vysotoi vospol'zuemsya usloviem ravnovesiya (2.24) v vide:

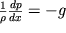
$\frac{1}{\rho}\frac{dp}{dx}=-g$

(2.31)

Svyaz' mezhdu davleniem i plotnost'yu dlya suhogo vozduha zadaetsya uravneniem sostoyaniya ideal'nogo gaza

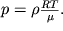
$p=\rho \frac{RT}{\mu}.$

(2.31)

Spravedlivost' ispol'zovaniya etogo uravneniya obuslovlena tem, chto vliyanie vlazhnosti na plotnost' vozduha sushestvenno lish' v tropikah vblizi poverhnosti Zemli, odnako dazhe zdes' oshibka pri ispol'zovanii (2.32) ne prevoshodit 2%. Podstavlyaya znachenie plotnosti $\rho$ iz (2.32) v (2.31), poluchaem uravnenie

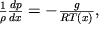
$\frac{1}{\rho}\frac{dp}{dx}=-\frac{g}{RT(x)},$

(2.33)

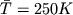
kotoroe mozhno prointegrirovat', esli izvestna T(x). V kachestve grubogo priblizheniya v (2.33) mozhno ispol'zovat' srednee znachenie temperatury ${\bar T} = 250 K$ , pri etom otklonenie maksimal'noi temperatury u poverhnosti ili minimal'noi temperatury na vysote H = 100 km ot srednego znacheniya sostavlyayut okolo 15%. Integriruya (2.33), poluchaem raspredelenie davleniya izotermicheskoi atmosfery

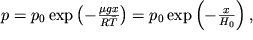
$p=p_0\exp\left(-\frac{\mu gx}{R{\bar T}}\right)=p_0\exp\left(-\frac{x}{H_0}\right),$

(2.34)

nosyashee nazvanie barometricheskoi formuly. Vysota H₀, na kotoroi davlenie padaet v e raz, nazyvaetsya privedennoi vysotoi atmosfery i ravna:

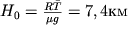
$H_0 = \frac{R{\bar T}}{\mu g} = 7,4 km$

(2.35)

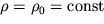
Otmetim, chto esli by plotnost' ne menyalas' s vysotoi ( $\rho = \rho_0 ={\rm const}$ ), to integrirovanie (2.31) privelo by k lineinomu (kak dlya neszhimaemoi zhidkosti) zakonu ubyvaniya davleniya s vysotoi:

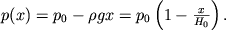
$p(x)=p_0-\rho gx=p_0\left(1-\frac{x}{H_0}\right).$

(2.36)

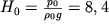
V etom sluchae vsya atmosfera byla by ogranichena vysotoi $H_0=\frac{p_0}{\rho_0 g}=8,4$ km, chto, konechno, protivorechit real'noi situacii. Dlya prakticheskih celei ispol'zuyutsya unificirovannye atmosfernye parametry i ih vysotnye zavisimosti. Tak, Mezhdunarodnaya organizaciya grazhdanskoi aviacii (MOGA) dlya nuzhd aviacii opredelila v 1952 g. standartnuyu atmosferu do vysoty 20 km, a v 1963 g. dala novoe opredelenie do vysoty 32 km. Standartnaya atmosfera est' uslovnaya atmosfera, dlya kotoroi davlenie i temperatura na urovne morya, gradient temperatury i drugie znacheniya byli vybrany namerenno tak, chtoby poluchit' shematichnuyu model' atmosfery, kotoraya nailuchshim obrazom soglasuetsya so srednimi znacheniyami ee parametrov, nablyudaemymi na srednih shirotah. Eta model', v chastnosti, shiroko ispol'zuetsya dlya graduirovaniya al'timetrov (priborov dlya opredeleniya vysoty letatel'nogo apparata). V etoi modeli prinimaetsya, chto do vysoty h = 11000 standartnyh geopotencial'nyh metrov nad urovnem morya, gde temperatura vozduha ravna -56,5 ${}^\circ$ S, gradient temperatury dT/dh raven -0,0065 ${}^\circ$ S na standartnyi geopotencial'nyi metr. Do vysoty 20000 standartnyh geopotencial'nyh metrov dT/dh=0, a vyshe, vplot' do 32000 standartnyh geopotencial'nyh metrov, gradient temperatury raven +0,001 ${}^\circ$ S na standartnyi geopotencial'nyi metr. Geopotencial'nyi metr yavlyaetsya edinicei izmereniya geopotenciala, opredelyaemogo uravneniem

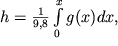
$h=\frac{1}{9,8}\int\limits_{0}^{x}g(x)dx,$

(2.37)

gde uskorenie svobodnogo padeniya

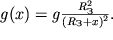
$g(x)=g\frac{R_Z^2}{(R_Z + x)^2}.$

(2.38)

Zdes' R_Z - radius Zemli, g - uskorenie svobodnogo padeniya na srednem urovne morya, x - vysota nad urovnem morya. Esli by uskorenie g ne menyalos' s vysotoi, to vysota h v geopotencial'nyh metrah byla by ravna geometricheskoi vysote nad urovnem morya x. V modeli standartnoi atmosfery sootnosheniya mezhdu davleniem p, temperaturoi T, plotnost'yu $\rho$ i geopotencialom h zadayutsya sleduyushim obrazom:

V dvuh atmosfernyh sloyah s postoyannym gradientom temperatur
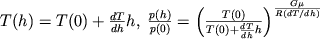
$T(h)=T(0)+\frac{dT}{dh}h,\; \frac{p(h)}{p(0)}=\left(\frac{T(0)}{T(0) + \frac{dT}{dh}h}\right)^{\frac{G\mu}{R(dT/dh)}}$ (2.39)
V izotermicheskom atmosfernom sloe, gde dT/dh = 0 i T(0) = const,
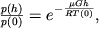
$\frac{p(h)}{p(0)}=e^{-\frac{\mu Gh}{RT(0)}},$ (2.40)

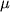
i rabotaet barometricheskaya formula. Zdes' p(0) i T(0) - davlenie i temperatura u osnovaniya kazhdogo sloya, R - universal'naya gazovaya postoyannaya dlya suhogo vozduha, h - raznica geopotenciala mezhdu rassmatrivaemoi tochkoi sloya i ego osnovaniem, $\mu$ - molekulyarnaya massa suhogo vozduha, koefficient G = 9,80665, esli geopotencial vyrazhen v geopotencial'nyh metrah. Uchet izmeneniya temperatury s vysotoi privodit k vysotnoi zavisimosti davleniya (2.39), kotoraya yavlyaetsya luchshei approksimaciei real'noi atmosfery, chem barometricheskaya formula. Dlya bolee glubokogo oznakomleniya s ispol'zovaniem modeli standartnoi atmosfery dlya prakticheskih celei vozduhoplavaniya i dr. rekomenduem chitatelyu obratit'sya k mezhdunarodnym meteorologicheskim tablicam.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce