Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Lekciya 3

Stacionarnoe techenie zhidkosti. Uravnenie Bernulli i ego sledstviya. Ponyatie o divergencii vektora. Uslovie neszhimaemosti. Uravneniya Eilera. Techenie szhimaemyh gazov. Kriterii neszhimaemosti. Rasprostranenie vozmushenii. Skorost' zvuka. Sverhzvukovye potoki.

Stacionarnoe odnomernoe techenie neszhimaemoi zhidkosti.

Ravnovesie zhidkostei i osobenno gazov, rassmotrennoe v predydushei lekcii, sootvetstvuet ideal'nym vneshnim usloviyam i poetomu na praktike realizuetsya kraine redko. Obychno zhidkosti pri vneshnem vozdeistvii prihodyat v dvizhenie, pri etom davlenie i skorost' ee chastic, voobshe govorya, mogut slozhnym obrazom menyat'sya ot tochki k tochke vnutri ob'ema tekushei zhidkosti. Poyasnim skazannoe primerom. Podklyuchim gorizontal'nuyu steklyannuyu trubku peremennogo secheniya pri pomoshi rezinovogo shlanga k vodoprovodnomu kranu (ris. 3.1). Esli napor vody ostaetsya postoyannym, to techenie vody mozhno schitat' ustanovivshimsya (ili stacionarnym). V etom sluchae massa vody M, protekayushaya v edinicu vremeni cherez secheniya s ploshadyami S₁ i S₂ budet odinakovoi, poetomu imeet mesto ravenstvo

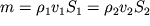$m = \rho_1 v_1 S_1 = \rho_2 v_2 S_2$

(3.1)

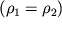
gde ( $\rho$ i v - plotnost' i skorost' zhidkosti v etih secheniyah. Esli zhidkost' neszhimaema $(\rho_1 = \rho_2)$ , to uslovie (3.1) perehodit v uslovie postoyanstva ob'ema zhidkosti (uslovie neszhimaemosti), protekayushego cherez secheniya S₁ i S₂:

V = v₁S₁ = v₂S₂

(3.2)

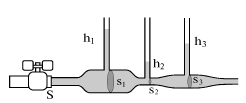Ris. 3.1.

Sleduet otmetit', chto usloviya postoyanstva massy (3.1) i neszhimaemosti zhidkosti (3.2) zapisany dlya sluchaya, kogda skorosti vseh chastic zhidkosti odinakovy v poperechnom sechenii trubki. Dlya graficheskogo izobrazheniya techeniya zhidkosti udobno ispol'zovat' linii toka - linii, kasatel'naya k kotorym v kazhdoi tochke sovpadaet s vektorom skorosti chasticy (ris. 3.2). Legko videt', chto v sechenii S skorosti chastic razlichny, i ob'em protekayushei zhidkosti cherez eto sechenie ne mozhet byt' zapisan v vide (3.2).

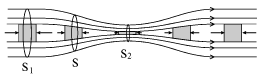Ris. 3.2.

Dalee otmetim, chto po mere priblizheniya k uzkomu secheniyu S₂ chastica, deformiruyas', uskoryaetsya (v silu 3.2), a pri udalenii ot S₂ - zamedlyaetsya. Eti uskoreniya mogut obespechit' lish' sily davleniya f_i = - p_in, pokazannye na ris. 3.2 malen'kimi strelkami. Iz risunka yasno, chto davlenie v zhidkosti po mere priblizheniya k S₂ padaet. A zatem vozrastaet. Eto legko proverit', esli sravnit' urovni h₁ i h₂ zhidkosti v manometricheskih steklyannyh trubkah, vpayannyh v gorizontal'nuyu trubku vblizi sechenii S₁ i S₂. 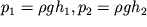Poskol'ku $p_1 = \rho g h_1, p_2 = \rho g h_2$ , to p₁ > p₂, t.k. h₁> ;h₂. Na ris. 3.3 kachestvenno izobrazheno raspredelenie skorostei i davlenii vdol' osi trubki (sm. ris. 3.2).

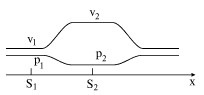Ris. 3.3.

Dlya kolichestvennogo opisaniya techeniya zhidkosti razob'em potok zhidkosti po trube na elementarnye potoki po voobrazhaemym trubkam toka, obrazuemyh semeistvom linii toka. V poperechnom sechenii trubki toka skorost' chastic priblizitel'no odinakova, i eto obstoyatel'stvo sushestvenno oblegchaem analiz techeniya zhidkosti. Naidem kolichestvennuyu svyaz' mezhdu skorost'yu i davleniem, kachestvenno otobrazhennuyu na ris. 3.3. Pri pryamolineinom techenii chastic vody vdol' osevoi trubki toka summa sil, prilozhennyh k edinice ob'ema (sm. 2.5), obespechivayut ego uskorenie. V sootvetstvii so 2-m zakonom N'yutona mozhno zapisat'

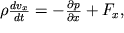$\rho\frac{dv_x}{dt} = -\frac{\partial p}{\partial x} + F_x,$

(3.3)

gde F_x - plotnost', imeyushaya razmernost' N/m³. Otmetim, chto v uravnenie (3.3) ne vhodyat sily vyazkosti, zavisyashie ot skorosti dvizheniya elementa zhidkosti. Vposledstvii my uchtem ih vliyanie i vyyasnim usloviya, pri kotoryh imi mozhno prenebrech'. Izmenenie skorosti chasticy dv_x i svyazannoe s nim uskorenie mozhet proishodit' kak vsledstvie stacionarnogo dvizheniya chasticy ot shirokogo k uzkomu (ili naoborot) secheniyu, tak i pri nestacionarnom izmenenii skorosti techeniya vo vremeni (naprimer, pri medlennom uvelichenii ili oslablenii napora vody s pomosh'yu krana). Poetomu v obshem sluchae skorost' chastic yavlyaetsya funkciei ne tol'ko koordinaty x, no i vremeni t:

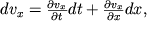$dv_x = \frac{\partial v_x}{\partial t}dt + \frac{\partial v_x}{\partial x}dx,$

(3.4)

gde dx=v_xdt - rasstoyanie, proidennoe chasticei za vremya dt. Podstavlyaya (3.4) v (3.3), prihodim k uravneniyu Eilera

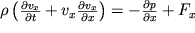$\rho \left( \frac{\partial v_x}{\partial t} + v_x \frac{\partial v_x}{\partial x}\right) = -\frac{\partial p}{\partial x} + F_x$

(3.5)

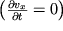
opisyvayushee odnomernoe techenie neszhimaemoi nevyazkoi zhidkosti. Pri stacionarnom techenii zhidkosti po gorizontal'noi trube skorost' ne zavisit ot vremeni $\left( \frac{\partial v_x}{\partial t} =0 \right)$ , vneshnie sily F_x=0, i uravnenie Eilera prinimaet prostoi vid

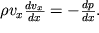
$\rho v_x \frac{dv_x}{dx}=-\frac{dp}{dx}.$

(3.6)

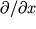
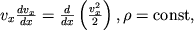
Zdes' vmesto $\partial / \partial x$ ispol'zuetsya simvol polnoi proizvodnoi d/dx. Uchityvaya, chto $v_x \frac{dv_x}{dx}=\frac{d}{dx}\left( \frac{v_x^2}{2} \right), \rho = {\rm const},$ perepishem (3.6) v vide

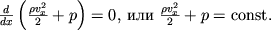
$\frac{d}{dx}\left( \frac{\rho v_x^2}{2} + p \right)=0$, ili $\frac{\rho v_x^2}{2} + p = {\rm const}.$

(3.7)

Ravenstvo (3.7), ustanavlivayushee svyaz' mezhdu davleniem i skorost'yu, yavlyaetsya chastnym sluchaem uravneniya Bernulli. Konstanta, vhodyashaya v eto uravnenie, opredelyaetsya iz znachenii davleniya i skorosti v kakom-libo sechenii trubki toka. Ispol'zuya eto uravnenie, opredelim massu vody (rashod), prohodyashuyu za edinicu vremeni cherez sechenie trubki, izobrazhennoi na ris. 3.2. V sootvetstvii s uravneniem (3.7) davleniya i skorosti v secheniyah S₁ i S₂ svyazany sootnosheniem

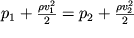
$p_1 + \frac{\rho v_1^2}{2}=p_2 + \frac{\rho v_2^2}{2}$

(3.8)

Pomimo etogo, iskomyi rashod vody opredelyaetsya ravenstvom (3.1):

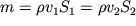
$m=\rho v_1 S_1= \rho v_2 S_2$

(3.9)

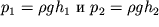
Poskol'ku davlenie $p_1 = \rho g h_1$ i $p_2 = \rho g h_2$ i opredelyayutsya po pokazaniyam h₁ i h₂ manometricheskih trubok, to reshaya sistemu uravnenii (3.8) i (3.9) otnositel'no m, nahodim

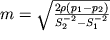
$m=\sqrt{\frac{2\rho (p_1 - p_2)}{S_2^{-2} - S_1^{-2}}}$

(3.10)

Dlya izmereniya rashoda vody na praktike primenyayutsya vodomery, osnovu kotoryh sostavlyaet truba peremennogo secheniya, osnashennaya manometrami dlya izmereniya davlenii p₁ i p₂ v izvestnyh secheniyah S₁ i S₂.

Techenie zhidkosti v pole sily tyazhesti. Uravnenie Bernulli.

Rassmotrim zadachu o techenii zhidkosti vdol' proizvol'nyh trubok toka, mogushih sostavlyat' proizvol'nyi peremennyi ugol s gorizontom. Odna iz nashih krivolineinyh trubok pokazana na ris. 3.4. Esli vvesti krivolineinuyu koordinatu $\ell$ , sovpadayushuyu s os'yu trubki toka, to pri stacionarnom techenii zhidkosti ee skorost' i davlenie yavlyayutsya funkciyami etoi koordinaty. Proektiruya silu tyazhesti na os' $\ell$ , zapishem uravnenie Eilera (3.5) v vide:

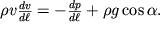
$\rho v \frac{dv}{d\ell}=- \frac{dp}{d\ell}+ \rho g \cos \alpha.$

(3.11)

Zdes' v - skorost' chastic, napravlennaya vdol' osi trubki.

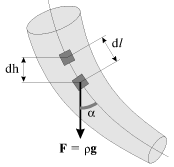Ris. 3.4.

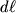
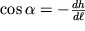
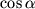
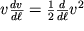
Esli element zhidkosti smestilsya vniz na rasstoyanie $d\ell$ , to on smestilsya (opustilsya) na vysotu dh<0, pri etom $\cos \alpha= - \frac{dh}{d\ell}$ . Podstavlyaya znachenie $\cos \alpha$ v (3.11) i ispol'zuya tozhdestvo $v\frac{dv}{d\ell}=\frac{1}{2}\frac{d}{d\ell}v^2$ , nahodim

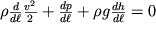
$\rho \frac{d}{d\ell}\frac{v^2}{2}+\frac{dp}{d\ell}+\rho g \frac{dh}{d\ell} =0$

(3.12)

Dlya neszhimaemoi zhidkosti $\rho$ =const, i poslednee ravenstvo transformiruetsya k vidu

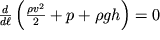
$\frac{d}{d\ell}\left(\frac{\rho v^2}{2} +p + \rho gh \right) =0$

(3.13)

Integriruya (3.13) vdol' trubki toka, poluchaem uravnenie Bernulli

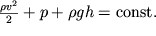
$\frac{\rho v^2}{2}+p+\rho gh = {\rm const}.$

(3.14)

Eto uravnenie opisyvaet stacionarnoe techenie neszhimaemoi zhidkosti (inogda upotreblyayut termin "ideal'noi zhidkosti"), i igraet fundamental'nuyu rol' v gidrodinamicheskih issledovaniyah. Esli nam izvestno davlenie p₁, skorost' v₁ v nekotorom sechenii trubki toka, nahodyashemsya na vysote h₁, to v lyubom drugom sechenii na vysote h velichiny p i v svyazany sootnosheniem

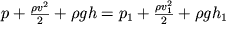
$p+\frac{\rho v^2}{2}+\rho gh = p_1+ \frac{\rho v_1^2}{2}+\rho gh_1$

(3.15)

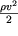
Davlenie p - eto staticheskoe davlenie, kotoroe poluchit manometr, nahodyashiisya v zhidkosti i dvizhushiisya vmeste s neyu, $\frac{\rho v^2}{2}$ - eto dinamicheskoe davlenie, smysl kotorogo budet raskryt pozdnee. Zametim, chto v pokoyasheisya zhidkosti ravenstvo (3.15) opisyvaet gidrostaticheskoe raspredelenie davlenii. Uravnenie Bernulli mozhet byt' polucheno s ispol'zovaniem zakona sohraneniya energii. V otsutstvie sil vyazkosti, prirashenie summarnoi (potencial'noi i kineticheskoi) energii massy vody, nahodyasheisya v trubke toka mezhdu secheniyami S₁ i S₂ (ris. 3.5) ravno rabote sil davleniya. 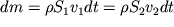Iz risunka vidno, chto za vremya dt techenie zhidkosti ekvivalentno po konechnomu rezul'tatu peremesheniyu elementa massoi $dm=\rho S_1 v_1 dt= \rho S_2 v_2 dt$ s vysoty h₁ na vysotu h₂ i odnovremennomu povysheniyu ego skorosti ot velichiny v₁ do velichiny v₂.

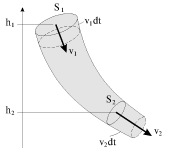Ris. 3.5.

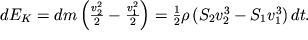
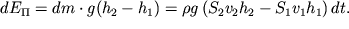
Prirashenie kineticheskoi energii ravno: $dE_K=dm \left(\frac{v_2^2}{2} - \frac{v_1^2}{2}\right)=\frac{1}{2} \rho \left( S_2 v_2^3 -S_1 v_1^3 \right) dt.$ Prirashenie potencial'noi energii $dE_P=dm \cdot g (h_2 - h_1) = \rho g \left( S_2 v_2 h_2 -S_1 v_1 h_1\right) dt.$ Rabota sil davleniya dA=p₁S₁v₁dt - p₂S₂v₂dt. Zapisyvaya uravneniya energeticheskogo balansa v vide dE_K+dE_P=dA, poluchaem uravnenie Bernulli:

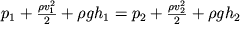
$p_1+\frac{\rho v_1^2}{2}+\rho gh_1 = p_2+ \frac{\rho v_2^2}{2}+\rho gh_2$

(3.16)

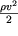
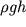
Provedennyi energeticheskii vyvod uravneniya Bernulli delaet bolee ponyatnym fizicheskii smysl vhodyashih v nego chlenov. Tak, staticheskoe davlenie p chislenno ravno rabote sil davleniya, sovershaemyh nad edinichnym ob'emom zhidkosti; dinamicheskoe davlenie $\frac{\rho v^2}{2}$ est' kineticheskaya energiya edinicy ob'ema, a velichina $\rho gh$ yavlyaetsya potencial'noi energiei edinichnogo ob'ema v pole sily tyazhesti. Primenim uravnenie Bernulli k raschetu techeniya zhidkosti v ryade interesnyh fizicheskih zadach.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce