Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Vytekanie zhidkosti cherez otverstie v sosude.

Pust' zhidkost', zapolnyayushaya sosud, pod deistviem sily tyazhesti vytekaet iz nego cherez otverstie v bokovoi stenke, raspolozhennoe vblizi dna sosuda (ris. 3.6). V otverstie vstavlena gorizontal'naya trubka s zakruglennoi vnutrennei kromkoi, napravlyayushaya vytekayushuyu struyu vody. Zakruglennaya kromka obespechivaet polnoe zapolnenie trubki vytekayushei zhidkost'yu.

Ris. 3.6.

Razob'em tekushuyu zhidkost' na trubki toka. Odna iz takih trubok izobrazhena na risunke 3.6. Hotya my i ne znaem, kak vyglyadyat eti trubki, odnako vse oni nachinayutsya na svobodnoi poverhnosti zhidkosti i zakanchivayutsya na vyhodnom torce slivnoi trubki. Esli ploshad' otverstiya trubki S znachitel'no men'she ploshadi svobodnoi poverhnosti S₀, to pri istechenii zhidkosti ee opuskayushayasya s nekotoroi skorost'yu v₀ poverhnost' budet ostavat'sya gorizontal'noi. Eto oznachaet. chto konstanta, vhodyashaya v uravnenie Bernulli (3.14), budet odinakova dlya vseh trubok toka: ${\rm const} = \frac{\rho v_0^2}{2}+p_0+\rho gH.$ Zdes' H - vysota urovnya zhidkosti v sosude. Poetomu skorost' istecheniya zhidkosti v opredelyaetsya iz uravneniya

$\frac{\rho v^2}{2}+ p_0 = \frac{\rho v_0^2}{2}+p_0+\rho gH,$

(3.17)

gde p₀ - atmosfernoe davlenie na svobodnoi poverhnosti i u slivnoi trubki. Poskol'ku S $\ll$ S₀, to iz usloviya neszhimaemosti (3.2) sleduet, chto v₀ $\ll$ v. S uchetom etogo skorost' istecheniya iz (3.17) poluchaetsya ravnoi

$v=\sqrt{2gH}.$

(3.18)

Eta formula nosit nazvanie formuly Torichelli, poskol'ku byla poluchena Torichelli, zhivshem do Bernulli. Srazu brosaetsya v glaza, chto skorost' istecheniya zhidkosti iz sosuda takaya zhe, kak i pri ee svobodnom padenii s vysoty H. V etom net nichego udivitel'nogo, poskol'ku vyazkost'yu my prenebregli, a rabota sil atmosfernogo davleniya nad trubkoi toka ravna nulyu. Poetomu, kak i pri svobodnom padenii tel v otsutstvie soprotivleniya vozduha, pri rashenie kineticheskoi energii ravno rabote sily tyazhesti: $\frac{\rho v^2}{2} = \rho gH.$ Spravedlivost' formuly Torichelli mozhno legko proverit', esli na vyhodnuyu trubku nadet' kusok gibkogo shlanga i vytekayushuyu struyu vody napravit' vverh pod nebol'shim naklonom k vertikali (ris. 3.7). Struya podnimetsya prakticheski do urovnya poverhnosti zhidkosti. Esli zhe struyu napravit' vertikal'no vverh, to vzletayushie vverh chasticy zhidkosti, vzaimodeistvuya s padayushimi vniz chasticami, ne smogut podnyat'sya na vysotu H.

Ris. 3.7.

Interesno otmetit', chto trubki toka zhidkosti raspolozheny preimushestvenno blizhe k stenke sosuda s otverstiem, v to vremya kak u protivopolozhnoi (levoi na ris. 3.8) stenki zhidkost' prakticheski malopodvizhna. Eto oznachaet, chto na levuyu stenku deistvuyut sily davleniya, kotoroe legko poschitat', ispol'zuya lineinyi zakon narastaniya gidrostaticheskogo davleniya s glubinoi, davaemoi formuloi (2.11). Raschet sil davleniya, deistvuyushih na pravuyu stenku, trebuet gidrodinamicheskogo resheniya zadachi. Odnako i bez takogo rascheta yasno, chto v trubke toka, primykayushei k pravoi stenke, davlenie na kazhdoi glubine budet men'she sootvetstvuyushego etoi glubine gidrostaticheskogo davleniya. Eto oznachaet, chto ravnodeistvuyushaya sil davleniya, deistvuyushih na obe stenki, napravlena v storonu, protivopolozhnuyu napravleniyu istecheniya zhidkosti. Pod deistviem etoi sily, nazyvaemoi takzhe reaktivnoi, sosud, postavlennyi na kolesa, mozhet pridti v dvizhenie. Velichinu etoi sily legko poschitat' s ispol'zovaniem formuly Torichelli. Po 3-mu zakonu N'yutona iskomaya reaktivnaya sila ravna po velichine sile, s kotoroi stenki sosuda deistvuyut na vodu, soobshaya ee (po 2-mu zakonu N'yutona) prirashenie impul'sa v napravlenii istecheniya. Poskol'ku massa, vytekayushaya cherez otverstie s secheniem S ravna $\rho v S$ , to izmenenie impul'sa v edinicu vremeni sostavit velichinu $\rho v^2 S.$ Poetomu reaktivnaya sila

$F=\rho v^2 S = 2\rho gHS.$

(3.19)

Ris. 3.8.

Otmetim, chto esli by my oshibochno prinyali, chto raspredelenie davlenii s glubinoi u pravoi stenki bylo takoe zhe, kak u levoi, to reaktivnaya sila poluchilas' by vdvoe men'shei:

$F'=\rho gH\cdot S,$

(3.20)

gde $\rho gH$ - velichina gidrostaticheskogo davleniya na glubine H, S - ploshad' otverstiya v pravoi stenke. Odnako mozhno dobit'sya odinakovogo (gidrostaticheskogo) raspredeleniya davlenii u obeih stenok, esli konec trubki s ostroi kromkoi budet otstoyat' ot pravoi stenki, kak pokazano na ris. 3.9. V etom sluchae reaktivnaya sila mozhet opredelyat'sya s pomosh'yu formuly (3.20). Esli zhe ee vychislyat' pri pomoshi (3.19), to v etoi formule nado vmesto secheniya trubki S podstavit' sechenie strui vody v trubke S_B=kS, gde koefficient istecheniya k $\approx$ 1/2. Pri takom istechenii trubka budet zapolnena zhidkost'yu priblizitel'no napolovinu.

Ris. 3.9.

Reaktivnuyu silu mozhno uvelichit', esli prezhde vsego povysit' skorost' istecheniya zhidkosti. Dlya etogo sleduet ispol'zovat' zamknutyi sosud s otverstiem, pri etom nad svobodnoi poverhnost'yu zhidkosti sozdaetsya davlenie p₁>p₀. Togda skorost' istecheniya zhidkosti iz uravneniya Bernulli poluchaetsya ravnoi:

$v=\sqrt{2\left( gH + \frac{p_1-p_0}{\rho}\right)},$

(3.21)

a reaktivnaya sila vozrastaet lineino s povysheniem izbytochnogo davleniya $\Delta p= p_1 - p_0$ nad svobodnoi poverhnost'yu zhidkosti.

Gidrorezanie.

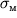
Esli sozdat' ochen' vysokoe izbytochnoe davlenie, naprimer, $\Delta \rho \approx$ 5000 atm = 5*10 N/m2, to skorost' istecheniya vody v = 1000 m/s. Esli takuyu struyu napravit' na kakoi-libo tverdyi material, to ego poverhnost' budet podverzhena gidrodinamicheskomu davleniyu $$p_d=\rho v^2/2$=5000 atm.$ Takoe ogromnoe davlenie v ryade sluchaev mozhet prevoshodit' predel prochnosti $\sigma_m$ nekotoryh materialov, i poslednie budut razrushat'sya pod deistviem strui. So vtoroi poloviny 80-h godov poluchilo razvitie novoe napravlenie v obrabotke materialov - gidrorezanie. V etoi tehnologii vodyanoi nozh - vysoko-skorostnaya struya vody s diametrom igly - legko rezhet materialy tolshinoi v neskol'ko santimetrov so skorost'yu rezaniya neskol'ko desyatkov santimetrov v minutu. Dlya rezki metallov, tverdyh splavov, betona i drugih materialov v struyu dobavlyayut abrazivnyi poroshok. Eto pozvolyaet znachitel'no uvelichit' gidrodinamicheskoe davlenie i povysit' proizvoditel'nost' i vozmozhnosti gidrorezaniya.

Sosud Mariotta.

Ves'ma pouchitel'nym dlya ponimaniya dvizheniya zhidkosti yavlyaetsya istechenie zhidkosti iz sosuda Mariotta. On pozvolyaet obespechit' postoyannuyu skorost' vytekaniya zhidkosti iz sosuda, nesmotrya na ponizheniya ee urovnya. Dlya etogo v sosud cherez germetichnuyu probku v ego gorlovinu vvoditsya trubochka, soobshayushayasya s atmosferoi (ris. 3.10). Skorost' vytekaniya opredelyaetsya po formule Torichelli $v=\sqrt{2gh}$ , gde h - vysota nizhnego konca trubki nad otverstiem. Eto proishodit potomu, chto pri neznachitel'nom istechenii zhidkosti iz polnost'yu zapolnennogo sosuda davlenie pod probkoi budet men'she atmosfernogo, a davlenie v gorizontal'noi ploskosti, sovpadayushei i nizhnim koncom trubki, ravno atmosfernomu. Skorost' vytekaniya legko reguliruetsya vertikal'nym peremesheniem trubki. Esli konec trubki nahoditsya na urovne h=0 ili nizhe otverstiya, to zhidkost' ne vytekaet vovse.

Ris. 3.10.

Uslovie neszhimaemosti dvizhusheisya zhidkosti.

Ravenstvo (3.2), yavlyayusheesya usloviem neszhimaemosti, svyazyvaet skorosti dvizhusheisya zhidkosti v dvuh razlichnyh secheniyah. Mezhdu tem, kak na eto neodnokratno obrashalos' vnimanie v predydushih lekciyah, v fizike vazhno operirovat' s ravenstvami ili uravneniyami, otnesennymi k odnoi tochke prostranstva. Dlya etogo rassmotrim deformaciyu dvizhushegosya kubicheskogo elementa zhidkosti. Esli ego ob'em cherez malyi otrezok vremeni $\delta t$ ne izmenyaetsya, to summa diagonal'nyh elementov tenzora deformacii ravna nulyu, t.e. $\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}=0$ Zdes' u_x, u_y i u_z- smesheniya granei kubika v napravlenii sootvetstvuyushih osei koordinat. Odnako eti smesheniya svyazany so skorostyami dvizheniya granei (a tochnee, chastic zhidkosti, nahodyashihsya v dannyi moment na etih granyah): $u_x=v_x \delta t, u_y=v_y \delta t, u_z=v_z \delta t.$ Podstavlyaya eti ravenstva v (3.22), poluchaem lokal'noe (otnosyasheesya k odnoi tochke prostranstva) uslovie neszhimaemosti v vide

$\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}=0$

(3.22)

V fizike dlya opisaniya vektornyh polei, a v nashem sluchae rech' idet o vektornom pole skorostei v=v(x,y,z,t), ispol'zuetsya ponyatie divergencii (istoka) polya v dannoi tochke prostranstva. V dekartovoi sisteme koordinat vyrazhenie dlya div v imeet vid:

${\rm div }\; {\bf v} = \frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}$

(3.23)

Divergenciya vektora yavlyaetsya skalyarnoi funkciei koordinat i vremeni i legko rasschityvaetsya, esli izvestny komponenty vektornogo polya (v nashem sluchae v_x, v_y i v_z). Poetomu uslovie (3.22) postoyanstva ob'ema neszhimaemoi zhidkosti zapisyvaetsya kratko:

${\rm div }\; {\bf v} = 0.$

(3.24)

Otmetim, chto uravnenie (3.24) yavlyaetsya odnim iz osnovnyh uravnenii gidrodinamiki neszhimaemoi zhidkosti. Sleduet otmetit', chto imeetsya mnozhestvo vektornyh polei, kak, naprimer, elektricheskoe E=E(x,y,z,t) i magnitnoe B=B(x,y,z,t) polya i dr., pri opisanii kotoryh takzhe shiroko ispol'zuetsya ponyatie divergencii: div E ili div B i t.d. Hotya ona opredelyaetsya v sootvetstvii s (3.23), vvoditsya, odnako, neskol'ko iz drugih soobrazhenii, poskol'ku v elektrodinamike ne idet rech' o dvizhenii i deformacii elementa material'noi sredy. Na primere vektornogo polya skorostei v=v(x,y,z,t) poyasnim fundamental'nyi smysl ponyatiya divergencii. Dlya etogo rassmotrim nepodvizhnyi elementarnyi ob'em prostranstva. dV=dxdydx i poschitaem ob'em zhidkosti, vtekayushii i vytekayushii iz etogo ob'ema za edinicu vremeni. Vvedem ponyatie elementarnogo potoka vektora skorosti v cherez malen'kuyu ploshadku dS:

$dN_v = v\cdot dS\cdot \cos\alpha = vdS,$

(3.25)

gde dS=ndS - vektor, napravlennyi po normali n k elementarnoi ploshadke. Yasno, chto potok (3.25) raven ob'emu zhidkosti, peresekayushei ploshadku dS za edinicu vremeni (ris. 3.12). On dopuskaet takzhe naglyadnuyu geometricheskuyu interpretaciyu. V samom dele, v sootvetstvii s opredeleniem linii toka, dannym v nachale etoi lekcii, ih gustota harakterizuet skorost' techeniya. Poetomu velichine skorosti vsegda mozhno postavit' v sootvetstvie kolichestvo linii toka, peresekayushih ploshadku s dS=1 i n || v. Togda potok dN_v v (3.25) budet harakterizovat'sya chislom linii, peresekayushih ploshadku pri ee proizvol'noi orientacii.

Ris. 3.12.

Teper' legko poschitat' balans mezhdu vtekayushei i vytekayushei zhidkost'yu dlya elementarnogo ob'ema, izobrazhennogo na ris. 3.12. Dlya etogo vosstanovim vneshnie normali po vsem 6-ti granyam kubika i poschitaem potoki zhidkosti cherez ego grani. Legko ponyat', chto polozhitel'noe znachenie potoka budet dlya vytekayushei zhidkosti, a otricatel'noe - dlya vtekayushei. Esli skorost' v centre kubika v(x,y,z) izmenyaetsya pri priblizhenii k sootvetstvuyushim granyam, to pri vychislenii takogo potoka eto neobhodimo uchest'. Rezul'tiruyushii potok opredelitsya sleduyushim obrazom:

$dN_v =\left[v_x\left(x + \frac{dx}{2}, y,z,t\right) - v_x\left(x - \frac{dx}{2},y,z,t\right)\right]dydz + \left[v_y\left(x,y + \frac{dy}{2},z,t\right) - v_y\left(x,y - \frac{dy}{2},z,t\right)\right]dxdz + \left[v_z\left(x,y,z + \frac{dz}{2},t\right) - v_z\left(x,y,z - \frac{dz}{2},t\right)\right]dxdy.$

(3.26)

Razdeliv levuyu i pravuyu chasti (3.26) na dxdydz i perehodya k predelu, poluchaem

$\frac{dN_v}{dxdydz} = {\rm div }\; {\bf v}$

(3.27)

Takim obrazom, divergenciya vektora skorosti chislenno ravna potoku zhidkosti cherez poverhnost' edinichnogo ob'ema. Esli zhidkost' neszhimaema, to, estestvenno, etot potok dolzhen byt' raven nulyu. Graficheski poslednee interpretiruetsya kak ravenstvo kolichestva vhodyashih i vyhodyashih linii toka dlya etogo ob'ema. Eto, v svoyu ochered', oznachaet, chto v okrestnosti tochki, gde div v=0, linii toka ne preryvayutsya. Poetomu ravenstvo div v=0 nazyvayut usloviem nerazryvnosti. Iz shkol'nogo kursa fiziki izvestno, chto silovye linii elektrostaticheskogo polya (analog linii toka) preryvayutsya tol'ko na zaryadah. Poetomu dlya oblastei, ne zanyatyh zaryadami, my takzhe vprave napisat' ${\rm div }\; {\bf v} = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y}\frac{\partial E_z}{\partial z} = 0$ . Silovye linii indukcii magnitnogo polya B vsegda zamknuty, poetomu vo vseh sluchayah div B=0.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce