
Mehanika sploshnyh sred
Uravneniya Eilera dlya ideal'noi zhidkosti.
Pri zadannyh vneshnih silah i izvestnyh svoistvah zhidkosti mozhno zapisat', pol'zuyas' 2-m zakonom N'yutona, uravnenie dvizheniya edinicy ob'ema neszhimaemoi nevyazkoi zhidkosti:
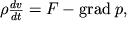
| (3.28) |
gde operator grad (gradient) opredelyaetsya kak
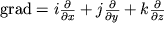
| (3.29) |
Uravnenie (3.28)zapisano v vektornom vide i yavlyaetsya obobsheniem odnomernogo uravneniya (3.3).
Raspisyvaya (3.28) dlya treh proekcii skorosti, poluchaem sistemu uravnenii
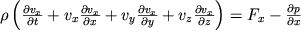
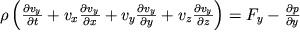
| (3.30) |
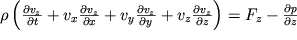
Esli eti uravneniya dopolnit' usloviem nerazryvnosti
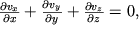
to my poluchaem polnuyu sistemu uravnenii s chetyr'mya neizvestnymi funkciyami koordinat i vremeni (v
x, v
y, v
z i p). Uravneniya (3.29) nazyvayutsya uravneniyami Eilera i pozvolyayut, v principe, rasschitat' dinamiku zhidkosti. Odnako s matematicheskoi tochki zreniya eta sistema, v otlichie ot mnogih drugih uravnenii v fizike, yavlyaetsya nelineinoi iz-za nalichiya chlenov tipa
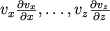
. Poetomu integrirovanie etih uravnenii i nahozhdenie iskomyh funkcii predstavlyaet podchas ves'ma slozhnuyu zadachu dazhe pri ispol'zovanii moshnyh EVM. Neslozhno, naprimer, iz (3.30) poluchit' uravnenie Bernulli dlya stacionarnogo techeniya, kogda
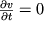
. Odnako strogii vyvod etogo uravneniya my predostavlyaem chitatelyu prodelat' samostoyatel'no, obrativshis' k rekomendovannoi literature. My zhe budem ispol'zovat' uravneniya (3.30) dlya opisaniya volnovogo dvizheniya zhidkosti i analiza svoistv akusticheskih voln.
V zaklyuchenie otmetim, chto chasto sistema (3.30) pishetsya v bolee kompaktnom vide s ispol'zovaniem operatora gradienta. Kazhdoe iz treh uravnenii (3.30) imeet vid
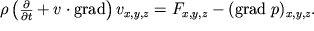
Vozvrashayas' k vektornomu predstavleniyu, poluchaem vozmozhnost' zapisat' 4 uravneniya Eilera (3.29) v vide dvuh vektornyh:
![$\begin{array}{l} \rho\left[\frac{\partial}{\partial t} + v \cdot {\rm grad }\right] v = F - {\rm grad }\; {p}\\ {\rm div }\; {\bf v} = 0. \end{array}$](http://images.astronet.ru/pubd/2002/03/05/0001175083/tex/formula311.gif)
| (3.31) |
Uravnenie nerazryvnosti dlya szhimaemoi zhidkosti
Pri techenii gazov, osobenno pri bol'shih skorostyah, ih plotnost' mozhet zametno, a to i znachitel'no, menyat'sya vo vremeni i v prostranstve. Yasno, chto ob'em vtekayushei zhidkosti mozhet ne byt' ravnym ob'emu vytekayushei zhidkosti cherez poverhnost' kubika, izobrazhennogo na ris. 3.11. Esli takogo ravenstva net, to massa gaza vnutri kubika (a s nei i plotnost') budut so vremenem menyat'sya. Uravnenie (3.24) v etom sluchae stanovitsya nespravedlivym. Odnako i zdes' mozhno zapisat' uravnenie nerazryvnosti, osnovnaya ideya vyvoda kotorogo baziruetsya na balanse massy gaza, sostavlyayushego fizicheskuyu sut' ravenstva (3.1). Potok massy gaza cherez ploshadku d
S budet raven
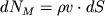
. Togda polnyi potok massy gaza cherez bokovuyu poverhnost' elementa ob'ema dxdydz, analogichno (3.27), raven
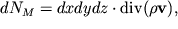
| (3.32) |
gde -
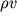
novoe vektornoe pole. Esli etot potok polozhitel'nyi, to massa vnutri elementa
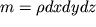
budet ubyvat' za schet umen'sheniya vo vremeni plotnosti . Poetomu, zapisyvaya uslovie balansa massy v vide
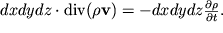
| (3.33) |
my poluchaem (posle sokrasheniya na dxdydz) odno iz fundamental'nyh uravnenii gidrodinamiki - uravnenie nerazryvnosti szhimaemoi zhidkosti:
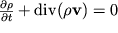
| (3.34) |
Sleduet otmetit', chto pri

=const eto uravnenie perehodit v (3.24).
 |
| Ris. 3.11. |
V elektrodinamike eto uravnenie yavlyaetsya takzhe fundamental'nym. V samom dele, esli rech' idet o dvizhushihsya zaryadah, ob'emnaya plotnost' kotoryh ravna

, to uravnenie (3.34) yavlyaetsya matematicheskim vyrazheniem universal'nogo zakona sohraneniya zaryada.
Uravneniya Eilera i uravnenie Bernulli dlya szhimaemoi zhidkosti.
Dinamika szhimaemoi zhidkosti baziruetsya takzhe na 2-m zakone N'yutona, zapisannom dlya edinicy massy zhidkosti. Ravnodeistvuyushaya sil davleniya i vneshnih sil sozdaet uskorenie edinicy massy, poetomu
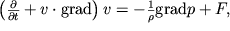
| (3.35) |
gde F - vneshnyaya sila, deistvuyushaya na edinicu massy. Dlya opredeleniya 5-ti neizvestnyh velichin (v
x, v
y, v
z, p i

) neobhodimo dopolnit' (3.35) material'nym uravneniem, svyazyvayushim plotnost' i davlenie:
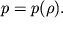
| (3.36) |
Sistema (3.34) - (3.36) nosit nazvanie uravnenii Eilera dlya szhimaemoi zhidkosti. Ogromnoe kolichestvo zadach gazodinamiki reshaetsya na osnove analiza etih uravnenii.
Vospol'zuemsya uravneniem (3.35) i poluchim uravnenie Bernulli. Dlya etogo vidoizmenim pravuyu chast' (3.35), vvedya vspomogatel'nuyu funkciyu
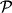
(2.27), i uchtem (2.29). Togda (3.35) primet vid
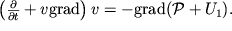
| (3.37) |
Pri stacionarnom techenii
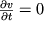
. V napravlenii osi trubki toka (vdol' krivolineinoi koordinaty

) mozhno zapisat'
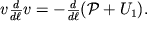
| (3.38) |
Poskol'ku potencial'naya energiya edinicy massy
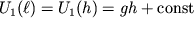
, a
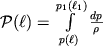
, to, po analogii s (3.13), perepishem (3.38) v vide:
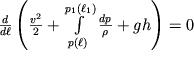
| (3.39) |
Integriruya (3.39) vdol' trubki toka, poluchaem uravnenie Bernulli dlya szhimaemoi zhidkosti
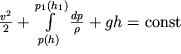
| (3.40) |
Zdes' h - polozhenie po vertikali secheniya trubki toka s koordinatoi

. Ochevidno, chto
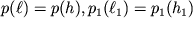
. Postoyannaya v (3.40) opredelyaetsya zadaniem skorosti v
1 i vysoty h
1 v fiksirovannom sechenii s koordinatoi
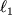
. S uchetom etogo, uravnenie (3.40) obretaet vid
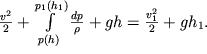
| (3.41) |
Dlya prakticheskogo ispol'zovaniya uravneniya Bernulli neobhodimo znanie material'noi svyazi mezhdu p i

. Dlya sluchaya neszhimaemoi zhidkosti (

= const) uravnenie (3.41) perehodit v (3.15).
Esli rech' idet o potoke gaza, to pri ego bystrom szhatii (uvelichenie plotnosti) gaz budet nagrevat'sya. Iz-za plohoi teploprovodnosti gaza teplo ne budet uspevat' uhodit' iz nagretyh oblastei. Poetomu dlya ustanovleniya material'noi svyazi
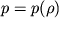
vospol'zuemsya adiabaticheskim priblizheniem:
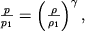
| (3.42) |
gde pokazatel' adiabaty
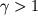
. Takaya svyaz' poluchaetsya iz pervogo nachala termodinamiki i uravneniya sostoyaniya ideal'nogo gaza (2.32) pri uslovii otsutstviya teploobmena mezhdu nagretoi oblast'yu i okruzhayushei sredoi. Davlenie v (3.42) vozrastaet s plotnost'yu bystree, chem pri izotermicheskom processe, tak kak
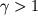
. V kurse molekulyarnoi fiziki budet pokazano. chto
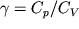
(C
p i C
V - teploemkosti pri postoyannyh davlenii i ob'eme sootvetstvenno). Dlya vozduha, sostoyashego glavnym obrazom iz dvuhatomnyh gazov,
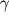
= 1,4.
Esli podstavit' (3.42) v (3.41) i vypolnit' prosteishee integrirovanie, to mozhno zapisat' vyrazhenie dlya raspredeleniya davleniya vdol' trubki toka:
![$p = p_1\left\{ 1 - \frac{\gamma - 1}{\gamma}\frac{\rho_1}{p_1}\left[\frac{1}{2}\left( v^2 - v_1^2\right) + g(h - h_1)\right]\right\}^{\frac{\gamma}{\gamma - 1}}.$](http://images.astronet.ru/pubd/2002/03/05/0001175083/tex/formula332.gif)
| (3.43) |
Ne umalyaya obshnosti, budem schitat' trubku toka gorizontal'noi (h=h
1). Polozhim dalee skorosti techeniya takimi, chto
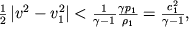
| (3.44) |
gde
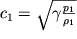
- parametr, imeyushii razmernost' skorosti. Kak my uvidim neskol'ko pozdnee, skorost' zvuka v gaze
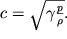
| (3.45) |
Pri normal'nyh usloviyah dlya atmosfery s=336 m/s. V etom sluchae (3.43) mozhno razlozhit' v ryad:
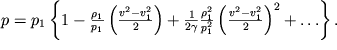
| (3.46) |
Esli prenebrech' kvadratichnym chlenom v (3.46), to raspredelenie davlenii sootvetstvuet techeniyu neszhimaemoi zhidkosti s plotnost'yu
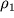
=const. Kvadratichnyi chlen nachinaet davat' vklad v raspredelenie davlenii pri skorostyah potoka, soizmerimyh so skorost'yu zvuka s
1.
Podstaviv (3.42) v (3.43), poluchaem raspredelenie plotnosti vdol' trubki toka:
![$\rho = \rho_1\left\{ 1 - \frac{\gamma - 1}{\gamma}\frac{\rho_1}{p_1}\left[\frac{1}{2}\left( v^2 - v_1^2\right) + g(h - h_1)\right]\right\}^{\frac{1}{\gamma - 2}}$](http://images.astronet.ru/pubd/2002/03/05/0001175083/tex/formula337.gif)
| (3.47) |
Dlya gorizontal'noi trubki toka i pri uslovii (3.44) raspredelenie plotnosti (3.47) imeet vid:
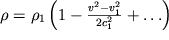
| (3.48) |
Takim obrazom, izmenenie plotnosti gaza neobhodimo prinimat' v uchet tol'ko pri skorostyah techeniya, sopostavimyh po poryadku velichiny so skorost'yu zvuka, opredelyaemoi, kak sleduet iz (3.45), davleniem i plotnost'yu v etom potoke.
Esli zhe skorost' techeniya
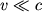
, to szhimaemost'yu gaza mozhno prenebrech' i operirovat' s nim, kak i s zhidkost'yu.
Nazad | Vpered

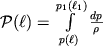 , to, po analogii s (3.13), perepishem (3.38) v vide:
, to, po analogii s (3.13), perepishem (3.38) v vide:
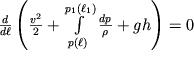
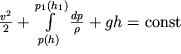
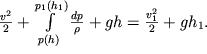
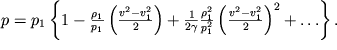
![$\rho = \rho_1\left\{ 1 - \frac{\gamma - 1}{\gamma}\frac{\rho_1}{p_1}\left[\frac{1}{2}\left( v^2 - v_1^2\right) + g(h - h_1)\right]\right\}^{\frac{1}{\gamma - 2}}$](http://images.astronet.ru/pubd/2002/03/05/0001175083/tex/formula337.gif)