Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Rasprostranenie vozmushenii davleniya i plotnosti.

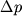
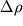
Esli v nepodvizhnoi zhidkosti ili gaze bystro sozdat' v nebol'shoi oblasti izbytochnoe davlenie $\Delta p$ , a znachit i izbytochnuyu plotnost' $\Delta\rho$ , to s techeniem vremeni eti vozmusheniya budut rasprostranyat'sya s nekotoroi skorost'yu, posledovatel'no privodya v dvizhenie chasticy sredy, raspolozhennye na puti rasprostraneniya. 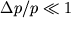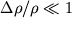Skorost' rasprostraneniya (kak pokazyvaet opyt) ne zavisit ot konkretnogo vida vozmusheniya, esli tol'ko otnositel'nye izmeneniya $\Delta p/p \ll 1$ i $\Delta\rho/\rho \ll 1$ (p i $\rho$ ravnovesnye znacheniya davleniya i plotnosti sredy). Vazhno otmetit', chto i forma takih malyh vozmushenii v processe ih rasprostraneniya ne menyaetsya. Rasschitaem skorost' rasprostraneniya vozmushenii, ispol'zuya samuyu prostuyu fizicheskuyu situaciyu. Pust' truba secheniem S zapolnena zhidkost'yu ili gazom s davleniem p i plotnost'yu $\rho$ . V moment vremeni t=0 porshen', zakryvayushii trubu s odnogo konca, nachinaet dvigat'sya s postoyannoi skorost'yu $v\ll c$ . 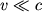Pered porshnem obrazuetsya oblast' povyshennogo davleniya (ris. 3.13), granica kotoroi budet dvigat'sya s neizvestnoi poka skorost'yu c. 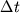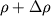Impul's sily F, prilozhennoi k porshnyu, za vremya $\Delta t$ privedet k dvizheniyu so skorost'yu v vse chasticy v ob'eme s povyshennoi plotnost'yu $\rho + \Delta\rho$ . Poetomu mozhem zapisat' ravenstvo:

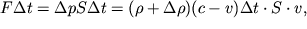
$F\Delta t = \Delta pS\Delta t = (\rho + \Delta\rho)(c - v)\Delta t\cdot S\cdot v,$

(3.49)

ili

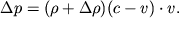
$\Delta p = (\rho + \Delta\rho)(c - v)\cdot v.$

(3.50)

Ris. 3.13.

Iz usloviya postoyanstva (do i posle szhatiya) massy vozduha sleduet, chto

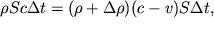
$\rho Sc\Delta t = (\rho + \Delta\rho)(c - v)S\Delta t,$

(3.51)

ili

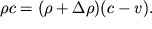
$\rho c = (\rho + \Delta\rho)(c - v).$

(3.52)

Reshaya sovmestno (3.50) i (3.52), nahodim skorost' dvizheniya chastic kak funkciyu izbytochnogo davleniya:

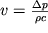
$v = \frac{\Delta p}{\rho c}$

(3.53)

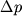
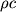
V akustike poslednee ravenstvo vyrazhaet akusticheskii zakon Oma. Esli provodit' analogiyu s zakonom Oma dlya uchastka cepi postoyannogo toka, izvestnogo iz shkoly, to v yavlyaetsya analogom sily toka, $\Delta p$ - raznosti potencialov, a $\rho c$ tak i nazyvaetsya - akusticheskoe soprotivlenie sredy. Ravenstvo (3.52) posle raskrytiya skobok imeet vid:

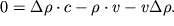
$0 = \Delta\rho\cdot c - \rho\cdot v - v\Delta\rho.$

(3.54)

Poslednii chlen v pravoi chasti (3.54) prenebrezhimo mal. Togda podstanovka (3.53) v (3.54) privodit k iskomomu vyrazheniyu dlya skorosti:

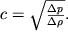
$c = \sqrt{\frac{\Delta p}{\Delta\rho}}.$

(3.55)

Formula (3.55) pozvolyaet rasschitat' skorost' zvuka razlichnyh zhidkostei i gazov, esli izvestna material'naya svyaz' mezhdu davleniem i plotnost'yu. Dlya vozduha eta svyaz' daetsya uravneniem adiabaty (3.42):

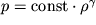
$p = {\rm const}\cdot\rho^\gamma$

(3.56)

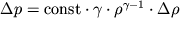
Poskol'ku $\Delta p = {\rm const}\cdot\gamma\cdot\rho^{\gamma - 1}\cdot\Delta\rho$ , to

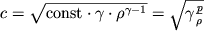
$c = \sqrt{{\rm const}\cdot\gamma\cdot\rho^{\gamma - 1}} = \sqrt{\gamma\frac{p}{\rho}}$

(3.57)

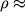
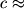
Pri normal'nyh usloviyah p = 10⁵ Pa, $\rho\approx$ 1,3 kg/m³ i $c\approx$ 336 m/c. Dlya vody, szhimaemost' kotoroi znachitel'no men'she, skorost' zvuka s = 1200 m/s. Otmetim, chto skorost' zvuka v vozduhe uvelichivaetsya s uvelicheniem ego ravnovesnoi plotnosti $\rho$ (3.57). Eto zamechanie nam ochen' prigoditsya dalee, kogda my budem rassmatrivat' rasprostranenie akusticheskih voln bol'shoi amplitudy.

Istechenie szhatogo gaza cherez soplo

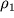
Rassmotrim odnu iz vazhneishih zadach gazodinamiki - istechenie gaza, predvaritel'no szhatogo v sosude do davleniya p₁ i plotnosti $\rho_1$ , cherez vyhodnuyu trubku peremennogo secheniya (soplo) (ris. 3.14). Skorost' istecheniya v, soglasno ravenstvu (3.43), poluchaetsya ravnoi

$v = \sqrt{v_1^2 + \frac{2\gamma}{\gamma - 1}\frac{p_1}{\rho_1}\left[1 - \left(\frac{p}{p_1}\right)^{\frac{\gamma - 1}{\gamma}}\right]}.$

(3.58)

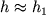
Zdes' uchteno, chto $h\approx h_1$ .

Ris. 3.14.

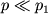
Pri malom sechenii sopla skorost' v₁ ochen' mala, i eyu mozhno prenebrech'. Nakonec, budem schitat', chto davlenie snaruzhi $p \ll p_1$ . Poetomu

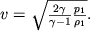
$v = \sqrt{\frac{2\gamma}{\gamma - 1}\frac{p_1}{\rho_1}}.$

(3.59)

Ocenka, provedennaya po etoi formule, dlya sluchaya, kogda vozduh pri normal'nyh usloviyah vytekaet v vakuum, daet velichinu skorosti v=750 m/n. Eta skorost' bolee chem vdvoe prevyshaet skorost' zvuka i, kak pokazyvaet opyt, pri ispol'zovanii suzhayushegosya sopla dostignuta byt' ne mozhet. Real'no vozduh dostigaet lish' skorosti zvuka, poskol'ku davlenie v sople nastol'ko vozrastaet, chto etot potok kak by zazhigaet soplo. Etot vyvod podtverzhdaetsya i prosteishimi raschetami. 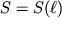Pust' $\ell$ - koordinata, napravlennaya vdol' osi sopla, peremennoe sechenie kotorogo $S = S(\ell)$ . Dlya stacionarnogo techeniya uravneniya Eilera (3.35) i uravnenie Bernulli (3.40) svyazyvayut prirashenie skorosti i davleniya:

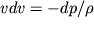
$vdv = - dp/\rho$

(3.60)

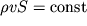
Iz usloviya postoyanstva massy (3.1) sleduet, chto v lyubom sechenii sopla $\rho vS = {\rm const}$ , ili

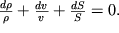
$\frac{d\rho}{\rho} + \frac{dv}{v} + \frac{dS}{S} = 0.$

(3.61)

Nakonec, soglasno (3.55), mozhem zapisat'

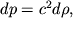
$dp = c^2 d\rho,$

(3.62)

gde c - skorost' zvuka v sechenii S, menyayushayasya vdol' sopla. Iz (3.60) i (3.62) imeem

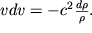
$vdv = - c^2 \frac{d\rho}{\rho}.$

(3.63)

Podstaviv (3.63) v (3.61), nahodim

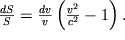
$\frac{dS}{S} = \frac{dv}{v}\left(\frac{v^2}{c^2} - 1\right).$

(3.31)

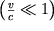
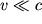
Takim obrazom, pri dozvukovyh skorostyah $\left(\frac{v}{c}\ll 1\right)$ pri suzhenii potoka (dS<0), skorost' vozrastaet (dv>0), a davlenie (soglasno 3.63) - ubyvaet. Odnako, po mere priblizheniya k skorosti zvuka c temp dostigaet nekotorogo maksimal'nogo znacheniya, ne prevyshayushego c. Pri rasshirenii potoka (dS>0) s nachal'noi skorost'yu $v \ll c$ , budet imet' mesto umen'shenie skorosti po potoku s odnovremennym rostom davleniya i plotnosti. Poluchit' sverhzvukovye skorosti mozhno lish' pri ispol'zovanii sopla, forma pokazana na ris. 3.15. V suzhayusheisya chasti sopla potok uskoryaetsya. 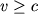Kogda ego skorost' v samom uzkom sechenii prevysit skorost' zvuka ( $v\ge c$ ), to, soglasno (3.64), uvelichenie secheniya (dS>0) budet privodit' k dal'neishemu uskoreniyu potoka. pri odnovremennom padenii davleniya i plotnosti. Takoe soplo, poluchivshee nazvanie sopla Lavalya (po imeni ego izobretatelya) pozvolyaet poluchit' sverhzvukovye skorosti potokov. Eta ideya chrezvychaino plodotvorno ispol'zuetsya pri konstruirovanii raketnyh dvigatelei. Na etom zhe principe postroena aerodinamicheskaya truba, v kotoruyu pomeshayutsya modeli sverhzukovyh samoletov.

Ris. 3.15.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce