Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Lekciya 4

Dvizhenie vyazkoi zhidkosti. Uravnenie Nav'e-Stoksa. Chislo Reinol'dsa. Formula Puazeilya. Laminarnoe i turbulentnoe techenie. Turbulentnost' atmosfery. Obtekanie tel potokom zhidkosti. Formula Zhukovskogo. Gidrodinamicheskoe podobie. Dvizhenie tela so sverhzvukovoi skorost'yu.

Sily vyazkogo treniya.

V predydushih lekciyah my rassmatrivali dvizhenie zhidkosti i gaza v prenebrezhenii silami vyazkogo treniya. Mezhdu tem, eti sily, deistvuyushie mezhdu chasticami dvizhusheisya zhidkosti, mogut kardinal'nym obrazom povliyat' kak na raspredelenie skorostei v potoke zhidkosti, tak i na obtekanie zhidkost'yu tel, pomeshennyh v dvizhushiisya potok. Eshe N'yuton ustanovil opytnym putem, chto pri skol'zhenii drug otnositel'no druga dvuh parallel'nyh ploskostei, prostranstvo mezhdu kotorymi zapolneno zhidkost'yu, sily vyazkogo treniya prepyatstvuyut etomu skol'zheniyu (ris. 4.1). Tak, pri dvizhenii so skorost'yu v verhnei ploskosti s ploshad'yu S otnositel'no nizhnei, voznikaet sila vyazkogo treniya, napravlennaya protiv dvizheniya i ravnaya

$F_\tau=\mu S\frac{v}{h}$

(4.1)

Eta sila proporcional'na ploshadi S i izmeneniyu skorosti na edinicu dliny v poperechnom napravlenii v/h (gradientu skorosti v napravlenii perpendikulyarnom dvizheniyu) i zavisit takzhe ot vyazkosti zhidkosti $\mu$ .

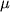
Ris. 4.1.

Formula (4.1) spravedliva, esli rasstoyanie h mezhdu plastinami znachitel'no men'she ih lineinyh razmerov $(h\ll\sqrt{S})$ . Vazhno otmetit', chto chasticy zhidkosti, prilegayushie k verhnei plastine, dvizhutsya vmeste s neyu so skorost'yu v (uvlekayutsya plastinoi). Naprotiv, chasticy zhidkosti vblizi nizhnei (nepodvizhnoi) plastiny nahodyatsya v pokoe (prilipayut k plastine). Esli myslenno razbit' zhidkost' na parallel'nye ploskie sloi, dvizhushiesya ravnomerno, to netrudno ponyat', chto kazhdyi vyshelezhashii sloi uvlekaet za soboi nizhnii sosednii sloi s siloi $F_\tau$ . 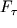V svoyu ochered', etot nizhnii sloi tormozit dvizhenie verhnego sloya s siloi, chislenno ravnoi $F_\tau$ . 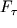Na kazhdyi sloi deistvuet sverhu i snizu dve ravnye, no protivopolozhnye sily. Skorost' sloev narastaet lineino s ih vysotoi (ris. 4.2), a sila treniya peredaetsya ot odnomu sloya k drugomu. Kak rezul'tat, usilie $F=F_\tau$ , prilozhennoi k verhnei plastine, peredaetsya na nizhnyuyu plastinu. Koefficient vyazkosti sredy opredelyaetsya eksperimental'no, naprimer, po skorosti ee istecheniya cherez trubku izvestnyh razmerov. (sm. nizhe). Kak pokazyvaet opyt s nagrevaniem, vyazkost' zhidkosti umen'shaetsya, a gazov - uvelichivaetsya. Ob'yasnenie takogo raznogo povedeniya koefficienta vyazkosti budet dano v kurse "Molekulyarnaya fizika".

Ris. 4.2.

Techenie vyazkoi zhidkosti. Uravnenie Nav'e-Stoksa.

Dlya analiza techeniya vyazkoi zhidkosti v pravuyu chast' uravneniya dvizheniya (3.28) neobhodimo dobavit' silu vyazkogo treniya, prilozhennuyu k edinice ob'ema zhidkosti. Dlya togo, chtoby izbezhat' lishnih vykladok, my ogranichimsya rassmotreniem dvumernogo sloistogo techeniya zhidkosti v napravlenii osi x, pri etom edinstvennaya komponenta skorosti v_x zavisit ot poperechnoi koordinaty y (ris. 4.3). Na verhnyuyu gran' dxdz kubika dxdydz (os' z perpendikulyarna ploskosti chertezha) v sootvetstvii s (4.1) v napravlenii osi x deistvuet uvlekayushaya sila $F'_{\tau_x}=\mu dxdz \left. \frac{dv_x}{dy}\right|_{y+dy}$ , a na nizhnyuyu gran' - tormozyashaya sila $F''_{\tau_x}=-\mu dxdz \left. \frac{dv_x}{dy}\right|_{y}$ . Poetomu ravnodeistvuyushaya sil vyazkogo treniya, prilozhennaya k vydelennomu kubiku, ravna

$F_\tau=F'_{\tau_x} + F''_{\tau_x}$

(4.2)

a sila, prilozhennaya k edinice ob'ema, sostavit

$f_{\tau_x}=\frac{F_\tau}{dxdydz}=\mu\frac{d^2 v_x}{dy^2}$

(4.3)

Pri lineinom zakone izmeneniya skorosti po vysote, kak na ris. 4.2, $f_\tau=0$ . Esli skorost' izmenyaetsya nelineino, kak na ris.4.3, to $f_\tau\ne 0$ . Pri trehmernom techenii zhidkosti sila vyazkogo treniya, voobshe govorya, imeet tri komponenty $f_{\tau}=\{f_{\tau_x}, f_{\tau_y}, f_{\tau_z}\}$ , gde

$\begin{array}{l} f_{\tau_x}=\mu \left( \frac{\partial ^2 v_x}{\partial x^2} +\frac{\partial ^2 v_x}{\partial y^2} + \frac{\partial ^2 v_x}{\partial z^2}\right) = \mu\Delta v_x \\ f_{\tau_y}=\mu \left( \frac{\partial ^2 v_y}{\partial x^2} +\frac{\partial ^2 v_y}{\partial y^2} + \frac{\partial ^2 v_y}{\partial z^2}\right) = \mu\Delta v_y \\ f_{\tau_z}=\mu \left( \frac{\partial ^2 v_z}{\partial x^2} +\frac{\partial ^2 v_z}{\partial y^2} + \frac{\partial ^2 v_z}{\partial z^2}\right) = \mu\Delta v_z \end{array}$

(4.4)

V (4.4) $\Delta=\frac{\partial ^2 }{\partial x^2}+\frac{\partial ^2 }{\partial y^2}+\frac{\partial ^2 }{\partial z^2}$ - operator Laplasa, shiroko primenyaemyi v fizike dlya sokrasheniya zapisi. Esli teper' komponenty sily treniya (4.4) podstavit' v pravye chasti uravnenii (3.29) dlya sootvetstvuyushih komponent skorostei, to my poluchim sistemu uravnenii gidrodinamiki vyazkoi zhidkosti. Eti tri uravneniya mogut byt' zapisany v vide odnogo vektornogo uravneniya

$\rho\left[ \frac{\partial}{\partial t} + {\bf v}\cdot {\rm grad}\right] {\bf v}= {\bf F} - {\rm grad }\; p + \mu\Delta {\bf v}$

(4.5)

Ono otlichaetsya ot (3.31) nalichiem v pravoi chasti chlena . Uravnenie (4.5) nazyvaetsya uravneniem Nav'e-Stoksa i yavlyaetsya osnovnym pri raschete dvizheniya vyazkoi neszhimaemoi zhidkosti. Odnako v obshem sluchae ono ne reshaetsya metodami sovremennoi matematiki, i na praktike prihoditsya ogranichivat'sya resheniem lish' chastnyh zadach. Odnoi iz takih zadach yavlyaetsya techenie nevyazkoi neszhimaemoi zhidkosti, podchinyayusheesya uravneniyu Bernulli. Ranee my poluchili uslovie, pri kotorom szhimaemost'yu zhidkosti ili gaza mozhno prenebrech'. Teper' my vyyasnim, v kakih sluchayah mozhno prenebrech' deistviem sil vyazkosti.

Ris. 4.3.

Chislo Reinol'dsa. Kriterii otsutstviya vyazkosti.

Rassmotrim techenie vyazkoi zhidkosti mezhdu dvumya gorizontal'nymi plastinami, rasstoyanie mezhdu kotorymi ravno h. Poskol'ku chasticy zhidkosti "prilipayut" k plastinam, to skorost' sloev tekushei zhidkosti budet razlichnoi. Kachestvenno raspredelenie skorostei sloev izobrazheno na ris. 4.4. Esli izvestna harakternaya skorost' techeniya (naprimer, skorost' v na osi potoka), to legko ocenit' sily vyazkogo treniya. Soglasno (4.3)

$f_{\tau_x}=\mu\frac{d^2 v_x}{dy^2}\sim \mu \frac{v}{h^2}.$

(4.6)

Otsyuda sleduet, chto sily vyazkogo treniya ubyvayut s uvelicheniem rasstoyaniya mezhdu plastinami. V obshem sluchae mozhno schitat', chto sily vyazkosti, voznikayushie v potoke, obratno proporcional'ny kvadratu harakternogo poperechnogo razmera potoka i proporcional'ny skorosti.

Ris. 4.4.

S tochki zreniya dinamiki (sm. uravnenie 4.5) pri otsutstvii vneshnih sil F vyazkost'yu mozhno prenebrech', esli sily davleniya -grad p znachitel'no prevoshodyat sily vyazkosti $\mu\Delta{\bf v}$ . Na pervyi vzglyad, pri techenii zhidkosti mezhdu parallel'nymi plastinami (ravno kak i po trube postoyannogo secheniya), gde gradienty davlenii otsutstvuyut vovse, vyazkost'yu v principe nel'zya prenebrech'. I vse nashi vyvody o techenii ideal'noi zhidkosti stanovyatsya nevernymi. Odnako nado prinyat' vo vnimanie, chto iz-za fluktuacii linii toka "norovyat" iskrivit'sya, i chasticy v nih dvizhutsya s uskoreniem. Poetomu davleniya p₁ i p₂ po raznye storony izognutoi trubki toka budut razlichnymi: p₂>p₁ (ris. 4.5). Voznikayushie gradienty davleniya obespechivayut krivolineinoe techenie zhidkosti:

$\rho\frac{d\vec v}{dt}\cong - {\rm grad} \; p$

(4.7)

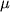
Poslednee uravnenie yavlyaetsya priblizhennym uravneniem Nav'e-Stoksa ( $\mu$ =0) i zapisano v otsutstvii vneshnih sil. Togda kriterii malosti sil vyazkosti svoditsya k neravenstvu

$\frac{|\mu\Delta v|}{|{\rm grad}\; p|}\approx \frac{|\mu\Delta v|}{|\rho\frac{dv}{dt}|}<1$

(4.8)

V gidrodinamike ochen' chasto ispol'zuyut ponyatie sily inercii F_i=- $\rho$ dv/dt. S tochki zreniya nablyudatelya, dvizhushegosya vmeste s chasticei zhidkosti, ona nahoditsya v pokoe, potomu chto sily davleniya, vyazkosti i inercii uravnoveshivayut drug druga (sm. 4.5):

${\bf F}_i - {\rm grad}\; p +\mu\Delta {\bf v} = 0$

(4.9)

Neravenstvo (4.8) oznachaet, chto sily vyazkosti znachitel'no men'she sil inercii. V chastnom sluchae techeniya zhidkosti mezhdu plastinami sily inercii pri iskrivlenii trubok toka zhidkosti

$F_i = -\rho \frac{dv}{dt}\sim -\rho \frac{v^2}{h},$

(4.10)

gde v²/h - harakternoe centrostremitel'noe uskorenie. V obshem sluchae, sily inercii obratno proporcional'ny poperechnomu razmeru potoka i proporcional'ny kvadratu skorosti. S uchetom ocenok (4.6) i (4.10) uslovie (4.8) perepishetsya sleduyushim obrazom:

$\frac{\mu\frac{v}{h^2}}{\rho\frac{v^2}{h}}=\frac{\mu}{\rho v h}=\frac{1}{{\rm Re}}<1$

(4.11)

Zdes' ${\rm Re}=\frac{\rho vh}{\mu}$ - chislo Reinol'dsa, harakterizuyushee otnoshenie sil inercii i sil vyazkosti. Takim obrazom, tekushuyu zhidkost' mozhno rassmatrivat' kak nevyazkuyu, esli chislo Reinol'dsa dlya takogo techeniya Re>1. Odnako i v etom sluchae vyazkost' igraet vspomogatel'nuyu rol'. Pri ne ochen' vysokih skorostyah techeniya sily vyazkosti "gasyat" komponenty skorosti zhidkosti, poperechnye k potoku, prepyatstvuya, tem samym, vozniknoveniyu neustoichivogo techeniya (sm. nizhe).

Ris. 4.5.

Dadim nekotorye ocenki techeniya zhidkosti po krugloi trube radiusa R. Chislo Reinol'dsa v etom sluchae ${\rm Re}=\frac{\rho vR}{\mu}$ . Esli prinyat' radius truby R = 1 sm i skorost' techeniya v = 1 sm/s, to dlya vody ( $\rho$ =10³ kg/m³, pri t=15 $^\circ C$ ) chislo Re=86. Eto oznachaet, chto sily vyazkosti ne sushestvenny, i vodu mozhno rassmatrivat' kak nevyazkuyu zhidkost'. Odnako eto priblizhenie stanovitsya nespravedlivym, esli radius trubki umen'shit' na dva poryadka, i Re=0,86<1. Pri takom techenii raspredelenie davlenii i skorostei v potoke uzhe ne podchinyaetsya uravneniyu Bernulli. 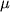Eshe v bol'shei stepeni eto otnositsya k vyazkomu glicerinu ( $\mu$ =1,4 kg/(m*s)). 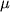Pri techenii vozduha po trube ( $\rho$ =1,3 kg/m³, $\mu$ =1,8*10^-5 kg/(m*s)) chislo Reinol'dsa priblizitel'no na poryadok men'she, chem pri analogichnom techenii vody. Eto ukazyvaet na to, chto sily vyazkosti pri techenii vozduha i drugih gazov igrayut bol'shuyu rol', chem pri analogichnom techenii vody.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce