Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Techenie vyazkoi zhidkosti. Formula Puazeilya.

Rassmotrim techenie vyazkoi zhidkosti, obrativshis' neposredstvenno k opytu. Podklyuchim tonkuyu gorizontal'nuyu steklyannuyu trubu s vpayannymi v nee vertikal'nymi manometricheskimi trubkami pri pomoshi rezinovogo shlanga k vodoprovodnomu kranu (ris. 4.6).

Ris. 4.6.

Pri nebol'shoi skorosti techeniya vody legko usmatrivaetsya ponizhenie urovnya vody v manometricheskih trubkah v napravlenii techeniya (h1>h2>h3). Eto v svoyu ochered' ukazyvaet na nalichie gorizontal'nogo gradienta davleniya - staticheskoe davlenie zhidkosti umen'shaetsya vdol' potoka. Pri ravnomernom pryamolineinom techenii zhidkosti sily davleniya uravnoveshivayutsya silami vyazkosti, a sily inercii otsutstvuyut vovse. Uravnenie Nav'e-Stoksa dlya etogo sluchaya zapishetsya v vide

$- {\rm grad }\; p + \mu\Delta {\bf v} = 0.$

(4.12)

Raspredelenie skorostei v poperechnom sechenii potoka vyazkoi zhidkosti mozhno nablyudat' pri ee vytekanii iz vertikal'noi trubki cherez uzkoe otverstie (ris. 4.7).

Ris. 4.7.

Esli, naprimer, pri zakrytom krane K nalit' vnachale podkrashennyi saharnyi sirop, a zatem poverh ostorozhno nalit' nepodkrashennyi sirop, to v sostoyanii ravnovesiya granica razdela G budet gorizontal'noi. Esli kran K otkryt', to granica razdela primet formu, pohozhuyu na paraboloid vrasheniya. Eto ukazyvaet na sushestvovanie raspredeleniya skorostei v sechenii trubki pri vyazkom techenii siropa. Netrudno vychislit' eto raspredelenie skorostei potoka v poperechnom ego sechenii. Eto mozhno sdelat', zapisav uravnenie (4.12) v cilindricheskih koordinatah (x, r) i prointegrirovav ego. Odnako my postupim neskol'ko proshe, esli priravnyaem sily vyazkosti i davleniya, deistvuyushie na cilindricheskii ob'em zhidkosti radiusa r i dlinoi dx (ris. 4.8):

$(p(x) - p(x+dx))\pi r^2 + \mu 2\pi rdx\frac{dv}{dr}=0.$

(4.13)

Otmetim, chto ravnodeistvuyushaya sil davleniya napravlena po potoku (vdol' osi x), a sila vyazkogo treniya, prilozhennaya k bokovoi poverhnosti cilindricheskogo ob'ema - protiv potoka, poskol'ku dv/dr<0. Proizvedya sokrashenie i razdeliv (4.13) na dx, poluchaem

$-\frac{dp}{dx} + \mu\frac{2}{r}\frac{dv}{dr}=0.$

(4.14)

Velichina gradienta davleniya dp/dx v (4.14) ne zavisit ot radiusa r, t.k. davlenie p=p(x) i v poperechnom sechenii x=const ne menyaetsya. Eto pozvolyaet prointegrirovat' (4.14) po radiusu:

$\frac{dp}{dx}\int\limits_R^r rdr = 2\mu\int\limits_0^v dv.$

(4.15)

Uravnenie (4.15) pozvolyaet rasschitat' raspredelenie skorostei , pri uslovii, chto u stenok truby eta skorost' ravna nulyu. Posle integrirovaniya (4.15) poluchaem

$v(r) = -\frac{1}{4\mu}\frac{dp}{dx}(R^2 - r^2).$

(4.16)

Davlenie ravnomerno padaet v napravlenii osi x, poetomu dp/dx<0 i ne zavisit ot x. Parabolicheskoe raspredelenie skorostei (4.16) graficheski izobrazheno na ris. 4.8 u vyhodnogo secheniya truby. Potok vektora skorosti cherez poperechnoe sechenie truby, ili zhidkosti, protekayushei cherez sechenie v edinicu vremeni (na praktike upotreblyayut termin "rashod zhidkosti") okazyvaetsya ravnym

$N_v = \int vdS = \int\limits_0^R v(r)2\pi rdr = \frac{\pi R^4}{8\mu}\left(-\frac{dp}{dx}\right).$

(4.17)

Dlya prakticheskih celei rashod zhidkosti opredelyayut po formule Puazeilya

$N_v = \frac{\pi R^4}{8\mu}\frac{p_1 - p_2}{\ell}.$

(4.18)

Zdes' rashod vody N_v proporcionalen raznosti davlenii p₁-p₂ na koncah truby dlinoi $\ell$ . Sleduet obratit' vnimanie na sushestvennuyu zavisimost' propusknoi sposobnosti truby ot ee radiusa R. Pri zadannom davlenii na vhode vodoprovodnoi seti uvelichenie diametra trub vdvoe vlechet uvelichenie ih propusknoi sposobnosti v 16 raz!

Ris. 4.8.

Pol'zuyas' formuloi Puazeilya mozhno opredelit' vyazkost' zhidkosti. Tak, naprimer, v opyte, izobrazhennom na ris. 4.6, legko izmerit' raznost' davlenii i rashod zhidkosti i pri izvestnom radiuse gorizontal'noi trubki poschitat' vyazkost' zhidkosti Odnako bolee udobno vyazkost' zhidkosti opredelyat' po metodu Stoksa, izmeryaya vremya padeniya sharika v etoi zhidkosti (sm. nizhe). Parabolicheskii profil' skorosti sloev, kak netrudno podschitat', budet i pri techenii zhidkosti mezhdu dvumya plastinami (ris. 4.4). 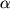Esli etot risunok razrezat' poseredine na vysote i naklonit' nizhnyuyu plastinu pod uglom $\alpha$ , to my poluchim kartinu sloistogo techeniya vody v reke pod deistviem sily tyazhesti (ris. 4.9). Vmesto perepada davleniya dp/dx my mozhem ispol'zovat' komponentu sily tyazhesti $F_x = \rho g\sin\alpha$ pri raschete profilya skorostei techeniya.

Ris. 4.9.

Laminarnoe i turbulentnoe techenie.

Obratimsya teper' k voprosu ob ustoichivosti techeniya zhidkosti po trubam. S etoi cel'yu postavim sleduyushii eksperiment. Pust' zhidkost' vytekaet iz sosuda cherez gorizontal'nuyu steklyannuyu trubku (ris. 4.10). Dlya kontrolya za harakterom techeniya budem pri pomoshi kapillyara vpuskat' tu zhe, no okrashennuyu zhidkost' vo vhodnoe sechenie trubki.

Ris. 4.10.

V sluchae malogo poperechnogo secheniya truby i ne ochen' bol'shoi skorosti techeniya okrashennaya struika dvizhetsya pryamolineino strogo vdol' osi truby (situaciya a na ris. 4.10). Pri bol'shem sechenii ili pri udvoenii skorosti poyavlyaetsya neregulyarnoe dvizhenie, kogda struika razbivaetsya na mnozhestvo izvilistyh struek (situaciya b). V pervom sluchae dvizhenie nazyvaetsya sloistym, ili laminarnym, a vo vtorom sluchae - turbulentnym. Pri laminarnom techenii sily vyazkosti sglazhivayut bokovye dvizheniya zhidkosti, voznikayushie vsledstvie razlichnyh nerovnostei stenok truby. Inerciya zhidkosti stremitsya sohranit' bokovye dvizheniya zhidkosti, sposobstvuya tem samym turbulentnosti. Perehod ot laminarnogo k turbulentnomu techeniyu privodit pri nekotorom chisle Reinol'dsa, poluchivshego nazvanie kriticheskogo:

${\rm Re_{kr}} = \left(\frac{\rho vR}{\mu}\right)_{kr}.$

(4.19)

Ego znachenie sil'no zavisit ot formy vhodnoi chasti truby. V sluchae zakruglennogo konca, kak na ris. 4.10, techenie s samogo nachala ustanavlivaetsya laminarnym i prodolzhaet ostavat'sya takim do bol'shih chisel Reinol'dsa. Oblast' kriticheskih chisel Re_kr lezhit mezhdu znacheniyami 1200 (nezakruglennyi vhod) i 20000 (zakruglennyi vhod). Poetomu v literature privodyatsya ves'ma razlichnye znacheniya Re_kr.

Ris. 4.11.

Pri stacionarnom turbulentnom techenii skorost' v dannoi tochke sluchainym obrazom menyaetsya vo vremeni, odnako srednee znachenie vektora skorosti <v> napravleno vdol' osi truby. Srednyaya skorost' ostaetsya postoyannoi po secheniyu truby, i tol'ko v ochen' tonkom pogranichnom sloe spadaet do nulya u stenok truby. Na praktike dlya rascheta turbulentnogo techeniya zhidkosti po trube ispol'zuetsya formula

$p_1 - p_2 = k\rho \left \lt v\right\gt^2\frac{\ell}{R},$

(4.20)

v kotoroi k - bezrazmernyi gidravlicheskii koefficient. Srednyaya zhe po secheniyu skorost' laminarnogo techeniya iz formuly Puazeilya (4.18) poluchaetsya ravnoi

$\left\lt v\right\gt = \frac{N_v}{\pi R^2} = \frac{R^2}{8\mu}\frac{p_1 - p_2}{\ell}.$

(4.21)

Raznost' davlenii, kak funkciya skorosti

$p_1 - p_2 = \frac{8\mu}{R}\left\lt v\right\gt\frac{\ell}{R}.$

(4.22)

Esli sravnit' perepady davlenii dlya turbulentnogo (4.20) i laminarnogo (4.22) techenii, to legko videt', chto povyshenie skorosti prokachki zhidkosti po trubam pri turbulentnom techenii potrebuet znachitel'no bol'shego uvelicheniya perepada davlenii, chem pri laminarnom. Izvesten istoricheskii fakt prokladki nefteprovoda v Rossii, sproektirovannogo na osnove formuly (4.20). Odnako pri prilozhennoi raznosti davlenii propusknaya sposobnost' nefteprovoda okazalas' vyshe raschetnoi. Oshibka proekta (k schast'yu, udachnaya) sostoyala v tom, chto nesmotrya na bol'shoi diametr trub nefteprovoda vyazkaya neft' techet laminarno, i propusknaya sposobnost' nefteprovoda dolzhna rasschityvat'sya po formule (4.22). Formuly (4.20) i (4.22) mozhno ob'edinit' v odnu, esli prinyat', chto bezrazmernyi gidravlicheskii koefficient v (4.20) zavisit ot chisla Reinol'dsa: k = k₀ + 8/Re. Togda pri Re>Re_kr k $\approx$ k₀, i techenie turbulentnoe. Naprotiv, pri Re $\le$ 1 k $\approx$ 8/Re, i formula (4.20) perehodit v (4.22). Na ris. (4.12) izobrazhen grafik zavisimosti perepada davleniya v trubah v zavisimosti ot skorosti techeniya. Odnako esli dvigat' trubu otnositel'no nepodvizhnoi zhidkosti, to krivuyu na ris. 4.12 s izvestnoi natyazhkoi mozhno interpretirovat' kak zavisimost' sily lobovogo soprotivleniya, prihodyasheisya na edinicu ploshadi secheniya truby, ot skorosti ee dvizheniya v zhidkosti. Pri malyh skorostyah dvizheniya sila soprotivleniya proporcional'na skorosti, a pri bol'shih - kvadratu skorosti.

Ris. 4.12.

Pri svobodnom laminarnom techenii (v otsutstvie napravlyayushih poverhnostei) strui zhidkosti razvivayutsya neustoichivosti, i laminarnoe techenie perehodit v turbulentnoe. Na ris. 4.13. predstavleno opticheskoe izobrazhenie tekushei strui zhidkosti (chislo Reinol'dsa Re=250). Horosho vidno, chto techenie ot laminarnogo rezhima cherez perehodnyi transformiruetsya v turbulentnyi. Do nastoyashego vremeni net yasnogo ponimaniya, pochemu eto proishodit. Klassicheskaya lineinaya teoriya ustoichivosti daet vernoe opisanie nachal'noi stadii razrusheniya laminarnogo techeniya. Yasno, chto perehod k turbulentnomu techeniyu yavlyaetsya sushestvenno nelineinym processom, i teoriya ustoichivosti dolzhna bazirovat'sya na analize nelineinyh davlenii gidrodinamiki.

Ris. 4.13.

My otmetim, chto v oblasti laminarnogo techeniya linii toka prakticheski parallel'ny. Pole skorostei yavlyaetsya potencial'nym (po analogii s odnorodnym polem sily tyazhesti). Opisanie techeniya mozhet byt' znachitel'no proshe, esli ispol'zovat' potencial skorostei

$\Phi (r) = \int\limits_{r_0}^r v(r)dr.$

(4.23)

V ryade zadach proshe rasschitat' snachala potencial skorostei, a zatem i skorost': v = -grad F V oblasti turbulentnogo techeniya nevozmozhno vvesti odnoznachno potencial skorostei. Skorost' techeniya v v kazhdoi tochke yavlyaetsya sluchainoi funkciei vremeni, i neobhodimo razvivat' statisticheskii podhod k opisaniyu turbulentnogo techeniya. Ochen' plodotvornym yavlyaetsya ponyatie vihrya. S matematicheskoi tochki zreniya vihrevoi harakter techeniya imeet mesto togda, kogda otlichna ot nulya "rabota" vektora skorosti v po zamknutomu konturu, poluchivshaya nazvanie cirkulyacii vektora skorosti:

$\Gamma = \oint\limits_{\ell} vd\ell \ne 0.$

(4.24)

Na ris. 4.14 shematichno izobrazheny linii toka v fiksirovannyi moment vremeni pri turbulentnom techenii i pokazan kontur $\ell$ , po kotoromu vychislyaetsya integral (4.24). Simvol $\oint$ oznachaet, chto integrirovanie proizvoditsya po zamknutomu konturu. Esli razmery kontura styagivat' v tochku, to v etoi tochke intensivnost' vihreobraznogo techeniya budet harakterizovat'sya rotorom vektora skorosti v sootvetstvii s opredeleniem

$({\rm rot}\; {\bf v})_n = \lim_{\Delta S\to 0}\frac{\Gamma}{\Delta S}.$

(4.25)

Zdes' $\Delta S$ - ploshad' malen'kogo kontura, n - normal' k etoi ploshadke, napravlennaya tuda zhe, kuda i ostrie buravchika, rukoyatka kotorogo vrashaetsya v napravlenii techeniya. Formula (4.25) daet lish' znachenie proekcii vektora rot v na napravlenii normali, poskol'ku kontur orientirovan proizvol'no. Chtoby poschitat' komponenty vektora rot v nado vychislit' cirkulyacii po konturam, normali k kotorym sovpadayut s sootvetstvuyushimi osyami koordinat.

Ris. 4.14.

V kachestve illyustracii k skazannomu poschitaem rotor vihrevogo techeniya vody, podobno tomu, kotoroe imeet mesto vblizi vypusknogo otverstiya vanny. Esli prinyat', chto chasticy dvizhutsya s uglovoi skorost'yu $\omega$ , to cirkulyaciya vektora skorosti po kruglomu konturu radiusa r s centrom na osi slivnogo otverstiya i perpendikulyarnogo k nei ravna

$\Gamma = v\cdot 2\pi r = \omega r2\pi r = 2\pi r^2\omega.$

(4.26)

Pri takoi orientacii kontura vektor rot v budet napravlen po normali n k konturu i raven

${\rm rot}\; {\bf v}=\frac{\Gamma}{\Delta S}{\bf n } = \frac{2\pi r^2 \omega}{\pi r^2}{\bf n}= 2 {\bf \omega}.$

(4.27)

Provedem bez dokazatel'stva formulu dlya vektora rot v v dekartovyh koordinatah:

${\rm rot}\; {\bf v}= \left( \frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z}\right){\bf i} + \left( \frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x}\right){\bf j}+ \left( \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}\right){\bf k}.$

(4.28)

Zdes' i, j i k - edinichnye vektory vdol' sootvetstvuyushih dekartovyh osei koordinat. Zhelayushie mogut podschitat' (4.27), pol'zuyas' formuloi (4.28).

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce