Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

O turbulentnosti atmosfery.

Pri opisanii atmosfery my otmechali, chto v nizhnem (prizemnom) sloe proishodit intensivnoe konvektivnoe peremeshivanie vozduha. Skorost' vozdushnyh potokov v kazhdoi tochke yavlyaetsya sluchainoi funkciei vremeni. Eto podtverzhdaetsya, naprimer, opticheskim yavleniem mercaniya zvezd, svet ot kotoryh rasseivaetsya na sluchainyh oblastyah s povyshennoi i ponizhennoi plotnost'yu atmosfery. Eto yavlenie analogichno drozhaniyu i iskazheniyu ob'ektov, nablyudaemyh cherez prostranstvo s s sil'nym ispareniem vody posle dozhdya v tepluyu pogodu ili benzina na avtozapravochnyh stanciyah. Variacii skorosti v potokah atmosfery takzhe yavlyayutsya turbulentnymi, poetomu opisanie dvizheniya atmosfery trebuet statisticheskogo podhoda. Osushestvit' v polnom ob'eme takoe opisanie nevozmozhno. Ochen' plodotvornym yavlyaetsya predstavlenie turbulentnyh potokov v vide sovokupnosti vihrei ot velichiny $\ell_0\sim 1$ mm do velichiny L₀~1 m. Eti velichiny nosyat nazvanie vnutrennego i vneshnego masshtabov turbulentnosti, prichem oba masshtaba vozrastayut pri udalenii ot poverhnosti Zemli. Vnutrennii masshtab voznikaet kak rezul'tat posledovatel'nogo raspada bol'shih, no neustoichivyh vihrei na bolee melkie, kotorye, v svoyu ochered' raspadayutsya dol'she vplot' do vihrei razmerom poryadka neskol'kih millimetrov. Ocenku velichiny vnutrennego masshtaba mozhno poluchit' iz sleduyushih prostyh soobrazhenii. Esli v potoke, dvizhushemsya so skorost'yu v imeetsya neodnorodnost' s lineinym razmerom $\sim\ell$ , to kineticheskaya energiya perenosimaya neodnorodnost'yu

$E_k=\frac{mv^2}{2}\sim \rho\ell^3 v^2.$

(4.29)

Iz-za nalichiya vyazkosti chast' etoi energii dissipiruet v teplo. Esli neodnorodnost' smeshaetsya na rasstoyanie $\sim\ell$ , to kolichestvo tepla Q ravno rabote sil vyazkogo treniya

$Q=F_{tr}\cdot \ell \sim \mu \frac{ v}{\ell}S\ell\sim \mu v \ell^2.$

(4.30)

Zdes' uchteno, chto $\frac{dv}{d\ell}\sim \frac{v}{\ell};\; S\sim \ell^2$ - ploshad' poverhnosti neodnorodnosti, k kotoroi prilozhena sila vyazkosti. Otnoshenie kineticheskoi energii k kolichestvu teploty priblizitel'no ravno chislu Reinol'dsa:

$\frac{E_k}{Q}\cong \frac{\rho v\ell}{\mu}= {\rm Re}.$

(4.31)

Esli E_k>Q (Re>1), to sily inercii prevoshodyat sily vyazkosti. V takom intervale skorostei, nazyvaemym inercionnym intervalom, vihri raspadayutsya na bolee melkie, u kotoryh chislo Reinol'dsa Re~1. Pri skorostyah techeniya v~1 sm/s takomu chislu Reinol'dsa sootvetstvuet $\ell$ ~1 mm, chto po poryadku velichiny sovpadaet so vnutrennim masshtabom turbulentnosti.

Ris. 4.15.

Ishodya iz takogo predstavleniya, A.N. Kolmogorov rassmotrel izmenenie vo vremeni raznosti skorostei v dvuh tochkah prostranstva, raznesennyh na rasstoyanie $\ell$ (ris. 4.15). On ustanovil, chto srednii kvadrat raznosti skorostei $\left\lt [ v(r+\ell) -v(r)]^2 \right\gt$ mozhno opisat' universal'noi zavisimost'yu v inercionnom intervale $\ell_0 < |\ell|< L_0$ . Dlya komponent vektora skorosti, napravlennyh vdol' $\ell$

$D_{\ell\ell}= \left\lt [ v_{\ell}(r+\ell) -v_{\ell}(r)]^2 \right\gt= C_v^2 \ell^{2/3}.$

(4.32)

Funkciya $D_{\ell\ell}$ nazyvaetsya strukturnoi funkciei pul'sacii skorosti i opisyvaetsya universal'noi zavisimost'yu $\ell^{2/3}$ . Ona ne zavisit ot r vsledstvie statisticheskoi odnorodnosti pul'sacii skorosti, i ne zavisit ot napravleniya raznosa tochek, a tol'ko ot velichiny $\ell$ . Poslednee yavlyaetsya rezul'tatom statisticheskoi izotropnosti turbulentnosti. Strukturnaya funkciya dlya poperechnyh komponent v_t $D_{tt}= \left\lt [ v_{t}(r+\ell) -v_{t}(r)]^2 \right\gt$ s uchetom neszhimaemosti atmosfery (div v=0) vyrazhaetsya cherez $D_{\ell\ell}$ sleduyushim obrazom:

$D_{tt}=\frac{1}{2\ell}\frac{d}{d\ell}\left( \ell^2 D_{\ell\ell} \right).$

(4.33)

C_v² nazyvaetsya strukturnaya postoyannaya skorosti i harakterizuet obshee kolichestvo energii turbulentnosti. Strukturnaya funkciya skorostei $D_{\ell\ell}$ pozvolyaet rasschitat' strukturnuyu funkciyu fluktuacii temperatury, podchinyayusheisya takzhe zakonu "2/3":

$D_{TT}=\left\lt [ T(r+\ell) -T(r)]^2 \right\gt=C^2_T\ell^{2/3}.$

(4.34)

Vyvod etoi formuly mozhet byt' vypolnen na osnove usredneniya reshenii uravnenii gidrodinamiki i teploperenosa pri uchete (4.32), chto vyhodit za ramki nashego kursa. Strukturnaya postoyannaya temperatury C_T² mozhet byt' rasschitana, esli izmerit' mikropul'sacii temperatury s pomosh'yu chuvstvitel'nyh, raznesennyh na rasstoyanie $\ell$ , datchikov i usrednit' rezul'taty za dlitel'nyi (poryadka 1 chasa) otrezok vremeni. Takie datchiki ustanavlivayutsya na machtah, sharah-zondah i samoletah. V nastoyashee vremya shirokoe primenenie poluchili metody akusticheskoi lokacii, pozvolyayushie izuchat' vysotnuyu zavisimost' C_T² vplot' do vysot ~1 km. Eti metody osnovany na tom, chto uchastki atmosfery s intensivnymi fluktuaciyami temperatury (i, sledovatel'no, plotnosti) sil'nee otrazhayut akusticheskie impul'sy, chem uchastki so slabymi temperaturnymi fluktuaciyami. Vysotnaya zavisimost' C_T², poluchennaya akusticheskim metodom, izobrazhena na ris. 4.16. Hotya fluktuacii temperatury sostavlyayut sotye (i dazhe men'she) doli gradusa, tem ne menee oni privodyat k fluktuaciyam pokazatelya prelomleniya n. Strukturnaya funkciya n poluchaetsya iz material'nogo uravneniya n=n(p, T) (p i T - ravnovesnye znacheniya davleniya i temperatury) i takzhe podchinyaetsya universal'nomu zakonu "2/3":

$D_{nn}=\left\lt [ n(r+\ell) -n(r)]^2 \right\gt=C^2_n\ell^{2/3}.$

(4.35)

Velichina C_n² nazyvaetsya strukturnoi postoyannoi pokazatelya prelomleniya i lezhit v predelah 10^-15m^-2/3<C_n²<10^-14 m^-2/3. Ona legko podschityvaetsya iz uravneniya n=n(p, T), esli izvestna C_T².

Ris. 4.16.

Formula (4.35) igraet fundamental'nuyu rol' v zadachah rasprostraneniya svetovyh voln cherez atmosferu, vydelennyh v samostoyatel'nuyu nauku - atmosfernuyu optiku. Na ris. 4.17 (a) privedeny rezul'taty komp'yuternogo modelirovaniya mgnovennogo izobrazheniya zdaniya Moskovskogo universiteta, rassmatrivaemogo cherez turbulentnuyu atmosferu v podzornuyu trubu s rasstoyaniya v neskol'ko kilometrov. S techeniem vremeni eto izobrazhenie, razumeetsya, budet haoticheski menyat'sya. Odnako pri izvestnom raspredelenii fluktuacii pokazatelya prelomleniya s pomosh'yu komp'yuternyh metodov obrabotki izobrazhenii mozhno ustranit' turbulentnye iskazheniya (ris. 4.17 b).

Ris. 4.17.

Vzaimodeistvie tela s potokom ideal'noi zhidkosti.

Odnoi iz vazhneishih problem gidro i aerodinamiki yavlyaetsya vsestoronnee issledovanie i ustanovlenie osnovnyh zakonomernostei vozdeistviya potokov zhidkosti i gaza na obtekaemye imi tela. Eta oblast' znanii priobrela isklyuchitel'noe znachenie pri proektirovanii gidroelektrostancii, vetryanyh dvigatelei, v turbinostroenii, razvitii aviacii i dr. Eshe I. N'yutonom byla sformulirovana udarnaya teoriya, baziruyushayasya na predstavlenii vozduha v vide otdel'nyh ne svyazannyh drug s drugom material'nyh chastic. 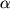Soglasno ego teorii sila davleniya vozdushnogo potoka na ploshadku S, podstavlennuyu pod uglom $\alpha$ (uglom ataki) k napravleniyu potoka ravna

$F=\rho S v^2 \sin^2 \alpha.$

(4.36)

Eta formula legko poluchaetsya, esli poschitat' impul's, peredavaemyi ploshadke v edinicu vremeni neuprugo vzaimodeistvuyushei s nei struei (ris. 4.18). Opytnaya proverka etoi formuly pokazala, chto ona neverno opisyvaet zavisimost' sily F ot ugla ataki. (I tol'ko pri skorostyah potoka, znachitel'no bol'shih skorosti zvuka v etoi zhidkosti, formula N'yutona okazyvaetsya spravedlivoi, chto podtverzhdaetsya opytnym putem). Na samom dele velichina etoi sily proporcional'na $\sin\alpha$ . Esli by formula (4.36) byla by verna, to eto oznachalo by nevozmozhnost' poletov na apparatah tyazhelee vozduha. Vse eto govorit o tom, chto model' zhidkosti kak sovokupnosti diskretnyh chastic yavlyaetsya nevernoi. Real'nye zhe sily mogut byt' poschitany na osnove gidrodinamicheskogo podhoda, uchityvayushego obtekanie tela dvizhushimsya potokom kontinual'noi sredy.

Ris. 4.18.

Proillyustriruem skazannoe na prosteishem primere. Pust' v dvizhushemsya so skorost'yu v₀ potoke pomesheny disk i shar odinakovogo radiusa r (ris. 4.19).

Ris. 4.19.

V centre diska v tochke K, nazyvaemoi kriticheskoi, potok ostanavlivaetsya (v=0), i davlenie, soglasno uravneniyu Bernulli

$p_k=p_0+\frac{\rho v_0^2 }{2}.$

(4.37)

Eto davlenie bol'she staticheskogo davleniya v potoke p₀ na velichinu $\frac{\rho v_0^2}{2}$ , poluchivshuyu ranee nazvanie dinamicheskogo davleniya, ili dinamicheskogo napora. Iz-za povorota trubok toka na 90 $^\circ$ davlenie v drugih tochkah na poverhnosti diska budet takim zhe, kak i v tochke K. Poetomu, esli pozadi diska davlenie ravno p₀, to potok deistvuet na disk s siloi

$F_\parallel = (p_k-p_0) \pi r^2 =\frac{1}{2} \rho v_0^2 S.$

(4.38)

Gidrodinamicheskaya sila $F_\parallel$ , kotoraya mozhet traktovat'sya kak sila lobovogo soprotivleniya pri dvizhenii diska so skorost'yu v₀ v zhidkosti, i vdvoe men'she sily, vychislyaemoi na osnove udarnoi teorii (sm. (4.36) pri $\sin\alpha$ ). Esli teper' v potok pomestit' shar, to po udarnoi teorii na nego budet deistvovat' ta zhe sila, chto i na disk. Pri gidrodinamicheskom podhode eta sila budet otsutstvovat' vovse. Deistvitel'no, pri simmetrichnom potoke otnositel'no secheniya O₁O₂ davlenie v proizvol'noi t.M i simmetrichnoi t.M' budut odinakovy, poskol'ku odinakovy skorosti potoka v etih tochkah. Ravenstvo nulyu rezul'tiruyushei sily pri plavnom (bezotryvnom) obtekanii ideal'noi zhidkost'yu shara, cilindra i dr. Nazyvaetsya paradoksom Dalambera. Davlenie v lyuboi tochke potoka vblizi poverhnosti shara mozhno rasschitat', pol'zuyas' uravneniem Bernulli:

$p=p_0 + \frac{\rho v_0^2 }{2} - \frac{\rho v^2 }{2}.$

(4.39)

Na ris. 4.20 izobrazheno raspredelenie izbytochnyh sil davleniya $\sigma_p=p-p_0$ , deistvuyushih normal'no na edinicu ploshadi poverhnosti shara. Pri etom sila napravlena k poverhnosti, esli p>p₀, i ot poverhnosti pri p<p₀. Otsutstvie sily v t.A i t.A' est' rezul'tat ravenstva skorostei v etih tochkah ishodnoi skorosti potoka: v_A=v'_A=v₀.

Ris. 4.20.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce