Astronet > Mehanika sploshnyh sred

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika sploshnyh sred

Telo v potoke vyazkoi zhidkosti. Lobovoe soprotivlenie.

Iz povsednevnoi praktiki izvestno, chto potok real'noi zhidkosti gaza deistvuet s nekotoroi siloi na telo, pomeshennoe v etot potok. Dlya osesimmetrichnogo tela s os'yu simmetrii, napravlennoi vdol' potoka, eta sila takzhe budet napravlena vdol' potoka. Ona poluchila nazvanie sily lobovogo soprotivleniya. Eta sila vozrastaet s uvelicheniem skorosti potoka podobno vozrastaniyu perepada davlenii pri uvelichenii skorosti techeniya zhidkosti po trube (sm. ris. 4.12). Osnovnye fizicheskie prichiny vozniknoveniya lobovogo soprotivleniya mozhno ustanovit' naibolee prosto, esli rassmotret' obtekanie potokom shara radiusa r. Na ris. 4.21. izobrazhena sila lobovogo soprotivleniya kak funkciya chisla Reinol'dsa ${\rm Re}= \frac{\rho v r}{\mu}$ . Pri malyh skorostyah dvizheniya, kogda ${\rm Re}\le 10^2, F_\parallel \sim v$ . Eto proishodit potomu, chto na sharik deistvuyut sily vyazkosti, voznikayushie iz-za sushestvovaniya tonkogo pogranichnogo sloya vblizi poverhnosti shara. Pri takih skorostyah v sloe proishodit laminarnoe (sloistoe) techenie zhidkosti. V nastoyashee vremya horosho razvita teoriya pogranichnogo sloya, kotoraya, v chastnosti, pozvolyaet ocenit' ego velichinu po formule

$\delta\cong \frac{r}{\sqrt{{\rm Re}}}.$

(4.40)

V konce lineinogo uchastka krivoi (ris. 4.21), gde Re $\cong$ 10², tolshina pogranichnogo sloya s laminarnym techeniem na poryadok men'she radiusa shara. Vne etogo sloya real'naya zhidkost' techet tak zhe, kak i ideal'naya, simmetrichno speredi i szadi obtekaya shar.

Ris. 4.21.

Naoborot, pri chislah Re~1 govorit' o pogranichnom sloe nekorrektno, t.k. gradienty skorosti prisutstvuyut v okruzhayushem prostranstve, po razmeru znachitel'no bol'shem radiusa shara. Takaya situaciya, naprimer, imela mesto pri vyazkom techenii zhidkosti po trubam pri Re $\le$ 1. Togda gradienty skorosti (i sily vyazkosti) byli raspredeleny po vsem secheniyam truby (sm. f-lu Puazeilya). Pri malyh chislah Reinol'dsa sila lobovogo soprotivleniya podchinyaetsya zakonu Stoksa:

$F_\parallel= 6\pi\mu rv.$

(4.41)

Kak uzhe upominalos' vyshe, mozhno izmerit' vyazkost' zhidkosti, nablyudaya dvizhenie v nei tel. Tak, pri padenii sharika v zhidkosti, ego skorost' izmenyaetsya v sootvetstvii s uravneniem:

$m\frac{dv}{dt}= mg - F_A - F_\parallel.$

(4.42)

Zdes' m - massa sharika, F_A - vytalkivayushaya sila i $F_\parallel$ - sila vyazkogo treniya, davaemaya formuloi (4.41). Po istechenii nekotorogo promezhutka vremeni sharik priobretet nekotoruyu maksimal'nuyu skorost', s kotoroi on prakticheski ravnomerno budet padat' vniz. Legko podschitat' etu skorost', polozhiv summu sil v pravoi chasti (4.42) ravnoi nulyu:

$\frac{4}{3}\pi r^3 (\rho_sh-\rho_zh)-6\pi\mu rv =0.$

(4.43)

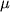
V eksperimente mozhno snachala izmerit' skorost' padayushego sharika i, pol'zuyas' (4.43), opredelit' vyazkost' zhidkosti $\mu$ . Tak, naprimer, skorost' padeniya stal'nogo sharika r=1 mm v vyazkom glicerine pri 40 $^\circ C$ v $\approx$ 0.5 sm/s, i vyazkost' $\mu\approx 0.3 {\rm kg/(m\cdot s}$ . Etoi skorosti sootvetstvuet chislo Reinol'dsa Re $\approx$ 0.02, poetomu zdes' otsutstvuet pogranichnyi sloi. Pri skorostyah potoka, kogda Re>10² simmetriya obtekaniya narushaetsya - pozadi shara proishodit otryv linii toka (ris. 4.22).

Ris. 4.22.

Pri takih skorostyah pogranichnyi sloi stanovitsya ochen' tonkim, a poperechnye gradienty skorosti v nem - bol'shimi. Sily vyazkosti, kotorye pri etom vozrastayut, tormozyat dvizhenie chastic vozduha, dvizhushihsya vdol' poverhnosti shara nastol'ko (propusheno slovo), chto oni ne v sostoyanii obognut' polnost'yu shar s obratnoi storony. Hotya techenie v tonkom pogranichnom sloe ostaetsya laminarnym, pozadi shara obrazuetsya zavihrennoe prostranstvo. Simmetriya davleniya v t.A i v t.A' narushaetsya. Speredi shara techenie takoe, kak i v otsutstvie treniya, poetomu davlenie v t. K $p_k=p_0 + \rho v^2 / 2$ . Odnako v tochke . Poetomu rezul'tiruyushaya sila davleniya, deistvuyushaya na shar v napravlenii potoka, budet proporcional'na dinamicheskomu naporu $\rho v^2 / 2$ i ploshadi poperechnogo secheniya shara $S=\pi r^2$ . Na praktike silu lobovogo soprotivleniya zapisyvayut v vide

$F_\parallel = C_X\cdot S\frac{\rho v^2 }{2},$

(4.44)

gde C_X - koefficient lobovogo soprotivleniya tela dannoi formy. Oblast' kvadratichnoi zavisimosti sily $F_\parallel$ ot skorosti v prostiraetsya vplot' do chisel Reinol'dsa Re~10⁵. Pri bol'shih skorostyah postepenno turbuliziruetsya pogranichnyi sloi i pri Re=3*10⁵ pogranichnyi sloi polnost'yu turbulenten. V oblasti postepennoi turbulizacii pogranichnogo sloya sila soprotivleniya s rostom skorosti dazhe umen'shaetsya, poskol'ku sokrashaetsya oblast' sryva potoka. Odnako zatem kvadratichnaya zavisimost' (4.44) opyat' vosstanavlivaetsya, pravda, s neskol'ko men'shim koefficientom C_X.

Ris. 4.23.

Kak my delali eto i ran'she, dlya laminarnogo i turbulentnogo obtekaniya tel mozhno ispol'zovat' edinuyu formulu dlya rascheta sily lobovogo soprotivleniya

$F_\parallel = C_X({\rm Re})\cdot S\cdot \frac{\rho v^2 }{2},$

(4.45)

v kotoroi koefficient lobovogo soprotivleniya dolzhen zaviset' ot skorosti tak, kak eto izobrazheno na ris. 4.23. Po svoemu vidu eta zavisimost' ochen' pohozha na zavisimost' bezrazmernogo gidravlicheskogo koefficienta ot chisla Re(sm. vyshe). Horoshei illyustraciei k vozniknoveniyu sily lobovogo soprotivleniya iz-za nesimmetrichnogo obtekaniya tela sluzhat predstavlennye v tablice velichiny koefficientov lobovogo soprotivleniya tel razlichnoi formy.

	telo	S_x
	disk	1,11
	polusfera	1,35...1,40
	polusfera	0,30...0,40
	shar	0,4
	kaplevidnoe	0,045
	kaplevidnoe	0,1

Horosho vidno, chto naimen'shim koefficientom lobovogo soprotivleniya obladaet osesimmetrichnoe kapleobraznoe telo, u kotorogo tupoi nos i zaostrennaya zadnyaya chast'. Pri obtekanii etogo tela potok horosho smykaetsya pozadi nego, prepyatstvuya, tem samym, padeniyu davleniya za telom.

Pod'emnaya sila. Formula Zhukovskogo.

Opyt pokazyvaet, chto pri obtekanii ideal'noi zhidkost'yu nesimmetrichnyh tel, da eshe proizvol'no orientirovannyh po napravleniyu k potoku, na eti tela budet deistvovat' sila F, napravlennaya pod nekotorym uglom k potoku (sm. ris. 4.18). Sostavlyayushaya etoi sily $F_\parallel$ , parallel'naya potoku, yavlyaetsya siloi lobovogo soprotivleniya. Drugaya sostavlyayushaya $F_\perp$ , napravlennaya poperek potoka, nosit nazvanie pod'emnoi sily. V kachestve vazhneishego primera rassmotrim vozniknovenie pod'emnoi sily pri obtekanii vozduhom kryla samoleta. 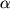Tipichnaya kartina bezotryvnogo obtekaniya vozduhom profilya kryla samoleta pri nebol'shom ugle ataki $\alpha$ izobrazhena na ris. 4.24a. Uzhe iz odnogo tol'ko fakta, chto potok posle obtekaniya priobrel sostavlyayushuyu impul'sa, napravlennuyu vniz, sleduet, chto takoi zhe impul's vverh priobretaet krylo. Dlya laminarnogo obtekaniya kryla ishodya iz struktury linii toka mozhno kachestvenno proanalizirovat' raspredelenie sil davleniya $\sigma_p=p-p_0$ , poluchaemoe s ispol'zovaniem uravneniya Bernulli (ris. 4.24b). Summa etih sil imeet ravnodeistvuyushuyu F, napravlennuyu pod nebol'shim uglom k vertikali. Takim obrazom, sozdaetsya pod'emnaya sila $F_\perp$ znachitel'no prevoshodyashaya silu lobovogo soprotivleniya.

Ris. 4.24.

Iz diagrammy sil davleniya vidno, chto pod'emnaya sila sozdaetsya ne stol'ko povysheniem davleniya pod krylom, skol'ko padeniem davleniya nad krylom. Eta sila proporcional'na dinamicheskomu davleniyu, ploshadi kryla S i vychislyaetsya po formule

$F_\perp =C_y S \frac{\rho v^2}{2},$

(4.46)

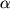
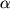
gde S_y - koefficient pod'emnoi sily, zavisyashii ot ugla ataki $\alpha$ . Esli by vozduh obtekal krylo bezotryvno, to koefficient S_y vozrastal by proporcional'no $\alpha$ . Odnako opyty pokazyvayut, chto pri uglah ataki $\alpha=12^\circ \div 18^\circ$ (v zavisimosti ot formy kryla) pod'emnaya sila dostigaet maksimuma, a zatem nachinaet padat' (ris. 4.25).

Ris. 4.25.

Ugol ataki, pri kotorom koefficient S_y maksimalen, nazyvaetsya posadochnym ili kriticheskim, a sootvetstvuyushii koefficient takzhe nazyvaetsya posadochnym. U obychnyh kryl'ev $S_{y_{pos}}= 1,2 \div 1,6$ . Na ris. 4.26 predstavleny fotografii potokov pri uglah ataki $\alpha<\alpha_{pos}$ i $\alpha>\alpha_{pos}$ . Horosho vidno, chto sryv potoka i obrazovanie zavihreniya privodit k povysheniyu davleniya nad krylom i umen'sheniyu pod'emnoi sily.

Ris. 4.26.

Koefficient $S_{y_{pos}}$ opredelyaet posadochnuyu skorost' samoleta v_pos, opredelyaemuyu iz ravenstva pod'emnoi sily (4.46) vesu samoleta. Dlya snizheniya skorosti posadki neobhodimo predotvratit' sryv potoka pri uvelichenii ugla ataki. V sovremennoi aviacii etogo dobivayutsya primeneniem na kryl'yah posadochnyh prisposoblenii - podkrylkov (1) i zakrylkov (2), vydvigaemyh mehanicheski iz kryla (3) pri posadke samoleta (ris. 4.27).

Ris. 4.27.

Vydayushayasya rol' v razrabotke teorii obtekaniya tel potokom, sygravshei isklyuchitel'no vazhnoe znachenie dlya razvitiya aviacii, prinadlezhit N.E. Zhukovskomu. On pokazal, chto pod'emnaya sila kryla svyazana s vihryami: okolo kryla sushestvuet vihr', nazvannyi im prisoedinennym. Osnovnaya ideya rascheta pod'emnoi sily svoditsya k sleduyushemu. Esli by v vozduhe otsutstvovali sily vyazkosti, to kartina obtekaniya kryla byla takoi, kak na ris. 4.28(a). Pod'emnaya sila, odnako, budet ravna nulyu, poskol'ku potok pozadi kryla ne izmenil napravleniya dvizheniya. Obtekanie kryla real'nym vozduhom, izobrazhennoe na ris. 4.28(v) mozhet rassmatrivat'sya kak superpoziciya nevyazkogo obtekaniya (a) i vihrevogo dvizheniya vozduha vokrug kryla samoleta po chasovoi strelke (b).

Ris. 4.28.

Velichina pod'emnoi sily napryamuyu svyazana s nalichiem cirkulyacii skorosti G (4.24) po konturu, ohvatyvayushemu krylo samoleta. Etot kontur dolzhen nahodit'sya vne pogranichnogo sloya (b), tolshina kotorogo dlya dvizhushegosya s dozvukovoi skorost'yu samoleta sostavlyaet neskol'ko santimetrov. Iz zakona sohraneniya momenta impul'sa sleduet, chto pozadi kryla dolzhny obrazovyvat'sya vihri s dvizheniem v nih vozduha protiv chasovoi strelki. Na ris. 4.29 predstavleny fotografii vihrevoi dorozhki, obrazuyusheisya pri obtekanii umen'shennoi modeli kryla samoleta.

Ris. 4.29.

Eta cepochka vihrei poyavlyaetsya potomu, chto pri otryve ot kryla odnogo vihrya cirkulyaciya vokrug kryla G iz-za vyazkosti postoyanno umen'shaetsya. Potok stremitsya vernut'sya k konfiguracii (a) na ris. 4.28, pri kotoroi chasticy vozduha "norovyat" obognut' "snizu-vverh" zadnyuyu kromku kryla. A eto v svoyu ochered' privedet k obrazovaniyu novogo vihrya i poyavleniyu cirkulyacii G vokrug kryla. Pri polete samoleta vihri periodicheski otryvayutsya ot kryla i unosyatsya potokom vozduha. Takim obrazom, vyazkost' sposobstvuet formirovaniyu obtekaniya kryla, sootvetstvuyushego situacii (v). Raschet zhe pod'emnoi sily mozhet byt' proveden na osnove rezul'tiruyushei sil davleniya, ishodya iz teorii techeniya ideal'noi zhidkosti. Raspredelenie davlenii vblizi pogranichnogo sloya svyazano so skorost'yu potoka formuloi:

$p=p_0 + \frac{\rho v_0^2 }{2} - \frac{\rho v^2 }{2}.$

(4.47)

Sila, deistvuyushaya na element poverhnosti kryla dlinoi L ravna

$dF= (p_n - p_v) L d\ell.$

(4.48)

i zavisit ot raznosti davlenii snizu i sverhu elementa kryla (ris. 4.30). Eta raznost' davlenii mozhet byt' vyrazhena s pomosh'yu (4.47) cherez skorosti:

$p_n - p_v=\frac{1}{2}\rho (v_v^2 - v_n^2 ) =\frac{1}{2}\rho (v_v - v_n ) (v_v + v_n ) .$

(4.49)

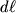
Skorosti v_n v_v berutsya v simmetrichnyh tochkah otnositel'no hordy kryla dlinoi b (naibol'shego rasstoyaniya mezhdu perednei i zadnei kromkoi kryla), element dliny $d\ell$ v formule (4.48) - eto element dliny hordy, poskol'ku sila dF napravlena perpendikulyarno horde. Podstavlyaya (4.49) v (4.47) v priblizhenii, chto v_n+v_v $\approx$ 2v i vypolnyaya integrirovanie, nahodim polnuyu silu:

$F_\perp=\int dF= \rho v L \int\limits_0^b (v_v - v_n ) d\ell =\rho v L \Gamma.$

(4.50)

Eta formula poluchena N.E. Zhukovskim i nosit ego imya. Cirkulyaciya G, opredelyayushaya pod'emnuyu silu, proporcional'na uglu ataki i dlya ploskogo kryla

$\Gamma=\frac{1}{2}\pi bv\alpha.$

(4.48)

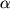
Dlya profil'nogo kryla, izobrazhennogo na ris. (4.30) pod'emnaya sila sushestvuet i pri nulevom ugle ataki ( $\alpha$ =0) i ischezaet, kogda ugol ataki dostigaet nekotoroi otricatel'noi velichiny.

Ris. 4.30.

Otmetim, chto pri uvelichenii ugla ataki rastet i lobovoe soprotivlenie. Otnoshenie poleznoi pod'emnoi sily k vrednoi sile lobovogo soprotivleniya opredelyaet "kachestvo kryla". Dlya legkih sportivnyh samoletov i istrebitelei eto kachestvo nahoditsya v predelah 12-15, a dlya tyazhelyh gruzovyh i passazhirskih samoletov ono dostigaet velichin 17-25. Aerodinamicheskoe kachestvo povyshaetsya pri uluchshenii obtekaemosti (umen'shenii S_x) i uvelichenii otnosheniya razmaha kryla L k dline ego hordy b. Iz diagrammy sil davleniya sleduet, chto ravnodeistvuyushaya etih sil smeshena k perednei kromke kryla. Eto neobhodimo prinimat' vo vnimanie pri opredelenii momentov sil, deistvuyushih na krylo, opredelyayushih ustoichivost' samoleta. Ves'ma pouchitel'nym yavlyaetsya opyt s tonkim diskom, nahodyashimsya v potoke vozduha. Esli struyu ot ventilyatora napravit' na disk, mogushii svobodno vrashat'sya vokrug vertikal'noi osi (ris. 4.31), to disk zaimet ustoichivoe polozhenie, kogda ego ploskost' stanet perpendikulyarna potoku vozduha. Esli disk sluchaino povernetsya, i kromka K₁ diska okazhetsya blizhe k ventilyatoru, chem kromka K₂, to vozniknet pod'emnaya sila, tochka prilozheniya kotoroi budet raspolozhena mezhdu kromkoi K₁ i os'yu vrasheniya diska. Moment etoi sily povernet disk v ishodnoe ustoichivoe polozhenie. Otmetim, chto polozhenie, pri kotorom ploskost' diska napravlena po potoku, yavlyaetsya takzhe polozheniem ravnovesiya, odnako eto ravnovesie yavlyaetsya neustoichivym.

Ris. 4.31.

Nazad | Vpered

Publikacii s klyuchevymi slovami: mehanika - gidrodinamika - gazodinamika - uprugost' Publikacii so slovami: mehanika - gidrodinamika - gazodinamika - uprugost'
Sm. takzhe: D'Alambera-Eilera paradoks Mehanika tverdogo tela. Lekcii. Chislo Maha Variacionnye principy mehaniki Konus Maha Bernulli uravnenie Barotropnoe yavlenie Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce