Fizicheskii vakuum i kosmicheskaya anti-gravitaciya

---

<< 3. Fizicheskii vakuum i ... | Oglavlenie | 5. Staticheskii mir >>

4. Anti-gravitaciya i uskoryayusheesya rasshirenie

V stat'e Ya.B. Zel'dovicha [17], opublikovannoi v uzhe upominavshemsya fridmanovskom vypuske Uspehov Fizicheskih Nauk za 1963 g. (togda otmechalos' sorokoletie teorii rasshiryayusheisya Vselennoi), ob'yasnyaetsya, kak dinamiku kosmologicheskogo rasshireniya mozhno naglyadno predstavit' na yazyke n'yutonovskoi mehaniki. Sushestvuet sposob rassuzhdenii, vpervye predlozhennyi E.A. Milnom i U.G. MakKri v nachale 1930-h godov, kotoryi pozvolyaet izbezhat' vseh (tochnee, pochti vseh) paradoksov n'yutonovskogo tyagoteniya, kotorye voznikayut pri popytke primenit' klassicheskuyu mehaniku k neogranichennomu, beskonechnomu v prostranstve raspredeleniyu tyagoteyushei massy; pri etom udaetsya poluchit' rezul'tat, kotoryi v tochnosti sovpadaet s tem, chto daet relyativistskaya teoriya Fridmana. Okazyvaetsya, chto o beskonechnosti mozhno zabyt', esli rassmotret' shar konechnyh razmerov, myslenno vydelennyi iz obshego odnorodnogo raspredeleniya veshestva. Na dinamiku shara vneshnie sloi veshestva ne vliyayut, tak kak oni sfericheski-simmetrichny, a vnutrennyaya massa shara deistvuet na tochku na ego poverhnosti tak, kak esli by vsya eta massa byla sosredotochena v centre shara. Togda zakon obratnyh kvadratov daet uravnenie dvizheniya dlya chasticy na poverhnosti shara:

Zdes' - radius shara, - ego polnaya gravitiruyushaya massa:

Vospol'zuemsya etim priemom chtoby pokazat' rol' vakuuma v dinamike kosmologicheskogo rasshireniya. Esli v polnuyu gravitiruyushuyu plotnost' shara vklyuchit' plotnosti vseh chetyreh nazvannyh vyshe komponent kosmicheskoi sredy, to poluchim

gde gravitacionnyi effekt davleniya (kotoryi otsutstvuet v n'yutonovskom tyagotenii, no dolzhet byt', konechno, prinyat vo vnimanie v nashem rassmotrenii) uchten kak dlya vakuuma, tak i dlya izlucheniya s ego uravneniem sostoyaniya .

V kosmologicheskoi modeli Einshteina imeetsya tol'ko vakuum i nerelyativistskoe veshestvo s plotnost'yu ; poetomu v takoi modeli . Mir Einshteina statichen, tak kak effektivnaya gravitiruyushaya plotnost' schitaetsya v etoi modeli ravnoi nulyu. Iz usloviya vytekaet svyaz' mezhdu plotnostyami, , chto i opisyvaet balans gravitacii veshestva i anti-gravitacii vakuuma. V etom sluchae sila i uskorenie v uravnenii dvizheniya (6) dlya shara ravny nulyu, i dlya neizmennosti ego radiusa ostaetsya tol'ko potrebovat', chtoby i skorost' chastic shara ravnyalas' nulyu. V modeli Fridmana eti usloviya neobyazatel'ny; otsyuda - vozmozhnost' dinamiki i evolyucii, shar mozhet, voobshe govorya, szhimat'sya ili rasshiryat'sya.

Pri adiabaticheskom szhatii ili rasshirenii odnorodnogo shara svyaz' mezhdu izmeneniem plotnosti i davleniem opisyvaetsya uravneniem

dlya lyuboi komponenty sredy, esli mezhdu komponentami net obmena energiei. Kak legko proverit', eto sootnoshenie vytekaet iz termodinamicheskogo tozhdestva (gde, kak obychno, - polnaya vnutrenyaya energiya (schitaya s energiei pokoya), temperatura veshestva i ego entropiya v ob'eme ), esli schitat', chto . Iz uravneniya (9) legko naiti, kak plotnosti veshestva i izlucheniya izmenyayutsya so vremenem pri izmenenii ego radiusa v hode rasshireniya ili szhatiya shara:

Zdes' tri velichiny - proizvol'nye postoyannye integrirovaniya. To zhe termodinamicheskoe uravnenie (9) lishnii raz ukazyvet, chto vakuum pri ego uravnenii sostoyaniya dolzhen imet' postoyannuyu vo vremeni plotnost': .

Esli podstavit' sootnosheniya (8,10) v uravnenie dvizheniya (6), to poslednee mozhno odin raz prointegrirovat' po vremeni:

Zdes' - proizvol'naya konstanta integrirovaniya; tochnee, eto velichina ne zavisit ot vremeni, no yavlyaetsya funkciei polnoi massy shara. Radius shara i sam, ochevidno, zavisit ot massy shara; radius igraet rol' eilerovoi koordinaty dlya chasticy, nahodyasheisya na poverhnosti shara, a massa barionov shara, kotoraya ne menyaetsya so vremenem dlya dannoi chasticy, sluzhit ee lagranzhevoi koordinatoi. Vhodyashie v poslednee sootnoshenie konstanty dayutsya obshim sootnosheniem

v kotorom dlya kazhdoi komponenty kosmicheskoi sredy. Dlya vakuuma , dlya temnogo veshestva i barionov , dlya izlucheniya ; . Esli dlya kakogo-to znacheniya izvestny sootvetstvuyushie znacheniya plotnostei, konstanty mogut byt' naideny. Eti integraly sluzhat, takim obrazom, dlya zadaniya nachal'nyh uslovii v teorii Fridmana. Kak vidno iz (12), integraly dlya raznyh uravnenii sostoyaniya imeyut odinakovuyu razmernost' (dliny). Ih chislennye znacheniya blizki drug k drugu po poryadku velichiny i sostavlyayut sm (sm. dalee).

Integral dlya veshestva bez davleniya poyavilsya (i byl oboznachen takim obrazom) v pervoi kosmologicheskoi rabote Fridmana [5] - sm. formulu (8) etoi klassicheskoi stat'i. Budem nazyvat' integraly (12) dlya razlichnyh form kosmicheskoi energii fridmanovskimi integralami.

Kak vsegda, pervyi integral uravnenii dvizheniya est' energiya, i velichina v (11) - eto polnaya mehanicheskaya energiya chasticy v raschete na edinicu massy. Kineticheskaya energiya stoit v levoi chasti uravneniya (12), a potencial'naya energiya (obe eti energii tozhe otnosyatsya k edinichnoi masse) - eto vzyataya s protivopolozhnym znakom summa pervyh chetyreh slagaemyh v pravoi chasti etogo uravneniya. Polnaya energiya mozhet byt' polozhitel'noi, otricatel'noi ili ravnoi nulyu; sootvetstvuyushie tipy dvizheniya obychno nazyvayut giperbolicheskim, ellipticheskim i parabolicheskim.

Zamechatel'no, chto vo fridmanovskii kosmologii dinamika rasshiryayusheisya Vselennoi daetsya uravneniem tochno togo zhe vida, chto i n'yutonovskii zakon sohraneniya energii (11):

V teorii Fridmana - masshtabnyi faktor, proporcional'no kotoromu izmenyayutsya vse rasstoyaniya v rasshiryayushemsya mire; dlya modelei nenulevoi prostranstvennoi krivizny eta velichina sluzhit i radiusom krivizny trehmernogo prostranstva. Znak krivizny v (13), (dlya zakrytoi, ploskoi i otkrytoi modelei, sootvetstvenno), protivopolozhen znaku polnoi energii v n'yutonovskom analoge fridmanovskogo uravneniya. Imeetsya, takim obrazom, vzaimno-odnaznachnaya svyaz' mezhdu kriviznoi prostranstva i dinamicheskim tipom kosmologicheskogo rasshireniya.

Tochnoe podobie relyativistskogo i n'yutonovskogo uravnenii ne prostaya sluchainost'; eto ochevidnoe proyavlenie v dannom sluchae odnogo iz osnovnyh principov teoreticheskoi fiziki, principa sootvetstviya, soglasno kotoromu novaya bolee obshaya teoriya vklyuchaet v sebya v kachestve predel'nogo ili chastnogo sluchaya staruyu teoriyu v oblasti ee primenimosti. Mozhno schitat', chto n'yutonovskie uravneniya dlya odnorodnogo shara primenyayutsya pri uslovii, chto skorost' rasshireniya shara gorazdo men'she skorosti sveta, a gravitacionnyi potencial na poverhnosti shara gorazdo men'she skorosti sveta v kvadrate. Eti usloviya opredelenno vypolnyayutsya dlya shara dostatochno malogo radiusa. No v mire Fridmana vse rasstoyaniya, schitaya i malye, izmenyayutsya proporcional'no masshtabnomu faktoru ; sledovatel'no i dlya malogo shara . Otsyuda i vytekaet neobhodimost' tochnogo podobiya uravnenii dlya i dlya kak funkcii vremeni. Dalee v formulah (9)-(11) budem podrazumevat' pod stoyashem tam .

(Stoit zametit', chto pri n'yutonovskom opisanii kosmologicheskogo rasshireniya bez paradoksov vse zhe ne obhoditsya. Deistvitel'no, uravnenie dvizheniya (6) zapisano, kak nuzhno schitat', v inercial'noi sisteme otscheta. V etoi sisteme chastica, nahodyashayasya v centre rassmatrivaemogo shara, pokoitsya; s neyu svyazano nachalo koordinat. No v odnorodnom mire vse bez isklyucheniya chasticy ravnopravny, i znachit, tochno takoe zhe uravnenie dvizheniya mozhno zapisat' i v sisteme otscheta, svyazannoi s chasticei, kotoraya nahoditsya, naprimer, na poverhnosti togo zhe shara. Odnako chastica na poverhnosti shara dvizhetsya otnositel'no ego centra otnyud' ne ravnomerno, a soglasno uravneniyu (6), s otlichnym ot nulya uskoreniem. Poetomu obe sistemy otscheta ne mogut byt' odnovremenno inercial'nymi. Etot paradoks snimaetsya v obshei teorii otnositel'nosti, gde ravnopravny vse svobodno padayushie sistemy otscheta, t.e. sistemy otscheta, kotorye opirayutsya na fizicheskie tela, besprepyatstvenno dvizhushiesya v pole tyazhesti.)

Iz uravnenii (11,13) mozhno videt', chto dinamicheskaya rol' vakuuma razlichna na raznyh etapah kosmologicheskogo rasshireniya. Na rannih etapah, pri malyh ili (formal'no pri ) slagaemoe v pravoi chasti oboih uravnenii, kotoroe opisyvaet vakuum, dolzhno byt' men'she chetyreh drugih slagaemyh ( ). Znachit, na etih etapah rasshireniya vliyanie vakuuma nesushestvenno. V takom sluchae mozhno prointegrirovat' uravneniya (11,13) v prenebrezhenii vakuumom (sm., naprimer, [18]) i tem samym naiti reshenie zadachi pri uslovii dinamicheskogo dominirovaniya obychnogo veshestva i izlucheniya. Tak kak tyagotenie obychnogo veshestva i izlucheniya sozdaet otricatel'noe uskorenie, , kosmologicheskoe rasshirenie proishodit s zamedleniem na etih rannih etapah evolyucii mira.

Pri bol'shih vremenah rol' vakuuma stanovitsya sushestvennoi, i, kak sleduet iz uravnenii (11,13), rano ili pozdno nastupaet etap dinamicheskogo preobladaniya vakuuma, kogda vakuumnoe slagaemoe v pravoi chasti etih uravnenii okazyvaetsya mnogo bol'she treh drugih slagaemyh sprava, opisyvayushih ne-vakuumnye komponenty kosmicheskoi sredy. V etom predel'nom sluchae bol'shih vremen (formal'no pri ) tyagoteniem ne-vakuumnyh komponent mozhno prenebrech', i reshenie uravnenii (11,13) imeet vid:

dlya , sootvetstvenno. Zdes', kak i vyshe, sm est' fridmanovskii integral dlya vakuuma, poluchayushiisya iz obshego sootnosheniya (12) pri . Integral okazyvaetsya postoyannym koefficientom reshenii dlya ; estestvenno takzhe vybrat' ego i dlya normirovki masshtabnogo faktora pri .

Tak kak vakuum s polozhitel'noi plotnost'yu sozdaet effektivnuyu anti-gravitaciyu (ego effektivnaya gravitiruyushaya plotnost' , kak my uzhe ne raz govorili), uskorenie okazyvaetsya polozhitel'nym, kogda v dinamike rasshireniya dominiruet vakuum, i reshenie (14) opisyvaet kosmologicheskoe rasshirenie, kotoroe uskoryaetsya so vremenem. Dlya vseh treh variantov modeli Fridmana, otvechayushih trem tipam dinamiki, kosmologicheskoe rasshirenie prodolzhaetsya, soglasno (14), neogranichenno dolgo. V predele bol'shih vremen rasshirenie proishodit po eksponencial'nomu zakonu dlya vseh treh variantov.

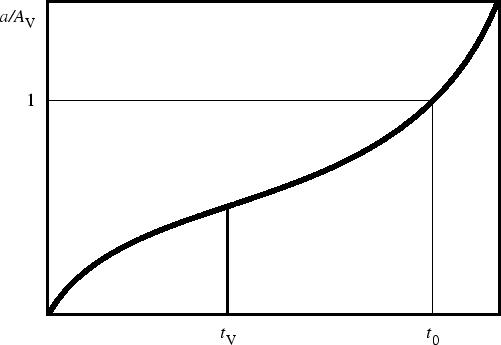
Smena zamedleniya uskoreniem i perehod k dominirovaniyu vakuuma v dinamike kosmologicheskogo rasshireniya sootvetstvuet ravenstvu plotnostei , kotoroe imeet, ochevidno, tot zhe smysl, chto i v staticheskoi modeli Einshteina. No v modeli Fridmana eto ravenstvo vozmozhno tol'ko v odin moment vremeni, i v etot edinstvennyi moment uskorenie obrashaetsya v nul'. Sootvetstvuyushee krasnoe smeshenie

Zdes' - sovremennyi vozrast mira; chislennoe znachenie krasnogo smesheniya dano dlya nablyudaemyh plotnostei (2-5).

Kak my govorili, effekt kosmologicheskogo uskoreniya, otkrytyi v nablyudeniyah sverhnovyh, proyavlyaetsya v zavisimosti ih bleska ot krasnogo smesheniya dlya bol'shih krasnyh smeshenii, - bol'shih, no ne prevyshayushih , kak i dolzhno byt', poskol'ku v bolee rannie vremena rasshirenie ne uskoryalos', a eshe zamedlyalos'.

V kosmologicheskom reshenii (14) habblovskaya postoyannaya est' , prakticheski dlya lyubogo vskore posle perehoda k dominirovaniyu vakuuma. Na stadii polnogo preobladniya vakuuma postoyannaya Habbla ne zavisit ot vremeni i opredelyaetsya tol'ko znacheniem plotnosti kosmicheskogo vakuuma. Legko proverit', chto eta svyaz' postoyannoi Habbla i plotnosti vakuuma soglasuetsya s izmerennymi znacheniyami etih velichin (v predelah oshibki izmerenii), - sm. dannye, privedennye v p.2. Sushestvenno, chto rech' zdes' idet o dvuh nezavisimyh tipah kosmologicheskih izmerenii.

Ostaetsya teper' zapisat' reshenie fridmanovskogo kosmologicheskogo uravneniya (13) dlya vseh vremen:

Zdes' prinyat znak plyus pered kornem kvadratnym, tak kak rassmatrivaetsya rasshirenie, a ne szhatie kosmicheskoi sredy; v kachestve nachala otscheta vremeni prinyat moment, kogda . Reshenie (16) predstavleno graficheski na Ris.1, postroennom v sootvetstvii s dannymi o postoyannoi Habbla i o plotnostyah vakuuma, temnogo veshestva, barionov i izlucheniya, privedennymi v (2-5). Kosmologicheskoe rasshirenie stanovitsya uskoryayushimsya pri mlrd let; sovremennyi vozrast mira mlrd let. V sovremennuyu epohu sm. Poslednee priblizhennoe sootnoshenie oznachaet sovpadenie rastushei so vremenem velichiny s postoyannoi dlinoi ; eto odno iz kosmicheskih sovpadenii, harakterizuyushih sovremennuyu epohu, i kak budet pokazano dalee, ono sushestvenno takzhe dlya ponimaniya drugih kosmicheskih sovpadenii.

Interesno, chto v oboih predel'nyh sluchayah, pri i pri , dinamika kosmologicheskogo rasshireniya ne zavisit ot znaka polnoi energii ili znaka prostranstvennoi krivizny , kak eto vidno iz uravneniya (16). Dlya vseh treh variantov dinamiki i krivizny rasshirenie nachinaetsya v parabolicheskom rezhime; zatem v techenie konechnogo vremeni mozhet proyavit'sya vozmozhnoe otlichie dinamiki rasshireniya ot etogo rezhima, a posle etogo rasshirenie vnov' vyhodit na parabolicheskii rezhim i sohranyaet etot tip dvizheniya neogranichenno dolgo.

Legko videt', chto vozmozhnye otlichiya ot parabolichnosti v deistvitel'nosti neveliki pri znacheniyah plotnostei (2)-(5). V sootvetstvii s fridmanovskoi teoriei, poslednee oznachaet, chto otkloneniya ot ploskoi geometrii 3-prostranstva tozhe ne mogut byt' bol'shimi v real'nom mire. Tem samym v obnovlennoi standartnoi kosmologii sama soboi reshaetsya tak naz. problema ploskostnosti, kotoruyu eshe nedavno rassmatrivali kak ser'eznuyu trudnost' etoi nauki.

---

<< 3. Fizicheskii vakuum i ... | Oglavlenie | 5. Staticheskii mir >>

Publikacii s klyuchevymi slovami: Kosmologiya - kosmomikrofizika - vakuum - Rasshirenie Vselennoi - kvantovaya gravitaciya - antigravitaciya - lyambda-chlen - Obshaya teoriya otnositel'nosti Publikacii so slovami: Kosmologiya - kosmomikrofizika - vakuum - Rasshirenie Vselennoi - kvantovaya gravitaciya - antigravitaciya - lyambda-chlen - Obshaya teoriya otnositel'nosti
Sm. takzhe: Razlozhenie dalekogo sveta Formirovanie galaktik v magnitnoi Vselennoi "Effekty" Zel'dovicha, zapechatlennye na nashem nebe Sverhnovaya 1994D i neozhidannaya Vselennaya Kuda smeshaetsya krasnoe smeshenie? Ne bogi rasshirenie vselennoi nablyudayut Samaya dalekaya sverhnovaya tipa Ia Vse publikacii na tu zhe temu >>