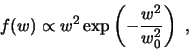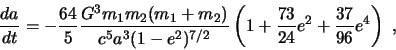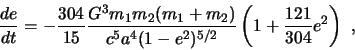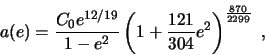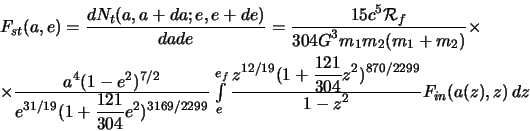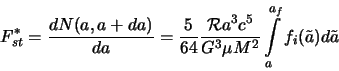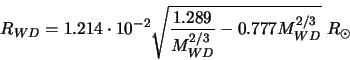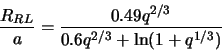Konkurs "Astronet-2001"
<< 1. Vvedenie | Oglavlenie | 3. GV ot kompaktnyh >>
- 2.1 Modelirovanie nachal'nyh uslovii metodom populyacionnogo sinteza
- 2.2 Stacionarnaya funkciya raspredeleniya kompaktnyh dvoinyh zvezd v Galaktike
2. Stacionarnaya funkciya raspredeleniya kompaktnyh dvoinyh zvezd v galaktike
2.1 Modelirovanie nachal'nyh uslovii metodom populyacionnogo sinteza
Sushestvovanie dvoinyh neitronnyh zvezd yavlyayutsya zakonomernym sledstviem evolyucii massivnyh dvoinyh zvezd. Izvestno shest' NZ v dvoinyh sistemah, vtorym komponentom kotoryh yavlyaetsya NZ.
| Dvoinye Pul'sary v parah s NZ | |||
| Sistemy | Period (dni) | ekscentrisitet, |
|
| B1913+16 | 0.323 | 0.617 |
|
| B1534+12 | 0.420 | 0.274 |
|
| B2721+11c | 0.335 | 0.681 |
|
| B2303+46 | 12.340 | 0.658 |
|
| J1518+4904 | 8.634 | 0.249 |
|
| B1820-11 |
357.762 | 0.795 |
|
|
|
|||
Tri iz etih sistem dostatochno tesnye dlya togo, chtoby slit'sya iz-za
ispuskaniya gravitacionnyh voln za vremya men'she Habblovskogo ![]() .
Teoreticheskaya ocenka tempa sliyaniya dvoinyh neitronnyh zvezd v Galaktike
.
Teoreticheskaya ocenka tempa sliyaniya dvoinyh neitronnyh zvezd v Galaktike ![]() sobytiya v god (sm. Grishuk i dr., 2001).
sobytiya v god (sm. Grishuk i dr., 2001).
Dvoinye sistemy obrazuyutsya s razlichnymi nachal'nymi parametrami
(massy komponent, bol'shaya poluos', ekscentrisitet).
Na evolyuciyu dvoinoi sistemy takzhe okazyvayut sil'noe vliyanie takie parametry, kak
dopolnitel'naya skorost' ![]() (skorost' «otdachi»),
priobretaemaya molodoi NZ vo vremya vspyshki sverhnovoi,
effektivnost' unosa uglovogo momenta na stadii obshei obolochki
(skorost' «otdachi»),
priobretaemaya molodoi NZ vo vremya vspyshki sverhnovoi,
effektivnost' unosa uglovogo momenta na stadii obshei obolochki ![]() i dr.
i dr.
Pri pomoshi metoda populyacionnogo sinteza ("Mashina scenariev", Lipunov i dr. 1996) provodilis'
raschety bol'shogo chisla evolyucionnyh trekov ![]() s razlichnymi nachal'nymi parametrami.
Chast' etih trekov privodila k obrazovaniyu dvoinyh neitronnyh zvezd.
Pri etom, v sisteme dvazhdy proishodila vspyshka sverhnovoi tipa II ili Ib/s (esli vodorodnaya
obolochka byla poteryana v hode obmena massami).
s razlichnymi nachal'nymi parametrami.
Chast' etih trekov privodila k obrazovaniyu dvoinyh neitronnyh zvezd.
Pri etom, v sisteme dvazhdy proishodila vspyshka sverhnovoi tipa II ili Ib/s (esli vodorodnaya
obolochka byla poteryana v hode obmena massami).
Pri mgnovennom sfericheski-simmetrichnom sbrose massy odnoi iz komponent dvoinoi
sistemy na krugovoi orbite novaya orbita stanovitsya elliptichnoi s ekscentrisitetom ![]() (Blaau 1961),
gde
(Blaau 1961),
gde ![]() - sbroshennaya massa,
- sbroshennaya massa, ![]() - polnaya massa sistemy posle vspyshki sverhnovoi.
Esli sushestvuet asimmetriya kollapsa, kotoraya harakterizuetsya dopolnitel'noi
prostranstvennoi skorost'yu, to
ekscentrisitety orbit obrazuyushihsya NZ v srednem stanovyatsya bol'she.
- polnaya massa sistemy posle vspyshki sverhnovoi.
Esli sushestvuet asimmetriya kollapsa, kotoraya harakterizuetsya dopolnitel'noi
prostranstvennoi skorost'yu, to
ekscentrisitety orbit obrazuyushihsya NZ v srednem stanovyatsya bol'she.
Kak uzhe govorilos' vyshe, dopolnitel'naya skorost',
kotoruyu priobretaet molodaya NZ, vliyaet na evolyuciyu dvoinoi sistemy
(raspad sistemy, izmenenie ekscentrisiteta, raspredelenie prostranstvennyh skorostei).
Nablyudatel'nye dannye po radiopul'saram pokazyvayut, chto raspredelenie dopolnitel'nyh
skorostei imeet srednee znachenie poryadka 200 - 400 km/s i obladaet shirokoi formoi
s vysokoskorostnym hvostom, tyanushimsya do skorostei poryadka 1500 km/s
(Lain i Lorimer 1994, Arzumanyan i dr. 2001).
Predpolagaem, chto raspredelenie skorosti «otdachi» imeet Maksvellovskuyu formu
Prostranstvennoe raspredelenie dvoinyh neitronnyh zvezd v Galaktike
yavlyaetsya ves'ma chuvstvitel'nym
k amplitude skorosti «otdachi» ![]() . Do vspyshki sverhnovoi dvoinaya sistema
nahoditsya v tonkom galakticheskom diske, gde rozhdayutsya zvezdy.
Posle dvuh (ili odnoi v sluchae sistem BK+NZ)
vspyshek sverhnovoi centr mass dvoinoi sistemy priobretaet znachitel'nuyu prostranstvennuyu
skorost', esli sistema ne raspalas' v rezul'tate vzryva.
Iz-za etogo obrazovavshayasya sistema NZ+NZ (BK+NZ)
mozhet uiti na bol'shie rasstoyaniya ot ploskosti galaktiki. Etot effekt rassmatrivalsya
v rabote Bulik i dr. 1999. Bylo pokazano, chto prostranstvennoe raspredelenie
dvoinyh neitronnyh zvezd pered sliyaniem imeet pochti sfericheskii vid i dlya
. Do vspyshki sverhnovoi dvoinaya sistema
nahoditsya v tonkom galakticheskom diske, gde rozhdayutsya zvezdy.
Posle dvuh (ili odnoi v sluchae sistem BK+NZ)
vspyshek sverhnovoi centr mass dvoinoi sistemy priobretaet znachitel'nuyu prostranstvennuyu
skorost', esli sistema ne raspalas' v rezul'tate vzryva.
Iz-za etogo obrazovavshayasya sistema NZ+NZ (BK+NZ)
mozhet uiti na bol'shie rasstoyaniya ot ploskosti galaktiki. Etot effekt rassmatrivalsya
v rabote Bulik i dr. 1999. Bylo pokazano, chto prostranstvennoe raspredelenie
dvoinyh neitronnyh zvezd pered sliyaniem imeet pochti sfericheskii vid i dlya ![]() km/s
tyanetsya do
km/s
tyanetsya do ![]() kpk. Dlya nahozhdeniya obratnogo srednego rasstoyaniya do kompaktnyh
dvoinyh zvezd v Galaktike my vospol'zovalis' rezul'tatami etoi raboty.
kpk. Dlya nahozhdeniya obratnogo srednego rasstoyaniya do kompaktnyh
dvoinyh zvezd v Galaktike my vospol'zovalis' rezul'tatami etoi raboty.
Tak kak interesuyushie nas detektory budut nahodit'sya v okrestnosti Solnca
(t.e. na rasstoyanii ![]() kpk ot centra Galaktiki), to neobhodimo znat'
prostranstvennoe raspredelenie dvoinyh NZ otnositel'no Solnca.
kpk ot centra Galaktiki), to neobhodimo znat'
prostranstvennoe raspredelenie dvoinyh NZ otnositel'no Solnca.
Mozhno svernut' amplitudu gravitacionnoi volny registriruemoi detektorom, kotoraya
obratno proporcional'na rasstoyaniyu do istochnika, s funkciei raspredeleniya rasstoyanii
ot Solnca do slivayushihsya sistem.
Predpolagaetsya, chto vse istochniki imeyut odinakovye massy,
v sluchae NZ
![]() (Prohorov i Postnov 2001); po vsem orbital'nym uglam provodim usrednenie.
Togda operaciyu svertki mozhem zamenit' opredeleniem
(Prohorov i Postnov 2001); po vsem orbital'nym uglam provodim usrednenie.
Togda operaciyu svertki mozhem zamenit' opredeleniem
![]() , i imenno
etu velichinu podstavit' vmesto neizvestnogo nam rasstoyaniya do istochnika.
Takzhe mozhno vvesti effektivnoe rasstoyanie
, i imenno
etu velichinu podstavit' vmesto neizvestnogo nam rasstoyaniya do istochnika.
Takzhe mozhno vvesti effektivnoe rasstoyanie
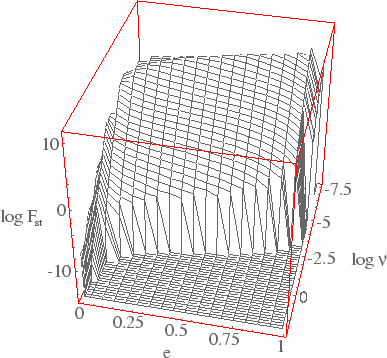
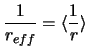 -
sootvetstvuyushee srednemu po ansamblyu obratnyh rasstoyanii do kompaktnyh dvoinyh zvezd.
V sluchae dvoinyh neitronnyh zvezd
-
sootvetstvuyushee srednemu po ansamblyu obratnyh rasstoyanii do kompaktnyh dvoinyh zvezd.
V sluchae dvoinyh neitronnyh zvezd ![]() kpk.
V sisteme massivnyi BK+NZ proishodit tol'ko odna vspyshka sverhnovoi i v srednem
prostranstvennaya skorost' centra mass sistemy men'she. Ocenim
kpk.
V sisteme massivnyi BK+NZ proishodit tol'ko odna vspyshka sverhnovoi i v srednem
prostranstvennaya skorost' centra mass sistemy men'she. Ocenim ![]() iz sleduyushih soobrazhenii: verhnii predel - eto
iz sleduyushih soobrazhenii: verhnii predel - eto
![]() kpk, a nizhnii predel -
eto rasstoyanie do centra Galaktiki. V kachestve ocenki voz'mem
kpk, a nizhnii predel -
eto rasstoyanie do centra Galaktiki. V kachestve ocenki voz'mem
![]() kpk.
kpk.
Dvoinye kompaktnye zvezdy formiruyutsya v shirokom intervale orbital'nyh parametrov:
bol'shoi poluosi ![]() i ekscentrisiteta
i ekscentrisiteta ![]() . Pri pomoshi programmy rascheta
evolyucii dvoinyh zvezd «Mashina Scenariev»
my poluchili nachal'nye funkcii raspredeleniya dvoinyh neitronnyh zvezd srazu posle
vtoroi vspyshki sverhnovoi i sistem sostoyashih iz massivnogo belogo karlika i
tol'ko chto obrazovannoi NZ po
. Pri pomoshi programmy rascheta
evolyucii dvoinyh zvezd «Mashina Scenariev»
my poluchili nachal'nye funkcii raspredeleniya dvoinyh neitronnyh zvezd srazu posle
vtoroi vspyshki sverhnovoi i sistem sostoyashih iz massivnogo belogo karlika i
tol'ko chto obrazovannoi NZ po ![]() .
Imenno eti parametry opredelyayut poteri energii i uglovogo momenta v vide GV
v dvoinoi sisteme.
.
Imenno eti parametry opredelyayut poteri energii i uglovogo momenta v vide GV
v dvoinoi sisteme.
 |
| Ris. 2.1
Nachal'naya funkciya raspredeleniya dvoinyh NZ |
Rassmotrim harakternye osobennosti nachal'noi funkcii raspredeleniya
sistem BK+BK.
Glavnoe otlichie ot dvoinyh neitronnyh zvezd sostoit v tom, chto
orbita sistemy sostoyashih iz dvuh belyh karlikov yavlyaetsya pochti
krugovoi, chto yavlyaetsya sledstviem prohozhdeniya etih sistem
stadii obshei obolochki.
Temp sliyaniya takih sistem
![]() god
god![]() .
.
Bolee interesnymi v etom plane predstavlyayutsya sistemy tipa BK+NZ,
v kotoroi pervichnaya komponenta v rezul'tate svoei evolyucii obrazuet belyi
karlik, a vtorichnaya komponenta vsledstvie peretekaniya veshestva s pervoi
zvezdy nabiraet neobhodimuyu massu i vzryvaetsya kak sverhnovaya.
Podrobnyi analiz obrazovaniya dvoinyh sistem, vklyuchayushih
staryi belyi karlik i moloduyu NZ, predstavitelyami
kotoryh mogut byt' radiopul'sary na ekscentrichnyh orbitah
PSR B2303+46 i PSR J1141-6545, provodilsya v rabote
Tauris i Sennels (2000), sm. takzhe Portegis Cvart i Yungel'son 1999
i Braun i dr. 2001.
Takaya sistema takzhe budet obladat'
otlichnym ot nulya ekscentrisitetom. No srednee znachenie ekscentrisiteta orbit
neveliko ![]() . Temp sliyaniya
. Temp sliyaniya
![]() god
god![]() .
Takim obrazom, hotya temp sliyaniya sistem BK+NZ sopostavim s tempom
sliyaniya NZ+NZ, eti sistemy imeyut v srednem men'shie ekscentrisitety
i my ne budem ih rassmatrivat' pri analize shirokopolosnyh
impul'sov GV ot slivayushihsya kompaktnyh dvoinyh zvezd (sm. razdel 3.3).
.
Takim obrazom, hotya temp sliyaniya sistem BK+NZ sopostavim s tempom
sliyaniya NZ+NZ, eti sistemy imeyut v srednem men'shie ekscentrisitety
i my ne budem ih rassmatrivat' pri analize shirokopolosnyh
impul'sov GV ot slivayushihsya kompaktnyh dvoinyh zvezd (sm. razdel 3.3).
2.2 Stacionarnaya funkciya raspredeleniya kompaktnyh dvoinyh zvezd v Galaktike
2.2.1 Postroenie stacionarnoi funkcii raspredeleniya
Posle obrazovaniya dvoinoi NZ dal'neishaya evolyuciya sistemy v osnovnom opredelyaetsya izlucheniem GV. Eto horoshee priblizhenie dlya dostatochno razrezhennyh zvezdnyh polei. V sluchae plotnyh zvezdnyh skoplenii sleduet uchityvat' processy dinamicheskogo vzaimodeistviya. Na poslednih stadiyah sliyaniya (poslednie «3 minuty»), a takzhe v sistemah tipa BK+NZ neobhodimo uchityvat' prilivnye vzaimodeistviya.
Budem predpolagat', chto evolyuciya sistemy opredelyaetsya tol'ko
odnim mehanizmom, a imenno izlucheniem GV, kotorye unosyat iz sistemy energiyu
i moment impul'sa. Takzhe predpolagaem, chto temp rozhdeniya takih sistem v Galaktike postoyanen
(razumnoe predpolozhenie dlya poslednih neskol'kih milliardov let). Pri
takih predpolozheniyah mozhno naiti stacionarnuyu funkciyu raspredeleniya
dvoinyh NZ po orbital'nym parametram ![]() v Galaktike. Dlya
takoi funkcii
v Galaktike. Dlya
takoi funkcii
![]() . Eto vypolnyaetsya, esli
harakternoe vremya sliyaniya dvoinoi sistemy bol'she harakternogo
vremeni izmeneniya parametrov nachal'noi funkcii raspredeleniya.
. Eto vypolnyaetsya, esli
harakternoe vremya sliyaniya dvoinoi sistemy bol'she harakternogo
vremeni izmeneniya parametrov nachal'noi funkcii raspredeleniya.
Vsledstvie izlucheniya GV bol'shaya poluos' ![]() i ekscentrisitet
i ekscentrisitet ![]() sistemy
budut umen'shat'sya s techeniem vremeni (Piterz i Mat'yuz 1963).
sistemy
budut umen'shat'sya s techeniem vremeni (Piterz i Mat'yuz 1963).
Na ploskosti ![]() sistema budet evolyucionirovat', dvigayas' po
evolyucionnomu treku (sm. risunok 2.2)
sistema budet evolyucionirovat', dvigayas' po
evolyucionnomu treku (sm. risunok 2.2)
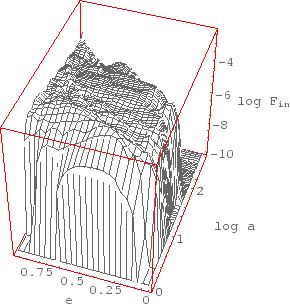
 |
| Ris. 2.2
Evolyucionnye treki dvoinyh sistem na fazovoi ploskosti |
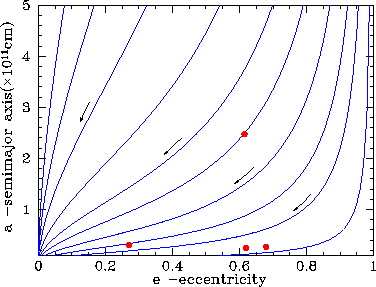
 |
| Ris. 2.3 Stacionarnaya funkciya raspredeleniya dvoinyh NZ na ellipticheskih orbitah slivayushihsya pod deistviem izlucheniya GV, rasschitannaya dlya nachal'noi funkcii raspredeleniya iz risunka 2.1. |
Togda, esli izvestna nachal'naya funkciya raspredeleniya, to mozhno postroit'
stacionarnuyu funkciyu raspredeleniya
(sm. Buitrago i dr. 1994, Pierro i Pinto 1996)
2.2.2 Osobennosti stacionarnoi funkcii raspredeleniya dlya dvoinyh sistem s belym karlikom
Podobnym obrazom mozhno postroit' stacionarnuyu funkciyu i dlya drugih tipov kompaktnyh sistem, znaya nachal'nuyu funkciyu raspredeleniya i predpolagaya, chto evolyuciya sistemy proishodit tol'ko iz-za izlucheniya GV.
V otlichie ot dvoinyh NZ, kotorye rozhdayutsya na orbitah s bol'shim ekscentrisitetom,
dvoinye BK rozhdayutsya na krugovyh orbitah. Eto znachitel'no uproshaet raschet
stacionarnoi funkcii raspredeleniya, poskol'ku v etom sluchae imeetsya
lish' odna nezavisimaya peremennaya ![]() .
Togda
.
Togda
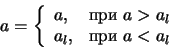
tak kak pri
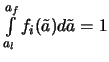 vsledstvie
vybrannoi normirovki.
V sluchae krugovyh orbit mozhno postroit' stacionarnuyu funkciyu raspredeleniya
dvoinyh kompaktnyh zvezd v oblasti
vsledstvie
vybrannoi normirovki.
V sluchae krugovyh orbit mozhno postroit' stacionarnuyu funkciyu raspredeleniya
dvoinyh kompaktnyh zvezd v oblasti Dlya sistem, hotya by odna iz komponent kotoryh belyi karlik, poyavlyaetsya eshe odno ogranichenie, svyazannoe s tem, chto v nekotoryi moment sblizheniya osnovnym processom, opredelyayushim evolyuciyu sistemy, stanovyatsya prilivnye vzaimodeistviya.
Ocenim etu granicu sleduyushim obrazom. Budem schitat', chto etot effekt
stanovitsya vazhen, kogda belyi karlik blizok k zapolneniyu svoei polosti Rosha,
t.e. polost' Rosha dlya belogo karlika v periastre budet poryadka 3 - 5
radiusov zvezdy.
gde
gde
Takim obrazom, iz usloviya (2.7) my poluchaem uslovie na minimal'noe
znachenie bol'shoi poluosi, kak funkciyu ekscentrisiteta i massy belogo
karlika.
<< 1. Vvedenie | Oglavlenie | 3. GV ot kompaktnyh >>
|
Publikacii s klyuchevymi slovami:
dvoinye zvezdy - gravitacionnoe izluchenie
Publikacii so slovami: dvoinye zvezdy - gravitacionnoe izluchenie | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |