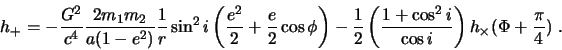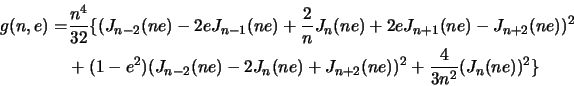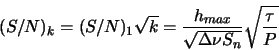Konkurs "Astronet-2001"
<< 2. Stacionarnaya funkciya raspredeleniya | Oglavlenie | 4. Obsuzhdenie >>
- 3.1 GV-izluchenie ot odnoi sistemy
- 3.2 Stohasticheskii GV-signal ot stacionarnogo ansamblya dvoinyh zvezd
- 3.3 Shirokopolosnyi GV-signal
3. GV ot kompaktnyh dvoinyh neitronnyh zvezd na ellipticheskih orbitah
3.1 GV-izluchenie ot odnoi sistemy
3.1.1 Sluchai nekrugovoi orbity
Rassmotrim GV-izluchenie ot dvoinoi sistemy, sostoyashei iz dvuh kompaktnyh zvezd s massami
Usrednyaya po orientacii orbity
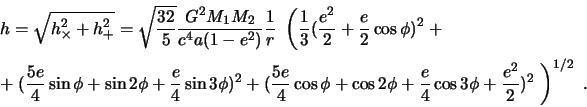 |
(3.3) |
V bolee prostom sluchae ![]() , amplituda GV ot istochnika, nahodyashegosya na rasstoyanii
, amplituda GV ot istochnika, nahodyashegosya na rasstoyanii ![]() ,
usrednennaya po orientacii orbity i periodu zapisyvaetsya v vide
,
usrednennaya po orientacii orbity i periodu zapisyvaetsya v vide
Pri izluchenii GV budut unosit' iz sistemy energiyu i impul's.
Energiya ![]() , perenosimaya GV v napravlenii ee rasprostraneniya
cherez ploshadku
, perenosimaya GV v napravlenii ee rasprostraneniya
cherez ploshadku ![]() za vremya
za vremya ![]()
Polnaya energiya, izluchaemaya otdel'nym istochnikom v edinicu vremeni nahoditsya integrirovaniem potoka (3.5) po vsem napravleniyam.
| (3.6) |
V spektral'nom predstavlenii, kolichestvo energii izluchaemoi v edinicu
vremeni na ![]() -garmonike (sm. Zel'dovich i Novikov 1967) mozhno zapisat'
-garmonike (sm. Zel'dovich i Novikov 1967) mozhno zapisat'
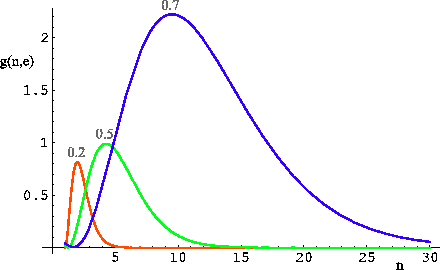 |
| Ris. 3.1
Funkciya |
3.1.2 Dlitel'nost' sliyaniya dvoinoi sistemy
Rassmotrim dvoinuyu sistemu na krugovoi orbite.
Takaya sistema teryaet gravitacionnuyu energiyu svyazi
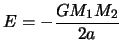 v vide
izlucheniya gravitacionnyh voln (3.7).
Pri etom poluos' orbity umen'shaetsya (v kvadrupol'nom priblizhenii) v sootvetstvii
s uravneniem.
v vide
izlucheniya gravitacionnyh voln (3.7).
Pri etom poluos' orbity umen'shaetsya (v kvadrupol'nom priblizhenii) v sootvetstvii
s uravneniem.
Eto vremya i est' dlitel'nost' sliyaniya dvoinoi sistemy.
V sluchae nekrugovoi orbity neobhodimo rassmatrivat' sistemu uravnenii (2.2)-(2.3). V rezul'tate poluchim
Vremya sliyaniya dvoinoi sistemy s nachal'nym ekscentrisitetom otlichnym ot nulya men'she,
chem dlya sistemy na krugovoi orbite s toi zhe nachal'noi poluos'yu ![]() .
.
Eto mozhet byt' ponyatno iz sleduyushih soobrazhenii.
V sluchae elliptichnoi orbity poteri energii iz-za izlucheniya GV bol'she, chem v sluchae
krugovoi orbity na faktor
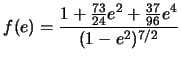 ,
kotoryi ochen' bystro rastet pri
,
kotoryi ochen' bystro rastet pri ![]() .
A gravitacionnaya energiya svyazi dvoinoi sistemy
zavisit tol'ko ot bol'shoi poluosi sistemy i ne zavisit ot ekscentrisiteta.
Izluchaya gravitacionnye volny, sistema stanovitsya bolee tesnoi i krugovoi
(
.
A gravitacionnaya energiya svyazi dvoinoi sistemy
zavisit tol'ko ot bol'shoi poluosi sistemy i ne zavisit ot ekscentrisiteta.
Izluchaya gravitacionnye volny, sistema stanovitsya bolee tesnoi i krugovoi
(
![]() i
i
![]() - imeyut otricatel'nyi znak).
Pri umen'shenie ekscentrisiteta umen'shaetsya i faktor
- imeyut otricatel'nyi znak).
Pri umen'shenie ekscentrisiteta umen'shaetsya i faktor ![]() , i k momentu
sliyaniya orbita stanovitsya pochti krugovoi. Umen'shenie faktora
, i k momentu
sliyaniya orbita stanovitsya pochti krugovoi. Umen'shenie faktora ![]() i
zavisimost'
i
zavisimost' ![]() opredelyaet integral (3.13).
opredelyaet integral (3.13).
3.2 Stohasticheskii GV-signal ot stacionarnogo ansamblya dvoinyh zvezd
Kak uzhe govorilos' vyshe, v Galaktike znachitel'naya chast' zvezd
vhodit v sostav dvoinyh sistem.
V sluchae bol'shogo chisla ![]() nezavisimyh odinakovyh istochnikov
na odnom i tom zhe rasstoyanii
nezavisimyh odinakovyh istochnikov
na odnom i tom zhe rasstoyanii ![]() , kotorye izluchayut
GV so sluchainymi fazami, detektor budet registrirovat' gravitacionno-volnovoi shum,
uroven' kotorogo
, kotorye izluchayut
GV so sluchainymi fazami, detektor budet registrirovat' gravitacionno-volnovoi shum,
uroven' kotorogo
![]() . V sluchae dvoinyh sistem
uroven' fona GV
. V sluchae dvoinyh sistem
uroven' fona GV
![]() , gde
, gde ![]() - temp sliyaniya
etih sistem.
- temp sliyaniya
etih sistem.
Naibolee mnogochislenna populyaciya galakticheskih dvoinyh belyh karlikov (Bender 1990, Bender 1997, Postnov i Prohorov 1998), dvigayushihsya po krugovym orbitam. Uroven' stohasticheskogo fona GV ot etih sistem dostatochen, dlya togo, chtoby ego mozhno bylo zaregistrirovat' kosmicheskim interferometrom LISA. Obrazovanie i metody vychisleniya urovnya fona rassmotreny v rabotah Postnov i Prohorov 1998, Grishuk i dr. 2001.
V sluchae nekrugovyh orbit GV-svetimost' vyshe, nezheli v krugovom sluchae.
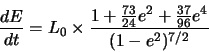
Krome togo, takie sistemy izluchayut ne na odnoi chastote (udvoennoi orbital'noi),
a v shirokom diapazone chastot.
gde
3.2.1 Obrazovanie stohasticheskogo fona ot dvoinyh sistem na ellipticheskih orbitah.
Rassmotrim nekotoryi interval chastot (v dal'neishem - bin)
![]() ,
takoi, chto
,
takoi, chto
![]() .
V etot bin popadaet izluchenie ot dvoinyh sistem, kotorye imeyut orbital'nuyu
chastotu
.
V etot bin popadaet izluchenie ot dvoinyh sistem, kotorye imeyut orbital'nuyu
chastotu
![]() i izluchayut na pervoi garmonike.
i izluchayut na pervoi garmonike.
Chislo takih sistem mozhno naiti iz stacionarnoi funkcii raspredeleniya
![]() . Takzhe v etot chastotnyi interval popadaet izluchenie
ot sistem s orbital'noi chastotoi
. Takzhe v etot chastotnyi interval popadaet izluchenie
ot sistem s orbital'noi chastotoi
![]() ,
kotorye izluchayut na vtoroi garmonike. I tak dalee.
Summarnaya energiya, izluchaemaya v edinicu vremeni na chastote
,
kotorye izluchayut na vtoroi garmonike. I tak dalee.
Summarnaya energiya, izluchaemaya v edinicu vremeni na chastote ![]() v
chastotnyi interval
v
chastotnyi interval ![]()
Stoit zametit', chto pri uvelichenii nomera garmoniki umen'shaetsya interval orbital'noi
chastoty sistemy
 , izluchenie ot kotoroi mozhet popast'
v nablyudaemyi chastotnyi bin.
, izluchenie ot kotoroi mozhet popast'
v nablyudaemyi chastotnyi bin.
Ostalos' tol'ko poyasnit', chto takoe ![]() . Amplituda vysokih garmonik
. Amplituda vysokih garmonik ![]() bystro umen'shaetsya (sm. risunok 3.1), i my ostanavlivaem
summirovanie po garmonikam pri
bystro umen'shaetsya (sm. risunok 3.1), i my ostanavlivaem
summirovanie po garmonikam pri ![]() , kotoroe opredelim sleduyushim obrazom.
, kotoroe opredelim sleduyushim obrazom.
![]() , takim obrazom vklad ot garmoniki
, takim obrazom vklad ot garmoniki ![]() budet
v
budet
v ![]() raz men'she vklada ot garmoniki
raz men'she vklada ot garmoniki ![]() . Pri raschetah ispol'zovalis' znacheniya
. Pri raschetah ispol'zovalis' znacheniya
![]() . Pri umen'shenii
. Pri umen'shenii ![]() uvelichivaetsya chislo garmonik,
popadayushih v chastotnyi bin, no prakticheski ne menyaetsya chislo naibolee moshnyh garmonik v bine.
uvelichivaetsya chislo garmonik,
popadayushih v chastotnyi bin, no prakticheski ne menyaetsya chislo naibolee moshnyh garmonik v bine.
3.2.2 Stacionarnyi stohasticheskii fon ot slivayushihsya NZ.
Rasschitaem GV-fon dlya prostoi modeli, v kotoroi vse dvoinye sistemy
obrazuyutsya v odnoi tochke fazovogo prostranstva ![]() s tempom rozhdeniya (i sliyaniya)
s tempom rozhdeniya (i sliyaniya)
![]() god
god![]() . Sledovatel'no, nachal'naya funkciya raspredeleniya imeet vid
del'ta-funkcii. Rasschitav stacionarnuyu funkciyu raspredeleniya mozhno postroit' spektr GV-fona,
izobrazhennogo na risunkah
3.3-3.4 dlya
. Sledovatel'no, nachal'naya funkciya raspredeleniya imeet vid
del'ta-funkcii. Rasschitav stacionarnuyu funkciyu raspredeleniya mozhno postroit' spektr GV-fona,
izobrazhennogo na risunkah
3.3-3.4 dlya
![]() i
i ![]() i
i ![]() sootvetstvenno.
sootvetstvenno.
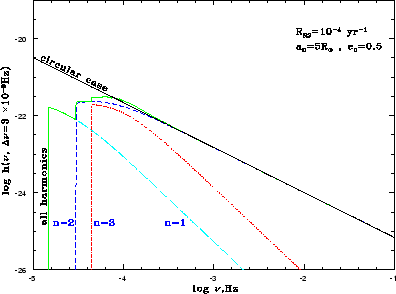 |
| Ris. 3.3
GV-fon i vklady v nego pervoi, vtoroi i tret'ei garmoniki. Vse sistemy
formiruyutsya s
|
Krome togo, na risunkah 3.3-3.4 izobrazheny vklady pervyh treh garmonik v obshii GV-fon. Vidno, chto uvelichenie nachal'nogo ekscentrisiteta sil'no vliyaet na vid spektra do nekotoroi chastoty, pri kotoroi ekscentrisitety dvoinyh, formiruyushih GV-fon, stanovyatsya neznachitel'nymi. Na chastotah vyshe etoi chastoty tol'ko izluchenie na vtoroi garmonike ot pochti krugovyh orbit opredelyaet obshii spektr. Nemonotonnaya zavisimost' obshego spektra i vkladov otdel'nyh garmonik ot chastoty yavlyaetsya sledstviem nemonotonnoi zavisimosti energii izluchaemoi na kazhdoi garmonike ot ekscentrisiteta.
Teper' rassmotrim stohasticheskii fon GV ot galakticheskih dvoinyh NZ na ellipticheskih
orbitah. Predpolagaem, chto vse istochniki nahodyatsya na odnom rasstoyanii,
a imenno ![]() kpk (sm. chast' 2.1).
kpk (sm. chast' 2.1).
Na kazhdoi chastote my summiruem GV-potok ot vseh garmonik popadayushih v chastotnyi
bin
![]() Gc ot dvoinyh sistem s poschitannoi stacionarnoi
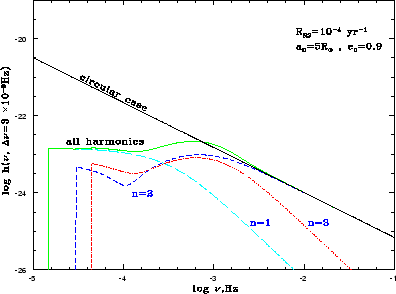
funkciei raspredeleniya (sm. (2.5)). Rezul'tiruyushii fon izobrazhen na risunke 3.5
v terminah bezrazmernoi amplitudy variacii metriki
Gc ot dvoinyh sistem s poschitannoi stacionarnoi
funkciei raspredeleniya (sm. (2.5)). Rezul'tiruyushii fon izobrazhen na risunke 3.5
v terminah bezrazmernoi amplitudy variacii metriki ![]() , kotoruyu my opredelyaem
sootnosheniem.
, kotoruyu my opredelyaem
sootnosheniem.
 |
| Ris. 3.5
GV-fon ot slivayushihsya dvoinyh neitronnyh zvezd v nashei Galaktike s tempom sliyaniya
|
Kak i ozhidalos', uroven' stohasticheskogo fona, obrazovannyi slivayushimisya dvoinymi
neitronnymi zvezdami, lezhit nizhe urovnya stohasticheskogo fona slivayushihsya belyh karlikov
glavnym obrazom iz-za malogo tempa sliyaniya ![]() .
Bol'shie garmoniki ot nekrugovyh sistem dayut osnovnoi vklad v obshii fon
na nizkih chastotah, nachinaya s chastoty
.
Bol'shie garmoniki ot nekrugovyh sistem dayut osnovnoi vklad v obshii fon
na nizkih chastotah, nachinaya s chastoty
![]() Gc vychislennyi fon prakticheski
ne otlichaetsya ot fona, kotoryi by formirovali dvoinye NZ na krugovyh orbitah
s takim zhe tempom sliyaniya
Gc vychislennyi fon prakticheski
ne otlichaetsya ot fona, kotoryi by formirovali dvoinye NZ na krugovyh orbitah
s takim zhe tempom sliyaniya
![]() god
god![]() .
.
Uroven' vnegalakticheskogo fona ot dvoinyh neitronnyh zvezd dazhe s uchetom sil'noi zavisimosti tempa zvezdoobrazovaniya ot krasnogo smesheniya i kosmologicheskih effektov ne mozhet sostavlyat' bolee chem 10% ot urovnya galakticheskogo fona (Kosenko i Postnov 1998, Shnaider 2001) i poetomu ego rassmatrivat' ne budem.
V predpolozhenii stacionarnosti uroven' fona na chastotah vyshe ![]() takzhe imeet fizicheskii smysl.
Deistvitel'no, pri bol'shom kolichestve (
takzhe imeet fizicheskii smysl.
Deistvitel'no, pri bol'shom kolichestve (
![]() ) nablyudenii dlitel'nost'yu
odin god kazhdoe, usrednennyi spektr po vsem etim nablyudeniyam
i sostavit stacionarnyi stohasticheskii fon GV.
Na risunke 3.5 izobrazhen dlinnymi shtrihami.
) nablyudenii dlitel'nost'yu
odin god kazhdoe, usrednennyi spektr po vsem etim nablyudeniyam
i sostavit stacionarnyi stohasticheskii fon GV.
Na risunke 3.5 izobrazhen dlinnymi shtrihami.
3.2.3 Predel'naya chastota
Krome urovnya fona est' eshe odna vazhnaya velichina, kotoraya harakterizuet stohasticheskii fon.
Eto predel'naya chastota ![]() , t.e. takaya chastota, vyshe kotoroi
individual'nye istochniki mozhno budet razreshit' za vremya nablyudenii
, t.e. takaya chastota, vyshe kotoroi
individual'nye istochniki mozhno budet razreshit' za vremya nablyudenii ![]() god.
Takim obrazom, predel'naya chastota opredelyaet granicu, pri nablyudeniyah na chastotah vyshe
kotoroi principial'no vozmozhno razreshit' individual'nye istochniki, a takzhe
detektirovat' bolee slabye
stohasticheskie fony (naprimer, reliktovye gravitacionnye volny, nesushie
informaciyu o rannih stadiyah razvitiya Vselennoi
god.
Takim obrazom, predel'naya chastota opredelyaet granicu, pri nablyudeniyah na chastotah vyshe
kotoroi principial'no vozmozhno razreshit' individual'nye istochniki, a takzhe
detektirovat' bolee slabye
stohasticheskie fony (naprimer, reliktovye gravitacionnye volny, nesushie
informaciyu o rannih stadiyah razvitiya Vselennoi
![]() sek, sm. Grishuk i dr. 2001).
sek, sm. Grishuk i dr. 2001).
Ocenku ![]() mozhno poluchit' iz sleduyushih soobrazhenii. Rassmotrim uzkii interval chastot
mozhno poluchit' iz sleduyushih soobrazhenii. Rassmotrim uzkii interval chastot
![]() . Chastota izlucheniya ot dvoinyh sistem, vsledstvie unosa GV energii
i uglovogo momenta, uvelichivaetsya, i izluchenie ot opredelennogo istochnika cherez
nekotoroe vremya perestanet popadat' v pervonachal'nyi chastotnyi bin.
. Chastota izlucheniya ot dvoinyh sistem, vsledstvie unosa GV energii
i uglovogo momenta, uvelichivaetsya, i izluchenie ot opredelennogo istochnika cherez
nekotoroe vremya perestanet popadat' v pervonachal'nyi chastotnyi bin.
Pust' s tempom ![]() - istochniki poyavlyayutsya v chastotnom okne, i nahodyatsya
tam vremya
- istochniki poyavlyayutsya v chastotnom okne, i nahodyatsya
tam vremya
![]() . Takim obrazom, chislo sistem v etom intervale chastot
. Takim obrazom, chislo sistem v etom intervale chastot
 .
Iz usloviya
.
Iz usloviya
![]() mozhno opredelit'
mozhno opredelit' ![]() .
.
Dlya galakticheskoi populyacii slivayushihsya BK, kotorye nahodyatsya na pochti krugovyh orbitah
(sm. Grishuk i dr. 2001)
My budem schitat' chislo takih garmonik, vklad kotoryh v GV - potok na dannoi chastote
sostavlyaet ![]() ot obshego potoka.
Chislo takih garmonik
ot obshego potoka.
Chislo takih garmonik
![]() kak funkciya chastoty
kak funkciya chastoty ![]() izobrazhena na risunke
3.6 dlya razlichnyh predpolagaemyh amplitud skorosti «otdachi» vo vremya
vspyshki sverhnovoi. Predel'naya chastota
izobrazhena na risunke
3.6 dlya razlichnyh predpolagaemyh amplitud skorosti «otdachi» vo vremya
vspyshki sverhnovoi. Predel'naya chastota ![]() opredelyaemaya iz uravneniya
opredelyaemaya iz uravneniya
![]() pri nashih neopredelennostyah
(
pri nashih neopredelennostyah
(![]() ,
, ![]() ,
, ![]() i dr.) prinimaet znachenie
i dr.) prinimaet znachenie
![]() Gc, chto poryadka analogichnoi velichine dlya slivayushihsya BK.
Dlya sravneniya na risunke 3.6 pokazano
Gc, chto poryadka analogichnoi velichine dlya slivayushihsya BK.
Dlya sravneniya na risunke 3.6 pokazano
![]() dlya sluchaya krugovyh
orbit dvoinyh neitronnyh zvezd.
dlya sluchaya krugovyh
orbit dvoinyh neitronnyh zvezd.
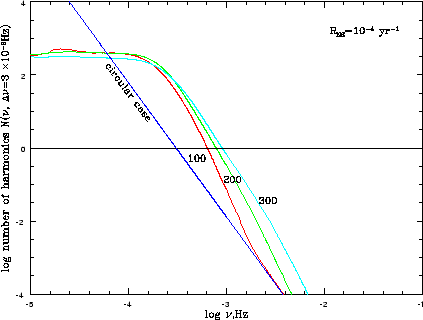 |
| Ris. 3.6
Chislo garmonik v intervale chastot |
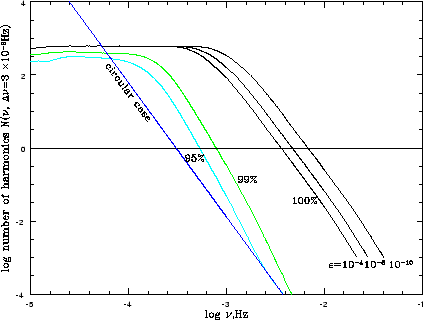 |
| Ris. 3.7
Chislo naibolee moshnyh garmonik v bine |
Effekt zavisimosti ot vybrannogo urovnya GV-potoka ot naibolee moshnyh garmonik
izobrazhen na risunke 3.7. Uvelichenie urovnya s ![]() do
do ![]() uvelichivaet
znachenie
uvelichivaet
znachenie ![]() pochti na poryadok.
pochti na poryadok.
Teper' rassmotrim chastotnye biny na chastote ![]() bol'she predel'noi chastoty
bol'she predel'noi chastoty ![]() .
Mozhno otvetit' na vopros, u kakih iz garmonik popadayushih vnutr'
bina naibol'shaya veroyatnost' nahodit'sya v bine, i u kakih ona naimen'shaya. Eta veroyatnost'
opredelyaetsya nomerom garmoniki i stacionarnoi funkciei raspredeleniya
.
Mozhno otvetit' na vopros, u kakih iz garmonik popadayushih vnutr'
bina naibol'shaya veroyatnost' nahodit'sya v bine, i u kakih ona naimen'shaya. Eta veroyatnost'
opredelyaetsya nomerom garmoniki i stacionarnoi funkciei raspredeleniya
![]() . Naimenee veroyatnye, eto garmoniki ot sistem
s maksimal'noi orbital'noi chastotoi
. Naimenee veroyatnye, eto garmoniki ot sistem
s maksimal'noi orbital'noi chastotoi ![]() , izluchenie ot kotoryh popadaet v chastotnyi
bin
, izluchenie ot kotoryh popadaet v chastotnyi
bin ![]() na pervoi garmonike. Provedem takuyu operaciyu: otbrosim
vklad ot sistem, izluchenie ot kotoryh na pervoi garmonike
popadaet vnutr' chastotnogo intervala
na pervoi garmonike. Provedem takuyu operaciyu: otbrosim
vklad ot sistem, izluchenie ot kotoryh na pervoi garmonike
popadaet vnutr' chastotnogo intervala
![]() pri
pri ![]() .
Pri etom teryaetsya nekotoraya chast' obshego GV-potoka i mozhno naiti novuyu ocenku
predel'noi chastoty
.
Pri etom teryaetsya nekotoraya chast' obshego GV-potoka i mozhno naiti novuyu ocenku
predel'noi chastoty ![]() . Dlya chastot
. Dlya chastot
![]() provedem
podobnuyu operaciyu. Zdes' naimenee veroyatnoi garmonikoi budet vtoraya. Nahodim sootvetstvuyushuyu
etomu sluchayu predel'nuyu chastotu
provedem
podobnuyu operaciyu. Zdes' naimenee veroyatnoi garmonikoi budet vtoraya. Nahodim sootvetstvuyushuyu
etomu sluchayu predel'nuyu chastotu ![]() . I tak dalee, otbrasyvaem vklady ot 3-ei,
4-oi,...,
. I tak dalee, otbrasyvaem vklady ot 3-ei,
4-oi,...,![]() -oi garmonik, poka uroven' ostavshegosya fona ne stanet men'she urovnya chuvstvitel'nosti
detektora.
-oi garmonik, poka uroven' ostavshegosya fona ne stanet men'she urovnya chuvstvitel'nosti
detektora.
Kak uzhe govorilos' vyshe, naimen'shaya veroyatnost' popadaniya garmoniki v bin u garmonik s malym ![]() ,
no vmeste s tem eti garmoniki vnosyat sushestvennyi vklad v obshii uroven' fona. Na bol'shih
chastotah pochti vse izluchenie popadayushee v chastotnyi bin opredelyaet vtoraya garmonika. Sootvetstvenno,
uroven' fona - imenno fona, tak kak otbroshennye garmoniki redkie i pri etom «moshnye» -
dlya togo chtoby ih mozhno bylo razreshit', budet rezko umen'shat'sya s chastotoi. Uroven'
stohasticheskogo fona ot dvoinyh neitronnyh zvezd,
posle provedeniya takoi operacii izobrazhen na risunke
3.5 lomanoi liniei, a predel'naya chastota
,
no vmeste s tem eti garmoniki vnosyat sushestvennyi vklad v obshii uroven' fona. Na bol'shih
chastotah pochti vse izluchenie popadayushee v chastotnyi bin opredelyaet vtoraya garmonika. Sootvetstvenno,
uroven' fona - imenno fona, tak kak otbroshennye garmoniki redkie i pri etom «moshnye» -
dlya togo chtoby ih mozhno bylo razreshit', budet rezko umen'shat'sya s chastotoi. Uroven'
stohasticheskogo fona ot dvoinyh neitronnyh zvezd,
posle provedeniya takoi operacii izobrazhen na risunke
3.5 lomanoi liniei, a predel'naya chastota ![]() okazyvaetsya poryadka
okazyvaetsya poryadka ![]() mGc.
Konechno, eta krivaya ne predstavlyaet soboi real'nogo
stohasticheskogo fona GV ot slivayushihsya galakticheskih dvoinyh NZ i daet predstavlenie tol'ko
o ego povedenii na chastotah bol'she predel'noi chastoty
mGc.
Konechno, eta krivaya ne predstavlyaet soboi real'nogo
stohasticheskogo fona GV ot slivayushihsya galakticheskih dvoinyh NZ i daet predstavlenie tol'ko
o ego povedenii na chastotah bol'she predel'noi chastoty
![]() mGc.
Na chastotah nizhe predel'noi uroven' stohasticheskogo fona opredelyaetsya
stacionarnym stohasticheskim fonom rasschitannym vyshe.
mGc.
Na chastotah nizhe predel'noi uroven' stohasticheskogo fona opredelyaetsya
stacionarnym stohasticheskim fonom rasschitannym vyshe.
3.3 Shirokopolosnyi GV-signal
GV-izluchenie ot dvoinyh zvezd nashei Galaktiki obrazuet stohasticheskii fon
na chastotah
![]() Gc i mozhet byt' obnaruzheno kosmicheskim interferometrom
LISA. Na chastotah vyshe predel'noi chastoty (sm. chast' 3.2.3)
Gc i mozhet byt' obnaruzheno kosmicheskim interferometrom
LISA. Na chastotah vyshe predel'noi chastoty (sm. chast' 3.2.3)
![]() Gc
mozhno budet registrirovat' gravitacionnye volny ot otdel'nyh sistem za vremya nablyudeniya odin god.
Obnaruzhit' GV ot dvoinoi sistemy na krugovoi orbite za god nablyudenii, skoree vsego ne udastsya,
tak kak slishkom mala veroyatnost' takogo sobytiya. Napomnim, chto temp sliyaniya dvoinyh neitronnyh
zvezd
Gc
mozhno budet registrirovat' gravitacionnye volny ot otdel'nyh sistem za vremya nablyudeniya odin god.
Obnaruzhit' GV ot dvoinoi sistemy na krugovoi orbite za god nablyudenii, skoree vsego ne udastsya,
tak kak slishkom mala veroyatnost' takogo sobytiya. Napomnim, chto temp sliyaniya dvoinyh neitronnyh
zvezd
![]() v god, a belyh karlikov
v god, a belyh karlikov
![]() let
let![]() .
V tozhe vremya veroyatnost' obnaruzhit' izluchenie ot dvoinyh sistem nashei Galaktiki
v chastotnom diapazone
.
V tozhe vremya veroyatnost' obnaruzhit' izluchenie ot dvoinyh sistem nashei Galaktiki
v chastotnom diapazone
![]() Gc ves'ma velika. Eto svyazano s dvoinymi sistemami
na sil'no vytyanutyh orbitah, izluchenie ot kotoryh proishodit na bol'shih garmonikah.
Chto zhe predstavlyaet iz sebya eto izluchenie? Maksimum izlucheniya GV ot dvoinyh zvezd
na ellipticheskih orbitah prihoditsya na momenty vblizi prohozhdeniya periastra
Gc ves'ma velika. Eto svyazano s dvoinymi sistemami
na sil'no vytyanutyh orbitah, izluchenie ot kotoryh proishodit na bol'shih garmonikah.
Chto zhe predstavlyaet iz sebya eto izluchenie? Maksimum izlucheniya GV ot dvoinyh zvezd
na ellipticheskih orbitah prihoditsya na momenty vblizi prohozhdeniya periastra ![]() .
GV-izluchenie ot takoi sistem budet nosit' harakter shirokopolosnyh impul'sov s periodom povtoreniya
(orbital'nym periodom) ot desyatkov minut do neskol'kih chasov v diapazone chastot
.
GV-izluchenie ot takoi sistem budet nosit' harakter shirokopolosnyh impul'sov s periodom povtoreniya
(orbital'nym periodom) ot desyatkov minut do neskol'kih chasov v diapazone chastot
![]() Gc.
Dlitel'nost' takogo impul'sa opredelyaetsya vremenem proleta vblizi periastra, gde proishodit
intensivnaya generaciya GV. Dlya bol'shih ekscentrisitetov dlitel'nost' impul'sa priblizhenno
ravna
Gc.
Dlitel'nost' takogo impul'sa opredelyaetsya vremenem proleta vblizi periastra, gde proishodit
intensivnaya generaciya GV. Dlya bol'shih ekscentrisitetov dlitel'nost' impul'sa priblizhenno
ravna ![]() (
(![]() - skorost' dvizheniya v periastre), i maksimum izlucheniya prihoditsya
na garmoniku
- skorost' dvizheniya v periastre), i maksimum izlucheniya prihoditsya
na garmoniku
![]() v sootvetstvii s tret'im zakonom Keplera.
v sootvetstvii s tret'im zakonom Keplera.
3.3.1 GV-signal ot dvoinyh sistem pri prohozhdenii periastra
Opredelim vremya izlucheniya osnovnoi chasti energii pri dvizhenii NZ vblizi periastra.
Dlya etogo vospol'zuemsya vyrazheniem dlya izlucheniya GV ot dvuh tochechnyh mass
na ellipticheskih orbitah, usrednennym po prostranstvennoi orientacii orbity
(Landau i Lifshic 1973)
Pereidem ot integrirovaniya po vremeni ![]() k integrirovaniyu po polyarnomu uglu
k integrirovaniyu po polyarnomu uglu
Zavisimost' ![]() i
i ![]() ot ekscentrisiteta izobrazhena na risunke 3.8.
Vidno, chto nachinaya s ekscentrisiteta
ot ekscentrisiteta izobrazhena na risunke 3.8.
Vidno, chto nachinaya s ekscentrisiteta ![]() ugol
ugol
![]() i slabo
menyaetsya pri dal'neishem uvelichenii ekscentrisiteta. Eto mozhet byt' ponyatno iz sleduyushih
soobrazhenii: periastral'noe rasstoyanie
i slabo
menyaetsya pri dal'neishem uvelichenii ekscentrisiteta. Eto mozhet byt' ponyatno iz sleduyushih
soobrazhenii: periastral'noe rasstoyanie ![]() i fokal'nyi parametr ellipsa orbity
i fokal'nyi parametr ellipsa orbity
![]() pri bol'shih ekscentrisitetah menyayutsya odinakovo
pri bol'shih ekscentrisitetah menyayutsya odinakovo ![]() i, sledovatel'no periastral'nye chasti orbit pri razlichnyh
i, sledovatel'no periastral'nye chasti orbit pri razlichnyh ![]() podobny drug drugu.
podobny drug drugu.
Takzhe iz risunka 3.8 sleduet, chto pri ekscentrisitete okolo ![]()
![]() energii
vysvechivaetsya za
energii
vysvechivaetsya za ![]() orbital'nogo perioda. V dal'neishem my budem brat' znachenie
orbital'nogo perioda. V dal'neishem my budem brat' znachenie ![]() v kachestve nizhnei granicy ekscentrisitetov dvoinyh zvezd, dayushih shirokopolosnye impul'sy GV.
v kachestve nizhnei granicy ekscentrisitetov dvoinyh zvezd, dayushih shirokopolosnye impul'sy GV.
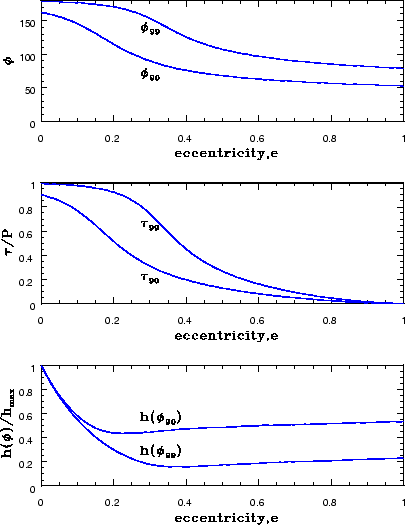 |
| Ris. 3.8
Verhnyaya panel': polyarnyi ugol |
Takim obrazom, pri prohozhdenii periastra dvoinaya NZ na ellipticheskoi orbite budet izluchat'
signal v shirokom intervale chastot
![]() . Takie impul'sy
harakterizuyutsya dlitel'nost'yu
. Takie impul'sy
harakterizuyutsya dlitel'nost'yu ![]() , periodom povtoreniya
, periodom povtoreniya ![]() i amplitudoi,
v kachestve ocenki kotoroi voz'mem maksimal'nuyu bezrazmernuyu amplitudu
i amplitudoi,
v kachestve ocenki kotoroi voz'mem maksimal'nuyu bezrazmernuyu amplitudu ![]() gravitacionnoi
volny v periastre. Usrednyaya kvadraty amplitud GV-polya razlichnyh polyarizacii po prostranstvennoi
orientacii sistemy, poluchaem
gravitacionnoi
volny v periastre. Usrednyaya kvadraty amplitud GV-polya razlichnyh polyarizacii po prostranstvennoi
orientacii sistemy, poluchaem
3.3.2 Osobennosti detektirovaniya shirokopolosnyh GV-signalov
Teper', esli my hotim rascchitat' ozhidaemyi temp detektirovaniya GV-impul'sov ot dvoinyh sistem na ellipticheskih orbitah, sleduet tochnee opredelit', chto my budem nazyvat' impul'som i zapisat' dlya takogo signala otnoshenie signal k shumu.
Dvoinye NZ na vytyanutoi orbite, izluchenie ot kotoryh v periastre popadaet
v chastotnyi diapazon
![]() Gc, mogut imet' orbital'nye periody
ot desyatkov minut do neskol'kih chasov (sm. risunok 3.9).
Gc, mogut imet' orbital'nye periody
ot desyatkov minut do neskol'kih chasov (sm. risunok 3.9).
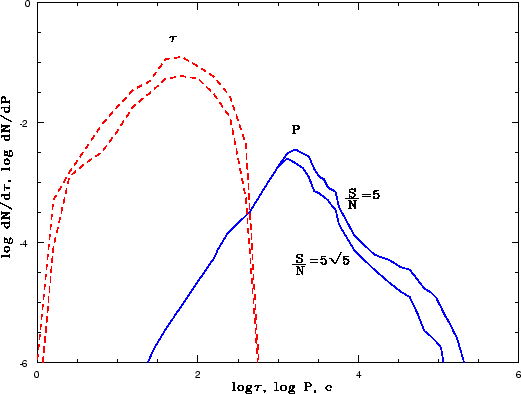 |
| Ris. 3.9
Raspredelenie dvoinyh NZ, ot kotoryh signal v periastre prevoshodit uroven' fona
v |
Predpolagaem, chto izmenenie energii i momenta impul'sa sistemy za odin orbital'nyi
period malo i parametry orbity ne menyayutsya. Eto dopushenie vypolnyaetsya dlya rassmatrivaemyh
chastot. Togda za vremya nablyudeniya ![]() god signal ot odnoi sistemy budet predstavlyat'
periodicheskuyu posledovatel'nost', sostoyashuyu iz
god signal ot odnoi sistemy budet predstavlyat'
periodicheskuyu posledovatel'nost', sostoyashuyu iz ![]() shirokopolosnyh impul'sov so
sluchainoi fazoi otnositel'no nachala nablyudenii. Takzhe neizvestna prostranstvennaya orientaciya
sistemy, napravlenie i rasstoyanie do nee. Sledovatel'no, signal na detektore budet
predstavlyat' iz sebya summu periodicheskih posledovatel'nostei impul'sov
shirokopolosnyh impul'sov so
sluchainoi fazoi otnositel'no nachala nablyudenii. Takzhe neizvestna prostranstvennaya orientaciya
sistemy, napravlenie i rasstoyanie do nee. Sledovatel'no, signal na detektore budet
predstavlyat' iz sebya summu periodicheskih posledovatel'nostei impul'sov ![]() so sluchainymi
fazami, razlichnymi amplitudami i periodami povtorenii
so sluchainymi
fazami, razlichnymi amplitudami i periodami povtorenii
![]() .
Vazhno zametit', chto v rassmatrivaemom diapazone chastot takoi signal ne obrazuet stohasticheskogo
fona (sm. chast' 3.2) pri chastotnom razreshenii detektora
.
Vazhno zametit', chto v rassmatrivaemom diapazone chastot takoi signal ne obrazuet stohasticheskogo
fona (sm. chast' 3.2) pri chastotnom razreshenii detektora
![]() Gc.
Gc.
Snachala rassmotrim chastnyi sluchai, kogda v rassmatrivaemom intervale chastot imeetsya tol'ko
odna posledovatel'nost' impul'sov. Otnoshenie signala k shumu pri nablyudenii
impul'sa s dlitel'nost'yu ![]() detektorom s chuvstvitel'nost'yu
detektorom s chuvstvitel'nost'yu ![]() (imeet razmernost'
(imeet razmernost'
![]() , sm. tochnoe opredelenie i obsuzhdenie v obzore Grishuk i dr. 2001).
, sm. tochnoe opredelenie i obsuzhdenie v obzore Grishuk i dr. 2001).
Dlya periodicheskoi posledovatel'nosti sostoyashei iz ![]() odinakovyh impul'sov otnoshenie signala k
shumu uvelichitsya
odinakovyh impul'sov otnoshenie signala k
shumu uvelichitsya
V kachestve real'nogo primera rassmotrim Hals-Teilorovskii pul'sar PSR B1913+16 i naidem dlya nego
otnoshenie signala k shumu. Orbital'nye parametry etoi dvoinoi sistemy sostoyashei iz
dvuh NZ (Teilor, Vaisberg 1989): bol'shaya poluos'
![]() sm, orbital'nyi period
sm, orbital'nyi period
![]() s, ekscentrisitet
s, ekscentrisitet ![]() . Massy obeih komponent s bol'shoi tochnost'yu sovpadayut
. Massy obeih komponent s bol'shoi tochnost'yu sovpadayut
![]() , rasstoyanie do sistemy
, rasstoyanie do sistemy ![]() kpk. Usrednyaya po prostranstvennoi
orientacii (budem schitat' ee neizvestnoi) nahodim
kpk. Usrednyaya po prostranstvennoi
orientacii (budem schitat' ee neizvestnoi) nahodim
![]() . Dlya ekscentrisiteta
0.617 dlitel'nost' impul'sa
. Dlya ekscentrisiteta
0.617 dlitel'nost' impul'sa
![]() c, shirina impul'sa v chastotnom predstavlenii
c, shirina impul'sa v chastotnom predstavlenii
![]() mGc, chastota maksimal'noi (4-oi) garmoniki
mGc, chastota maksimal'noi (4-oi) garmoniki ![]() mGc.
Otnoshenie signala k shumu za god nepreryvnyh nablyudenii, ocenennoe po formule (3.20)
ravno 0.5 (bez ucheta shuma ot galakticheskih belyh karlikov, GV-fon kotoryh opredelyaet
astrofizicheskii shum na detektore v dannom intervale chastot). Vidno, chto PSR B1913+16
nevozmozhno budet zaregistrirovat', i takie istochniki nam ne interesny.
mGc.
Otnoshenie signala k shumu za god nepreryvnyh nablyudenii, ocenennoe po formule (3.20)
ravno 0.5 (bez ucheta shuma ot galakticheskih belyh karlikov, GV-fon kotoryh opredelyaet
astrofizicheskii shum na detektore v dannom intervale chastot). Vidno, chto PSR B1913+16
nevozmozhno budet zaregistrirovat', i takie istochniki nam ne interesny.
Teper' rassmotrim galakticheskuyu populyaciyu dvoinyh neitronnyh zvezd. Vospol'zovavshis' rezul'tatami Glavy 2, postroim nachal'nuyu i stacionarnuyu funkcii raspredeleniya po orbital'nymi parametram. Krome togo, na stacionarnuyu funkciyu raspredeleniya nalozhim dopolnitel'nye usloviya, opredelyayushie ee granicy na fazovoi ploskosti.
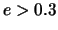 nizhnyaya granica ekscentrisitetov dvoinyh zvezd, GV-izluchenie ot kotoryh
predstavlyaetsya v vide impul'sov.
nizhnyaya granica ekscentrisitetov dvoinyh zvezd, GV-izluchenie ot kotoryh
predstavlyaetsya v vide impul'sov.
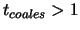 goda. Eto uslovie sleduet iz trebovaniya postoyanstva parametrov
orbity.
goda. Eto uslovie sleduet iz trebovaniya postoyanstva parametrov
orbity.
-
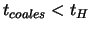 sleduet iz usloviya stacionarnosti.
sleduet iz usloviya stacionarnosti.
Vydelim na fazovoi ploskosti ![]() oblast', v kotoroi nahodyatsya sistemy
izluchayushie GV s amplitudoi, dayushei otnoshenie signal k shumu
oblast', v kotoroi nahodyatsya sistemy
izluchayushie GV s amplitudoi, dayushei otnoshenie signal k shumu ![]() (po prezhnemu schitaem, chto vse istochniki nahodyatsya na odinakovom rasstoyanii
(po prezhnemu schitaem, chto vse istochniki nahodyatsya na odinakovom rasstoyanii ![]() kpk).
Integriruya stacionarnuyu funkciyu raspredeleniya po etoi oblasti, poluchaem chislo takih sistem
kpk).
Integriruya stacionarnuyu funkciyu raspredeleniya po etoi oblasti, poluchaem chislo takih sistem
![]() . Ponizhenie poroga obnaruzheniya uvelichit chislo takih
sistem do 15, v sluchae
. Ponizhenie poroga obnaruzheniya uvelichit chislo takih
sistem do 15, v sluchae ![]() .
.
Poskol'ku na chastotah
![]() Gc imenno stohasticheskii fon
ot nerazreshennyh dvoinyh belyh karlikov opredelyaet uroven' shuma
na detektore (uroven' fona ot drugih populyacii kompaktnyh dvoinyh zvezd sushestvenno nizhe),
my takzhe uchityvali v kachestve shuma i etot fon.
3.1
Gc imenno stohasticheskii fon
ot nerazreshennyh dvoinyh belyh karlikov opredelyaet uroven' shuma
na detektore (uroven' fona ot drugih populyacii kompaktnyh dvoinyh zvezd sushestvenno nizhe),
my takzhe uchityvali v kachestve shuma i etot fon.
3.1
Raspredelenie sistem po dlitel'nosti impul'sov i
orbital'nym periodam privedeno na risunke 3.9. Vidno, chto naibolee veroyatno
obnaruzhit' impul'sy s dlitel'nost'yu okolo 100 sekund ot sistem s orbital'nym periodom
![]() cekund. Srednii ekscentrisitet pri etom
cekund. Srednii ekscentrisitet pri etom ![]() .
.
Takim obrazom, dlya stacionarnogo raspredeleniya dvoinyh NZ v Galaktike, sushestvuyut neskol'ko sistem s bol'shimi ekscentrisitetami i orbital'nymi periodami v diapazone ot neskol'kih desyatkov minut do neskol'kih chasov s dostatochno vysokoi amplitudoi GV v maksimume.
Sistemy massivnyi BK+NZ obladayut v srednem znachitel'no men'shim ekscentrisitetom
(srednii nachal'nyi ekscentrisitet takih sistem
![]() ), poetomu
dobavlennaya nizhnyaya granica po ekscentrisitetu
), poetomu
dobavlennaya nizhnyaya granica po ekscentrisitetu ![]() okazyvaetsya ves'ma kritichnoi
dlya opredeleniya chisla sistem, izluchenie ot kotoryh v periastre v vide shirokopolosnyh
impul'sov vozmozhno budet registrirovat' s bol'shim otnosheniem signala k shumu.
V sluchae stacionarnogo raspredeleniya, polnogo tempa sliyaniya
okazyvaetsya ves'ma kritichnoi
dlya opredeleniya chisla sistem, izluchenie ot kotoryh v periastre v vide shirokopolosnyh
impul'sov vozmozhno budet registrirovat' s bol'shim otnosheniem signala k shumu.
V sluchae stacionarnogo raspredeleniya, polnogo tempa sliyaniya
![]() god
god![]() i dlya otnosheniya signala k shumu
i dlya otnosheniya signala k shumu ![]() chislo sistem
chislo sistem ![]() , a pri
, a pri ![]() uvelichivaetsya do
uvelichivaetsya do ![]() . Vidno, chto obnaruzhit' takoi signal za god nablyudenii maloveroyatno.
Naibolee veroyatnaya dlitel'nost' impul'sa poryadka 300 sekund, a naibolee veroyatnyi
orbital'nyi period okolo 1000 sekund, kak i dlya dvoinyh neitronnyh zvezd.
Stoit zametit', chto shirokopolosnye GV-impul'sy ot dvoinyh NZ i sistem BK+NZ pochti
ni chem ne otlichayutsya, za isklyucheniem ih dlitel'nosti.
. Vidno, chto obnaruzhit' takoi signal za god nablyudenii maloveroyatno.
Naibolee veroyatnaya dlitel'nost' impul'sa poryadka 300 sekund, a naibolee veroyatnyi
orbital'nyi period okolo 1000 sekund, kak i dlya dvoinyh neitronnyh zvezd.
Stoit zametit', chto shirokopolosnye GV-impul'sy ot dvoinyh NZ i sistem BK+NZ pochti
ni chem ne otlichayutsya, za isklyucheniem ih dlitel'nosti.
<< 2. Stacionarnaya funkciya raspredeleniya | Oglavlenie | 4. Obsuzhdenie >>
|
Publikacii s klyuchevymi slovami:
dvoinye zvezdy - gravitacionnoe izluchenie
Publikacii so slovami: dvoinye zvezdy - gravitacionnoe izluchenie | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |