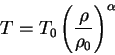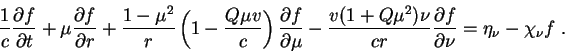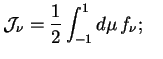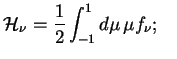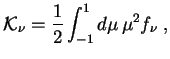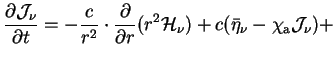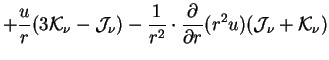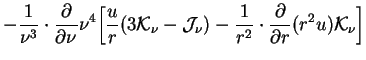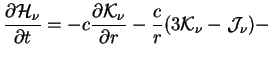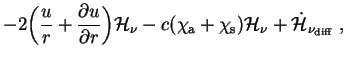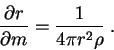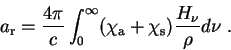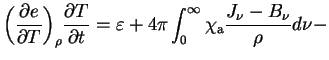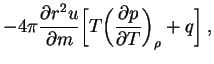Teoreticheskii katalog sverhnovyh vtorogo tipa
<< Vvedenie. Teoreticheskii katalog | Oglavlenie | 2. Rezul'taty modelirovaniya >>
1. Modelirovanie vzryva.
Sverhnovaya rassmatrivaetsya kak vzryv nekotorogo ravnovesnogo gazovogo
shara, dlya kotorogo stroitsya konfiguraciya(nazyvaemaya v dal'neishem predsverhnovaya)
s zaranee predpisannym raspredeleniem
himicheskogo sostava s zadannoi massoi i radiusom v gidrostaticheskom
ravnovesii. V rezul'tate poluchaem raspredelenie davleniya,
temperatury i plotnosti po radiusu. Zatem vnosim (nemaloe!)
nachal'noe vozmushenie v central'nyh zonah etogo shara, vydelyaem
teplovuyu ili kineticheskuyu energiyu poryadka nablyudaemoi kineticheskoi
energii vzryva sverhnovoi. Konechno, nachal'naya energiya dolzhna byt'
neskol'ko vyshe, tak kak zametnaya chast' uhodit na preodolenie
samogravitacii, a kakoi-to procent uhodit v izluchenie fotonov (tem
bol'shii, chem bol'she nachal'nyi radius, tak kak chem nizhe plotnost',
tem bol'she dolya entropii porozhdennoi udarnoi volnoi perehodit k
fotonnomu gazu).
1.1 Predsverhnovaya.
Chto znachit sozdanie predsverhnovoi?
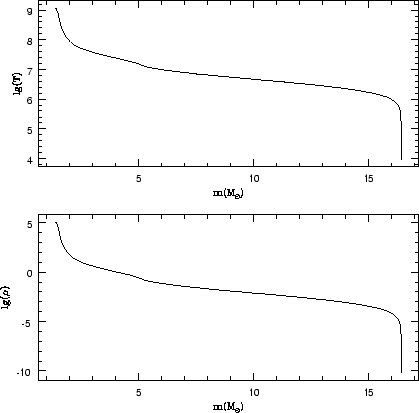
Sozdanie predsverhnovoi -- eto raschet ravnovesnogo gazovogo shara, podelennogo na 100 sfericheski-simmetrichnyh zon, v predelah kotoryh schitalos' deistvuet priblizhenie LTR. Dlya gazovogo shara zadavali global'nye parametry, kak massa, radius, him. sostav. Raspredelenie elementov po zvezde blizko k rezul'tatam evolyucionnogo modelirovaniya i privedeno na ris.(1.1)
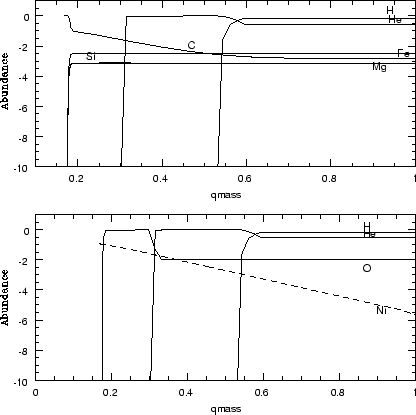 |
Ispol'zovalis' eshe menee znachitel'nye parametry, naprimer, plotnost' na granice zvezdy i dr., kotorye pri modelirovanii ne menyalis'.
Iz resheniya uravneniya gidrostaticheskogo ravnovesiya
vyvodilis' zavisimosti mezhdu
![]() .
.
Mezhdu temperaturai i plotnost'yu prinimalos' politropnoe sootnoshenie:
Zatem chislenno rasschityvalis' znacheniya T, ![]() , P v kazhdoi zone v
priblizhenii ideal'nogo gaza, no s polnym uchetom ionizacii po Saha.
Zavisimost' mezhdu
, P v kazhdoi zone v
priblizhenii ideal'nogo gaza, no s polnym uchetom ionizacii po Saha.
Zavisimost' mezhdu ![]() i
i ![]() pokazana na
ris. 1.2.
pokazana na
ris. 1.2.
Model' predsverhnovoi mozhno predstavit', kak tablicu:
po vertikali zadayutsya sloi(zony) v predsverhnovoi
po gorizontali -- parametry predsverhnovoi v etoi zone( T, ![]() , P i dr.)
, P i dr.)
Nizhe dan primer: pervye shest' strok iz tablicy dlya predsverhnovoi r500m3ni2 s
![]() ,
,
![]()
| zone | mass | ... | |||
| 1 | 1.414 | 8.853 | 9.030 | 4.894 | ... |
| 2 | 1.419 | 8.866 | 9.017 | 4.856 | ... |
| 3 | 1.426 | 8.883 | 9.001 | 4.807 | ... |
| 4 | 1.434 | 8.905 | 8.979 | 4.743 | ... |
| 5 | 1.446 | 8.934 | 8.951 | 4.658 | ... |
| 6 | 1.460 | 8.973 | 8.913 | 4.543 | ... |
| ... | ... | ... | ... | ... | ... |
1.2 Raschet neprozrachnosti.
Sleduyushim shagom, priblizhayushim nas sobstvenno k samomu vzryvu, byl
raschet neprozrachnosti. Dostatochno dlitel'nyi i utomitel'ni dlya
EVM process. V kazhdoi iz sta zon dlya kazhdogo iz sta intervalov
chastot schitalas' polnaya neprozrachnost' veshestva.
V polnuyu neprozrachnost' byli vklyucheny effekty fotoionizacii, svobodno-svobodnogo
poglosheniya, linii i elektronnoe rasseyanie. Uchteno bylo
![]() linii
v diapazone
ot
linii
v diapazone
ot ![]() do
do ![]() po dannym Kurucz R.L. 1991.
Ischerpyvayushuyu informaciyu po raschetu neprozrachnosti v pakete STELLA sm.([1]).
po dannym Kurucz R.L. 1991.
Ischerpyvayushuyu informaciyu po raschetu neprozrachnosti v pakete STELLA sm.([1]).
Pri raschete neprozrachnosti schitalos':
1) pri vzryve veshestvo ne peretekaet iz zony v zonu,
2) him. sostav v kazhdoi zone pri izmenenii radiusa predsverhnovoi
postoyanen,
3) neprozrachnost' ne zavisit ot energii vzryva.
Pri takih predpolozheniyah mozhno raschitat' tol'ko
chetyre tablicy neprozrachnosti: dlya kazhdoi massy(5.77, 8.41, 16.41, 20.41 ![]() ).
I ispol'zovat' ih pri raschete vspyshki dlya sootvetstvuyushei massy.
Takoi podhod dal vozmozhnost' rasschitat' bol'shee chislo modelei.
).
I ispol'zovat' ih pri raschete vspyshki dlya sootvetstvuyushei massy.
Takoi podhod dal vozmozhnost' rasschitat' bol'shee chislo modelei.
1.3 Raschet vzryva sverhnovoi.
Poluchiv tablicy neprozrachnosti i model' predsverhnovoi, stalo vozmozhnym, pristupat' k vzryvu zvezdy. Raschet vzryva sverhnovoi v programme STELLA provodilsya po sleduyushei sheme (sm. takzhe [1]).
Zapishem uravnenie Bol'cmana v soputstvuyushei sisteme otscheta dlya galileevskogo priblizheniya
(effekty ![]() ne uchityvayutsya) v sfericheski-simmetrichnom sluchae :
ne uchityvayutsya) v sfericheski-simmetrichnom sluchae :
I vvedem uglovye momenty funkcii raspredeleniya ![]() :
:
To sleduya [1], poluchim uravneniya v soputstvuyushei sisteme, v tom vide kak oni ispol'zuyutsya v programme (chastnaya proizvodnaya po vremeni beretsya pri fiksirovannoi lagranzhevoi koordinate). Posle integrirovaniya (1.2) po
Integrirovanie (1.2) po
plyus eshe neskol'ko chlenov, kotorymi mozhno prenebrech' Zdes'
Uravneniya (1.4) i (1.5) dlya vseh chastot (to est' dlya vseh chastotnyh grupp) reshayutsya odnovremenno s uravneniyami gidrodinamiki v lagranzhevyh koordinatah:
Zdes'
Neobhodimoe uravnenie dlya temperatury veshestva ![]() , mozhno
poluchit' iz pervogo nachala termodinamiki s pomosh'yu
(1.6), (1.8) i termodinamicheskogo tozhdestva:
, mozhno
poluchit' iz pervogo nachala termodinamiki s pomosh'yu
(1.6), (1.8) i termodinamicheskogo tozhdestva:
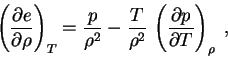 |
(1.10) |
Zdes'
Ponyatno, chto dlya zamykaniya sistemy
nado izbavit'sya ot
momenta ![]() . Prinimaetsya, chto
. Prinimaetsya, chto
V kachestve granichnyh uslovii
polagaetsya, chto na vneshnei granice (![]() , gde
, gde ![]() - polnaya
massa zvezdy) davlenie veshestva prenebrezhimo malo:
- polnaya
massa zvezdy) davlenie veshestva prenebrezhimo malo:
Vse proizvodnye po prostranstvu i chastote v
uravneniyah zamenyayutsya na konechnye raznosti. Pri etom neobhodimo proyavlyat'
akkuratnost' i ostorozhnost' pri usrednenii velichin s bol'shimi skachkami
mezhdu sosednimi zonami, pri perehode ot opticheski tonkih k opticheski
tolstym zonam, pri sshivke zon s polnym raschetom perenosa s zonami, gde
izluchenie opisyvaetsya v priblizhenii diffuzii ravnovesnogo izlucheniya.
Dlya kazhdoi iskomoi velichiny v kazhdoi raschetnoi yacheike
mozhno teper' traktovat' chastnye proizvodnye po vremeni kak polnye.
Takim obrazom, poluchaetsya sistema
obyknovennyh differencial'nyh uravnenii (ODU) dlya evolyucii ![]() ,
, ![]() ,
, ![]() v kazhdoi lagranzhevoi zone, a dlya
v kazhdoi lagranzhevoi zone, a dlya ![]() i
i ![]() eshe i
v kazhdoi gruppe po chastote.
Eto horosho izvestnyi metod linii, ili pryamyh,
kotoryi v dannom sluchae daet do
eshe i
v kazhdoi gruppe po chastote.
Eto horosho izvestnyi metod linii, ili pryamyh,
kotoryi v dannom sluchae daet do
![]() ODU, t.e.
do neskol'kih desyatkov tysyach uravnenii.
Dlya integrirovaniya etoi ogromnoi
sistemy ispol'zuetsya neyavnyi metod prognoza i korrekcii vysokogo poryadka po vremeni, osnovannyi na metodah Gira i
Braitona i dr. , s avtomaticheskim vyborom poryadka i
shaga po vremeni.
ODU, t.e.
do neskol'kih desyatkov tysyach uravnenii.
Dlya integrirovaniya etoi ogromnoi
sistemy ispol'zuetsya neyavnyi metod prognoza i korrekcii vysokogo poryadka po vremeni, osnovannyi na metodah Gira i
Braitona i dr. , s avtomaticheskim vyborom poryadka i
shaga po vremeni.
<< Vvedenie. Teoreticheskii katalog | Oglavlenie | 2. Rezul'taty modelirovaniya >>
|
Publikacii s klyuchevymi slovami:
Sverhnovye - krivaya bleska
Publikacii so slovami: Sverhnovye - krivaya bleska | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |