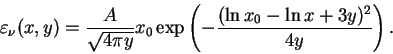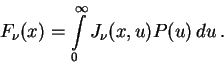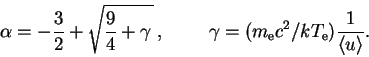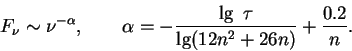<< 4. Kratkie harakteristiki istochnikov | Oglavlenie | 6. Vliyanie mezhzvezdnogo poglosheniya ... >>
5. Formirovanie rentgenovskih spektrov v processe komptonovskogo rasseyaniya.
Process obmena energiei mezhdu nerelyativistskimi fotonami (
![]() ) i nerelyativistskimi teplovymi elektronami (
) i nerelyativistskimi teplovymi elektronami (
![]() ) opisyvaetsya uravneniem
Kompaneica (1956):
) opisyvaetsya uravneniem
Kompaneica (1956):
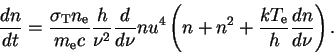 |
(15) |
| (16) |
| (17) |
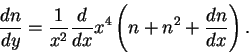 |
(18) |
- 1). Komptonovskoe rasseyanie sohranyaet chislo fotonov. Deistvitel'no,
- 2). Resheniem stacionarnogo uravneniya Kompaneica (
- 3). Uravnenie energeticheskogo balansa.
| (19) |
| (20) |
| (21) |
Srednyaya energiya fotona v raspredelenii Vina ravna:
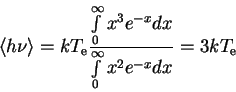 |
(22) |
Zadacha 2. Pryamym vychisleniem ubedit'sya, chto raspredelenie B-E
yavlyaetsya resheniem stacionarnogo uravneniya Kompaneica, a raspredelenie Vina -
resheniem stacionarnogo uravneniya Kompaneica bez ucheta inducirovannyh procesov,
t.e. bez chlena ![]() .
.
Umnozhim uravnenie Kompaneica na
![]() i prointegriruem ego po
chastote. Integrirovanie, proizvedennoe po chastyam v predelah ot nulya do
beskonechnosti daet (Levich i Syunyaev, 1971):
i prointegriruem ego po
chastote. Integrirovanie, proizvedennoe po chastyam v predelah ot nulya do
beskonechnosti daet (Levich i Syunyaev, 1971):
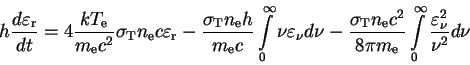 |
(23) |
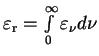 - integral'naya
plotnost' energii izlucheniya. Tak kak pri komptonovskom rasseyanii izmenenie
plotnosti energii izlucheniya ravno izmeneniyu vnutrennei energii elektronov, to
- integral'naya
plotnost' energii izlucheniya. Tak kak pri komptonovskom rasseyanii izmenenie
plotnosti energii izlucheniya ravno izmeneniyu vnutrennei energii elektronov, to
| (24) |
V stacionarnom sluchae
![]() , i mozhno naiti temperaturu
elektronov v pole izlucheniya s zadannym spektrom
(Zel'dovich i Levich, 1970):
, i mozhno naiti temperaturu
elektronov v pole izlucheniya s zadannym spektrom
(Zel'dovich i Levich, 1970):
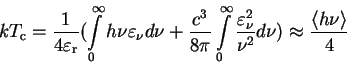 |
(25) |
Zadacha 3. Vyvesti uravnenie energeticheskogo balansa.
V tom sluchae, kogda fotony nizkih energii vzaimodeistvuyut s goryachimi
elektronami, mozhno prenebrech' pervymi dvumya chlenami v uravnenii Kompaneica, i
ono budet uchityvat' lish' doplerovskoe izmenenie chastoty pri rasseyanii.
Zel'dovich i Syunyaev (1969)
nashli reshenie poluchivshegosya diffuzionnogo uravneniya,
kotoroe v sluchae beskonechno uzkoi linii imeet vid:
Otmetim, chto formulirovka uravneniya Kompaneica kak izmenenie spektra fotonov
ot vremeni yavlyaetsya ochen' udobnoi pri rassmotrenii kosmologicheskih zadach.
Odnako pri rassmotrenii formirovaniya rentgenovskih spektrov v stacionarnyh
astrofizicheskih ob'ektah, takih kak akkrecionnye diski, neobhodimo pereiti
ot vremeni k prostranstvennoi peremennoi. Eto dostatochno prosto sdelat',
tak kak vvedennoe ranee bezrazmernoe vremya yavlyaetsya po smyslu takzhe elektronnoi
opticheskoi tolshoi ![]() , umnozhennoi na
, umnozhennoi na
![]() .
Takim obrazom, chem bol'shuyu opticheskuyu tolshu prohodyat fotony, tem bol'shee
vremya oni podvergayutsya vzaimodeistviyu s elektronami. V real'nosti kartina
neskol'ko slozhnee, i vremya vzaimodeistviya mezhdu fotonom i elektronami
opredelyaetsya chislom rasseyanii
.
Takim obrazom, chem bol'shuyu opticheskuyu tolshu prohodyat fotony, tem bol'shee
vremya oni podvergayutsya vzaimodeistviyu s elektronami. V real'nosti kartina
neskol'ko slozhnee, i vremya vzaimodeistviya mezhdu fotonom i elektronami
opredelyaetsya chislom rasseyanii ![]() , ispytannyh fotonom
, ispytannyh fotonom
![]() . Ishodya iz svoistv uravneniya Kompaneica, mozhno skazat',
chto pri bol'shom kolichestve rasseyanii, kogda
. Ishodya iz svoistv uravneniya Kompaneica, mozhno skazat',
chto pri bol'shom kolichestve rasseyanii, kogda ![]() iz sredy vyhodit
izluchenie, imeyushee spektral'noe raspredelenie Boze-Einshteina. Odnako pri
ne ochen' bol'shoi opticheskoi tolshe goryachih elektronov
iz sredy vyhodit
izluchenie, imeyushee spektral'noe raspredelenie Boze-Einshteina. Odnako pri
ne ochen' bol'shoi opticheskoi tolshe goryachih elektronov ![]() imeyutsya usloviya dlya formirovaniya stepennogo spektra. Takaya zadacha byla
reshena Syunyaevym i Titarchukom (1980).
imeyutsya usloviya dlya formirovaniya stepennogo spektra. Takaya zadacha byla
reshena Syunyaevym i Titarchukom (1980).
Rassmotrim ploskoparalel'nyi sloi goryachih elektronov opticheskoi tolshiny
![]() , cherez kotoryi prohodit izluchenie nizkoi chastoty so srednei energiei
, cherez kotoryi prohodit izluchenie nizkoi chastoty so srednei energiei
![]() . Srednee kolichestvo rasseyanii, ispytyvaemyh fotonami
pri prohozhdenii cherez sloi, ravno
. Srednee kolichestvo rasseyanii, ispytyvaemyh fotonami
pri prohozhdenii cherez sloi, ravno
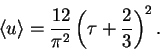 |
(27) |
Zdes'
gde
Zdes' postoyannye
Takim obrazom, my vidim, chto v spektral'noi oblasti
![]() formiruetsya stepenoi spektr. Vpolne ochevidno, chto pri bol'shih
chastotah, kogda nachinaet igrat' rol' effekt otdachi, formiruetsya Vinovskoe
raspredelenie s eksponencial'nym zavalom na vysokih chastotah.
Iz formuly (30)
vidno, chto naklon spektra (znachenie
formiruetsya stepenoi spektr. Vpolne ochevidno, chto pri bol'shih
chastotah, kogda nachinaet igrat' rol' effekt otdachi, formiruetsya Vinovskoe
raspredelenie s eksponencial'nym zavalom na vysokih chastotah.
Iz formuly (30)
vidno, chto naklon spektra (znachenie ![]() ) zavisit ot proizvedeniya
) zavisit ot proizvedeniya
![]() , t.e. ot opticheskoi tolshiny plazmy i ee elektronnoi temperatury.
Ispol'zuya etot fakt, mozhno po naklonu spektra rentgenovskogo istochnika
popytat'sya ocenit' eto znachenie. Bolee togo, esli v spektre imeetsya
eksponencial'nyi zaval, to po energii, gde nachinaetsya etot zaval
(
, t.e. ot opticheskoi tolshiny plazmy i ee elektronnoi temperatury.
Ispol'zuya etot fakt, mozhno po naklonu spektra rentgenovskogo istochnika
popytat'sya ocenit' eto znachenie. Bolee togo, esli v spektre imeetsya
eksponencial'nyi zaval, to po energii, gde nachinaetsya etot zaval
(![]() ), mozhno ocenit' znachenie temperatury, i ispol'zuya ee,
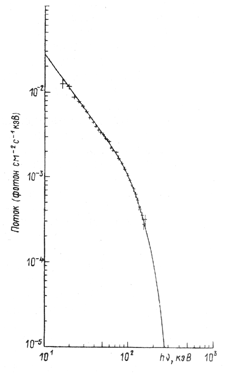
naiti i opticheskuyu tolshinu plazmy. Primer takoi ocenki daet kandidat v chernye
dyry Cyg X-1. Ego spektr, poluchennyi na vysotnom ballone gruppoi Tryumpera
(Syunyaev i Tryumper, 1979)
prekrasno opisyvaetsya formuloi (29) s parametrami
plazmy
), mozhno ocenit' znachenie temperatury, i ispol'zuya ee,
naiti i opticheskuyu tolshinu plazmy. Primer takoi ocenki daet kandidat v chernye
dyry Cyg X-1. Ego spektr, poluchennyi na vysotnom ballone gruppoi Tryumpera
(Syunyaev i Tryumper, 1979)
prekrasno opisyvaetsya formuloi (29) s parametrami
plazmy ![]() = 26.5 keV i
= 26.5 keV i ![]() =2 (ris. 10).
=2 (ris. 10).
Kogda plazma yavlyaetsya relyativistskoi, t.e.
![]() ,
uravnenie Kompaneica neprimenimo, i neohodimy raschety metodom Monte-Karlo
(Pozdnyakov, Sobol' i Syunyaev, 1982)
,
uravnenie Kompaneica neprimenimo, i neohodimy raschety metodom Monte-Karlo
(Pozdnyakov, Sobol' i Syunyaev, 1982)
Takie raschety pokazali, chto rasseyanie nizkochastotnyh fotonov v oblake
relyativistskoi plazmy s temperaturoi
![]() formiruet stepennoi spektr s pokazatelem
formiruet stepennoi spektr s pokazatelem ![]() , lineino zavisyashim ot
, lineino zavisyashim ot
![]() , logarifma opticheskoi tolshiny oblaka:
, logarifma opticheskoi tolshiny oblaka:
Ostroumnyi sposob analiticheskoi ocenki pokazatelya stepeni v spektre dlya takoi
zadachi byl predlozhen Ya.B. Zel'dovichem. Deistvitel'no, kak otmechalos' ranee,
pri kazhdom rasseyanii fotona na ul'trarelyativistskom elektrone s energiei
![]() chastota fotona vozrastaet v
chastota fotona vozrastaet v ![]() raz.
Predpolozhim, chto pri maksvellovskom raspredelenii elektronov po skorostyam
energiya fotona vozrastaet v srednem v
raz.
Predpolozhim, chto pri maksvellovskom raspredelenii elektronov po skorostyam
energiya fotona vozrastaet v srednem v
![]() raz. Posle
raz. Posle ![]() rasseyanii energiya vozrastaet v
rasseyanii energiya vozrastaet v
![]() raz, t.e.
raz, t.e.
![]() . S drugoi storony, v plazme maloi opticheskoi
tolshiny veroyatnost', chto foton ispytaet odno rasseyanie, ravna
. S drugoi storony, v plazme maloi opticheskoi
tolshiny veroyatnost', chto foton ispytaet odno rasseyanie, ravna
![]() , a
, a ![]() rasseyanii - po poryadku velichiny
rasseyanii - po poryadku velichiny ![]() . Yasno, chto
intensivnost' izlucheniya na chastote
. Yasno, chto
intensivnost' izlucheniya na chastote ![]() proporcional'na
proporcional'na ![]() rasseyaniyam:
rasseyaniyam:
| (32) |
<< 4. Kratkie harakteristiki istochnikov | Oglavlenie | 6. Vliyanie mezhzvezdnogo poglosheniya ... >>
|
Publikacii s klyuchevymi slovami:
rentgenovskoe izluchenie - kosmicheskie observatorii - detektory izlucheniya - rentgenovskie istochniki
Publikacii so slovami: rentgenovskoe izluchenie - kosmicheskie observatorii - detektory izlucheniya - rentgenovskie istochniki | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |