Astronet > Eshe raz o raduge

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Eshe raz o raduge

E. D. Trifonov (Rossiiskii gosudarstvennyi pedagogicheskii universitet im. A.I. Gercena, Sankt-Peterburg)
Opublikovano v Sorosovskom obrazovatel'nom zhurnale, N 7, 2000 g. Soderzhanie

Kak narisovat' radugu

Teper' my mozhem narisovat' shemu nablyudeniya radugi. Takoe postroenie vypolneno na ris. 5. Snachala risuem poverhnost' Zemli i stoyashego na nei nablyudatelya. Pered nablyudatelem nahoditsya zavesa dozhdya (zakrashennaya serym cvetom). Zatem izobrazhaem solnechnye luchi, napravlenie kotoryh zavisit ot vysoty Solnca nad gorizontom. Cherez glaz nablyudatelya provodim krasnye i fioletovye luchi pod ukazannymi vyshe uglami po otnosheniyu k solnechnym lucham. Mozhno byt' uverennym na osnovanii rezul'tatov predydushego razdela, chto eti luchi vozniknut v rezul'tate rasseyaniya na sootvetstvuyushih kaplyah dozhdya. Pri etom, kak sleduet iz ris. 2, nizhnyaya raduga obuslovlena processami rasseyaniya s odnim otrazheniem, a verhnyaya - s dvumya otrazheniyami. Obratite vnimanie na cheredovanie cvetov: fioletovye luchi yavlyayutsya vneshnimi, a krasnye - vnutrennimi. Ochevidno, chto luchi drugih cvetov v kazhdoi raduge razmeshayutsya mezhdu krasnym i fioletovym v sootvetstvii so znacheniyami pokazatelei prelomleniya.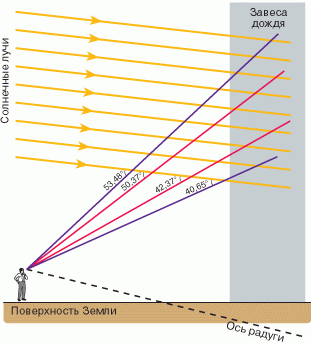

Ris. 5.Shema nablyudeniya radugi

Napomnim, chto my poka rassmatrivali izobrazhenie radugi v vertikal'noi ploskosti, prohodyashei cherez glaz nablyudatelya i polozhenie Solnca. Provedem pryamuyu, prohodyashuyu cherez glaz nablyudatelya parallel'no solnechnomu luchu. Esli vertikal'nuyu ploskost' povorachivat' vokrug ukazannoi pryamoi, to ee novoe polozhenie dlya nablyudeniya radugi budet sovershenno ekvivalentno ishodnomu. Poetomu raduga imeet formu dugi okruzhnosti, centr kotoroi nahoditsya na postroennoi osi. Radius etoi okruzhnosti (kak vidno na ris. 5) priblizitel'no raven rasstoyaniyu nablyudatelya do zavesy dozhdya.

Otmetim, chto pri nablyudenii radugi Solnce ne dolzhno stoyat' slishkom vysoko nad gorizontom - ne bolee chem na ${53,48}^\circ$ . Inache kartina luchei na risunke budet povorachivat'sya po chasovoi strelke, tak chto dazhe fioletovyi luch verhnei radugi ne smozhet popast' v glaz nablyudatelya, stoyashego na Zemle. Pravda, eto okazhetsya vozmozhnym, esli nablyudatel' podnimetsya na nekotoruyu vysotu, naprimer na samolete. Esli nablyudatel' podnimetsya dostatochno vysoko, to on smozhet uvidet' radugu i v forme polnoi okruzhnosti.

Dannoe opisanie radugi sleduet utochnit' c uchetom togo, chto solnechnye luchi ne strogo parallel'ny. Eto svyazano s tem, chto luchi, padayushie na kaplyu ot raznyh tochek Solnca, imeyut neskol'ko razlichnye napravleniya. Maksimal'noe uglovoe rashozhdenie luchei opredelyaetsya uglovym diametrom Solnca, kak izvestno ravnym priblizitel'no ${0,5}^\circ$ . K chemu eto privodit? Kazhdaya kaplya ispuskaet v glaz nablyudatelya ne stol' monohromaticheskii svet, kak eto bylo by v sluchae strogoi parallel'nosti padayushih luchei. Esli by uglovoi diametr Solnca zametno prevoshodil uglovoe rasstoyanie mezhdu fioletovym i krasnym luchami, to cveta radugi byli by nerazlichimy. K schast'yu, eto ne tak, hotya, nesomnenno, perekryvanie luchei s raznymi dlinami voln vliyaet na kontrastnost' cvetov radugi. Interesno, chto konechnost' uglovogo diametra Solnca byla uzhe uchtena v rabote Dekarta.

Popravka na difrakciyu

Privedennoe vyshe ob'yasnenie radugi bylo vypolneno na osnovanii geometricheskoi optiki. No izvestno, chto svet imeet volnovuyu prirodu i geometricheskaya optika yavlyaetsya lish' nekotorym priblizheniem. V etom razdele my rassmotrim, naskol'ko eto priblizhenie opravdanno v nashem sluchae.

Delo v tom, chto ponyatie o beskonechno uzkom puchke luchei yavlyaetsya abstrakciei. Esli svet padaet na krugloe otverstie diametra a, to iz-za volnovoi prirody (vspomnite princip Gyuigensa-Frenelya) proshedshii puchok sveta budet rasshiryat'sya i uglovoi razmer ego mozhet byt' oharakterizovan tak nazyvaemym difrakcionnym uglom $\lambda/a$ rad, gde $\lambda$ - dlina volny rassmatrivaemogo izlucheniya. V nashem sluchae svet otrazhaetsya ot kapli. Poetomu ocenka difrakcionnogo ushireniya, esli prinyat' diametr kapli ravnym 1 mm, a dlinu volny 5*10^-5 sm, budet 5*10^-4 rad, ili ${0,03}^\circ$ .

Etu ocenku legko bylo poluchit', no ona yavlyaetsya gruboi. Iz predydushego ob'yasneniya radugi sleduet, chto aktivnymi oblastyami poverhnosti kapli yavlyayutsya lish' te uchastki (men'shego razmera), kotorye sootvetstvuyut ekstremal'nym (minimal'nym ili maksimal'nym) znacheniyam ugla rasseyaniya $\varphi$ . Poetomu poluchennoe vyshe difrakcionnoe ushirenie yavlyaetsya neskol'ko zanizhennym. Vypolnim bolee tochnuyu ocenku difrakcionnogo ushireniya. Dlya etogo approksimiruem (to est' priblizhenno zamenim) krivuyu $\varphi(y)$ v okrestnosti ekstremal'noi tochki paraboloi:

$\varphi(y) \approx \varphi_{0} + f_{0}\cdot{(y - y_{0})}^{2}$ ,

(7)

gde $\varphi_{0}$ - ekstremal'noe znachenie ugla rasseyaniya, y₀ - znachenie pricel'nogo rasstoyaniya, pri kotorom dostigaetsya ekstremal'noe znachenie ugla $\varphi$ , f - podgonochnyi parametr. Iz (7) sleduet, chto

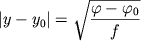$|y - y_{0}| = \sqrt{\displaystyle{\frac{\varphi - \varphi_{0}}{f}}}$ .

(8)

Zametim, chto interval | y - y₀ | harakterizuet intensivnost' padayushego na nego sveta i raven intervalu znachenii pricel'nogo parametra, iz kotorogo vyhodit svet (obratite vnimanie na simmetriyu hoda luchei na ris. 2), poetomu on opredelyaet i difrakcionnyi ugol. Opredelim interval ugla rasseyaniya $\varphi - \varphi_{0}$ , sootvetstvuyushii intervalu pricel'nogo parametra y - y₀ , tak, chtoby on byl raven difrakcionnomu uglu. To est' postavim uslovie

$\displaystyle{\frac{\lambda}{2R_{0}|y - y_{0}|}} = |\varphi - \varphi_{0}| = \Delta\varphi$ ,

gde R₀ - radius kapli (napomnim, chto pricel'nyi parametr y my vyrazhali v edinicah radiusa kapli).

Ispol'zuya (8), poluchaem

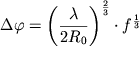$\Delta\varphi = {{\left(\displaystyle{\frac{\lambda}{2R_{0}}}\right)}^{\frac{2}{3}}}\cdot {f}^{\frac{1}{3}}$ .

(9)

Parametr f, kak my uzhe otmechali, mozhet byt' priblizhenno opredelen po grafikam na ris. 3. Te, kto znaet differencirovanie, mogut vyrazit' ego, kak eto sleduet iz (7), v vide

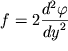
$f = 2\displaystyle{\frac{{d}^{2}\varphi}{{dy}^{2}}}$

v tochke ekstremuma. Pri etom, konechno, nado differencirovat' ne funkciyu, stoyashuyu v pravoi chasti uravneniya (7), a obshie vyrazheniya dlya ugla $\varphi$ , davaemye ishodnymi formulami (1) i (2). Vychisleniya privodyat k sleduyushim rezul'tatam: f = - 4,126 v pervom sluchae i f = 24,313 vo vtorom. Ispol'zuya eti dannye, mozhno po formule (9) vychislit' difrakcionnye ushireniya puchkov luchei v zavisimosti ot radiusa kapli. V tablice 1 my privodim rezul'taty etih vychislenii dlya krasnogo lucha ( $\lambda = 7*{10}^{-7}$ m) v obeih radugah.

Tablica 1

R, mm	$\Delta\varphi_{1}$		$\Delta\varphi_{2}$
R, mm	radiany	gradusy	radiany	gradusy
0,1	0,0370	2,11	0,0668	3,82
0,2	0,0232	1,33	0,0421	2,41
0,5	0,0126	0,72	0,0228	1,31
1,0	0,0079	0,45	0,0144	0,82

Vidno, chto pri radiuse kapli v 1 mm difrakcionnoe ushirenie poryadka poloviny gradusa dlya pervoi radugi i okolo odnogo gradusa dlya drugoi. Napomnim, chto uglovaya shirina pervoi radugi ${1,72}^\circ$ , a vtoroi ${3,11}^\circ$ . S umen'sheniem radiusa kapli proishodit difrakcionnoe ushirenie puchkov luchei raznyh cvetov i ih perekryvanie. Krasnyi cvet radugi uzhe ploho razlichim pri radiuse kapli v 0,1 mm. Kogda radius kapli dostigaet znacheniya 0,02 mm, to vse cveta polnost'yu perekryvayutsya i raduga stanovitsya beloi.

Otstupaya nemnogo v storonu ot nashei osnovnoi temy - radugi, my hoteli by sformulirovat' (vytekayushee iz predydushego) sleduyushee obshee polozhenie: esli na sfericheskoe odnorodnoe telo padaet puchok monohromaticheskogo sveta, to naibolee yarkaya chast' rasseyannogo sveta sosredotochena v konicheskom sloe, tolshina kotorogo ogranichena lish' difrakcionnymi popravkami. Poprobuite poschitat' sami, kakaya budet uglovaya tolshina takogo sloya, esli diametr shara, napolnennogo vodoi, raven 1 m.

Recenzent stat'i V.V. Mihailin

Nazad | Vpered

Publikacii s klyuchevymi slovami: raduga - optika - prelomlenie sveta - dispersiya sveta Publikacii so slovami: raduga - optika - prelomlenie sveta - dispersiya sveta
Sm. takzhe: Raduzhnoe derevo Polnaya krugovaya raduga nad Norvegiei Dopolnitel'nye radugi nad N'yu-Dzhersi Kogda radugi ulybayutsya Krasnaya oblachnaya raduga nad Delaverom Zakat, pohozhii na sloenyi pirog Raduga i luchi nad Brais-Kan'on Vse publikacii na tu zhe temu >>

Mneniya chitatelei [3]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce