Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

I. Vrashenie tverdogo tela vokrug nepodvizhnoi osi.

V etom sluchae dvizhenie tverdogo tela opredelyaetsya uravneniem

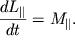${\displaystyle \frac{\displaystyle {\displaystyle dL_{\parallel} }}{\displaystyle {\displaystyle dt}}} = M_{\parallel} .$

Zdes' $L_{\parallel}$ - eto moment impul'sa otnositel'no osi vrasheniya, to est' proekciya na os' momenta impul'sa, opredelennogo otnositel'no nekotoroi tochki, prinadlezhashei osi (sm. lekciyu 2). $M_{\parallel}$ - eto moment vneshnih sil otnositel'no osi vrasheniya, to est' proekciya na os' rezul'tiruyushego momenta vneshnih sil, opredelennogo otnositel'no nekotoroi tochki, prinadlezhashei osi, prichem vybor etoi tochki na osi, kak i v sluchae s $L_{\parallel} ,$ znacheniya ne imeet. Deistvitel'no (ris. 3.4), $M_{\parallel} = rF\cos \alpha = \rho F,$ gde $F$ - sostavlyayushaya sily, prilozhennoi k tverdomu telu, perpendikulyarnaya osi vrasheniya, $\rho$ - plecho sily $F$ otnositel'no osi.

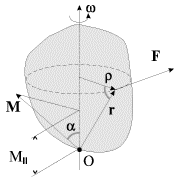Ris. 3.4.

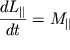Poskol'ku $L_{\parallel} = J\omega$ ( $J = \int {\displaystyle \rho ^{2}} dm$ - moment inercii tela otnositel'no osi vrasheniya), to vmesto $\frac{\displaystyle {\displaystyle dL_{\parallel} }}{\displaystyle {\displaystyle dt}}} = M_{\parallel$ mozhno zapisat'

$\frac{\displaystyle {\displaystyle d}}{\displaystyle {\displaystyle dt}}}\left( {\displaystyle J\omega} \right) = M_{\parallel$

(3.8)

ili

$J{\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}} = M_{\parallel} ,$

(3.9)

poskol'ku v sluchae tverdogo tela $J = {\displaystyle \rm const}.$

Uravnenie (3.9) i est' osnovnoe uravnenie dinamiki vrashatel'nogo dvizheniya tverdogo tela vokrug nepodvizhnoi osi. Ego vektornaya. forma imeet vid:

$J{\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf M}_{\parallel}$

(3.10)

Vektor $\omega$ vsegda napravlen vdol' osi vrasheniya, a $\bf M}_{\parallel$ - eto sostavlyayushaya vektora momenta sily vdol' osi.

V sluchae $M_{\parallel} = 0$ poluchaem $\omega = {\displaystyle \rm const},$ sootvetstvenno i moment impul'sa otnositel'no osi $L_{\parallel}$ sohranyaetsya. Pri etom sam vektor L, opredelennyi otnositel'no kakoi-libo tochki na osi vrasheniya, mozhet menyat'sya. Primer takogo dvizheniya pokazan na ris. 3.5.

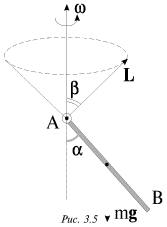Ris. 3.5.

Sterzhen' AV, sharnirno zakreplennyi v tochke A, vrashaetsya po inercii vokrug vertikal'noi osi takim obrazom, chto ugol $\alpha$ mezhdu os'yu i sterzhnem ostaetsya postoyannym. Vektor momenta impul'sa L, otnositel'no tochki A dvizhetsya po konicheskii poverhnosti s uglom polurastvora $\beta = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}} - \alpha$ odnako proekciya L na vertikal'nuyu os' ostaetsya postoyannoi, poskol'ku moment sily tyazhesti otnositel'no etoi osi raven nulyu.

Kineticheskaya energiya vrashayushegosya tela i rabota vneshnih sil (os' vrasheniya nepodvizhna).

Skorost' i -i chasticy tela

$v_{i} = \omega \rho _{i} ,$

(3.11)

gde $\rho _{i}$ - rasstoyanie chasticy do osi vrashenie Kineticheskaya energiya

$T = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \sum\limits_{i} {\displaystyle m_{i} } }v_{i}^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \sum\limits_{i} {\displaystyle m_{i} } }\rho _{i}^{2} \omega ^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}J\omega ^{2},$

(3.12)

tak kak uglovaya skorost' vrasheniya dlya vseh tochek odinakova.

V sootvetstvii s zakonom izmeneniya mehanicheskoi energii sistemy elementarnaya rabota vseh vneshnih sil ravna prirasheniyu kineticheskoi energii tela:

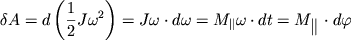$\delta A = d\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}J\omega ^{2}} \right) = J\omega \cdot d\omega = M_{\parallel} \omega \cdot dt = M_{{\displaystyle \left\| {\displaystyle } \right.}} \cdot d\varphi$

(3.13)

Rabota vneshnih sil pri povorote tela na konechnyi ugol $\varphi _{0}$ ravna

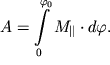$A = {\displaystyle \int\limits_{0}^{\varphi _{0} } {\displaystyle M_{\parallel} } } \cdot d\varphi .$

(3.14)

opustim, chto disk tochila vrashaetsya po inercii s uglovoe skorost'yu $\omega _{0} ,$ i my ostanavlivaem ego, prizhimaya kakoi-libo predmet k krayu diska s postoyannym usiliem. Pri etom na disk budet deistvovat' postoyannaya po velichine sila $F_{tr} ,$ napravlennaya perpendikulyarno ego osi. Rabota etoi sily

$A_{tr} = - F_{tr} \cdot R\varphi ,$

gde $R$ - radius diska, $\varphi$ - ugol ego povorota. Chislo oborotov, kotoroe sdelaet disk do polnoi ostanovki,

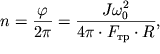$n = {\displaystyle \frac{\displaystyle {\displaystyle \varphi }}{\displaystyle {\displaystyle 2\pi }}} = {\displaystyle \frac{\displaystyle {\displaystyle J\omega _{0}^{2} }}{\displaystyle {\displaystyle 4\pi \cdot F_{tr} \cdot R}}},$

gde $J$ - moment inercii diska tochila vmeste s yakorem elektromotora.

Zamechanie. Esli sily takovy, chto $M_{\parallel} = 0,$ to rabotu oni ne proizvodyat.

Svobodnye osi. Ustoichivost' svobodnogo vrasheniya.

Pri vrashenii tela vokrug nepodvizhnoi osi eta os' uderzhivaetsya v neizmennom polozhenii podshipnikami. Pri vrashenii nesbalansirovannyh chastei mehanizmov osi (valy) ispytyvayut opredelennuyu dinamicheskuyu nagruzku, Voznikayut vibracii, tryaska, i mehanizmy mogut razrushit'sya.

Esli tverdoe telo raskrutit' vokrug proizvol'noi osi, zhestko svyazannoi s telom, i vysvobodit' os' iz podshipnikov, to ee napravlenie v prostranstve, voobshe govorya, budet menyat'sya. Dlya togo, chtoby proizvol'naya os' vrasheniya tela sohranyala svoe napravlenie neizmennym, k nei neobhodimo prilozhit' opredelennye sily. Voznikayushie pri etom situacii pokazany na ris. 3.6.

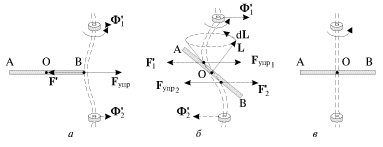Ris. 3.6.

V kachestve vrashayushegosya tela zdes' ispol'zovan massivnyi odnorodnyi sterzhen' AV, prikreplennyi k dostatochno elastichnoi osi (izobrazhena dvoinymi shtrihovymi liniyami). Elastichnost' osi pozvolyaet vizualizirovat' ispytyvaemye eyu dinamicheskie nagruzki. Vo vseh sluchayah os' vrasheniya vertikal'na, zhestko svyazana so sterzhnem i ukreplena v podshipnikah; sterzhen' raskruchen vokrug etoi osi i predostavlen sam sebe.

V sluchae, izobrazhennom na ris. 3.6a, os' vrasheniya yavlyaetsya dlya tochki V sterzhnya glavnoi, no ne central'noi, ${\displaystyle \bf L}\parallel \omega.$ Os' izgibaetsya, so storony osi na sterzhen' deistvuet sila ${\displaystyle \bf F}_{upr} ,$ obespechivayushaya ego vrashenie (v NISO, svyazannoi so sterzhnem, eta sila uravnoveshivaet centrobezhnuyu silu inercii). So storony sterzhnya na os' deistvuet sila ${\displaystyle {\displaystyle \bf F}}',$ uravnoveshennaya silami $\bf F'$ so storony podshipnikov.

V sluchae ris. 3.6b os' vrasheniya prohodit cherez centr mass sterzhnya i yavlyaetsya dlya nego central'noi, no ne glavnoi. Moment impul'sa otnositel'no centra mass O ne sohranyaetsya i opisyvaet konicheskuyu poverhnost'. Os' slozhnym obrazom deformiruetsya (izlamyvaetsya), so storony osi na sterzhen' deistvuyut sily $\bf F}_{upr.1$ i ${\displaystyle \bf F}_{upr.2},$ moment kotoryh obespechivaet prirashenie $d{\displaystyle \bf L}.$ (V NISO, svyazannoi so sterzhnem, moment uprugih sil kompensiruet moment centrobezhnyh sil inercii, deistvuyushih na odnu i druguyu poloviny sterzhnya). So storony sterzhnya na os' deistvuyut sily $\bf {\displaystyle F}'}_{1$ i ${\displaystyle \bf {\displaystyle F}'}_{2} ,$ napravlennye protivopolozhno silam $\bf F}_{upr.1$ i ${\displaystyle \bf F}_{upr.2}.$ Moment sil $\bf {\displaystyle F}'}_{1$ i ${\displaystyle \bf {\displaystyle F}'}_{2} ,$ uravnoveshen momentom sil $\bf F'}_{1$ i ${\displaystyle \bf F'}_{2} ,$ voznikayushih v podshipnikah.

I tol'ko v tom sluchae, kogda os' vrasheniya sovpadaet s glavnoi central'noi os'yu inercii tela (ris.3.6v), raskruchennyi i predostavlennyi sam sebe sterzhen' ne okazyvaet na podshipniki nikakogo vozdeistviya. Takie osi nazyvayut svobodnymi osyami, potomu chto, esli ubrat' podshipniki, oni budut sohranyat' svoe napravlenie v prostranstve neizmennym.

Inoe delo, budet li eto vrashenie ustoichivym po otnosheniyu k malym vozmusheniyam, vsegda imeyushim mesto v real'nyh usloviyah. Opyty pokazyvayut, chto vrashenie vokrug glavnyh central'nyh osei s naibol'shim i naimen'shim momentami inercii yavlyaetsya ustoichivym, a vrashenie vokrug osi s promezhutochnym znacheniem momenta inercii - neustoichivym. V etom mozhno ubedit'sya, podbrasyvaya vverh telo v vide parallelepipeda, raskruchennoe vokrug odnoi iz treh vzaimno perpendikulyarnyh glavnyh central'nyh osei (ris. 3.7). Os' AA' sootvetstvuet naibol'shemu, os' BB' - srednemu, a os' CC' - naimen'shemu momentu inercii parallelepipeda. Esli podbrosit' takoe telo, soobshiv emu bystroe vrashenie vokrug osi AA' ili vokrug osi CC', mozhno ubedit'sya v tom, chto eto vrashenie yavlyaetsya vpolne ustoichivym. Popytki zastavit' telo vrashat'sya vokrug osi BB' k uspehu ne privodyat - telo dvizhetsya slozhnym obrazom, kuvyrkayas' v polete.

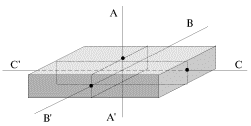Ris. 3.7.

V telah vrasheniya ustoichivoi okazyvaetsya svobodnaya os', sootvetstvuyushaya naibol'shemu momentu inercii. Tak, esli sploshnoi odnorodnyi disk podvesit' k bystrovrashayushemusya valu elektromotora (ris. 3.8, os' vrasheniya vertikal'na), to disk dovol'no bystro zaimet gorizontal'noe polozhenie, ustoichivo vrashayas' vokrug central'noi osi, perpendikulyarnoi k ploskosti diska.

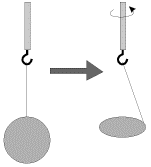Ris. 3.8.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce