Mehanika tverdogo tela. Lekcii.
V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie
Centr udara.
Opyt pokazyvaet, chto esli telo, zakreplennoe na osi vrasheniya, ispytyvaet udar, to deistvie udara v obshem sluchae peredaetsya i na os'. Pri etom velichina i napravlenie sily, prilozhennoi k osi, zavisyat ot togo, v kakuyu tochku tela nanesen udar.
Rassmotrim sploshnoi odnorodnyi sterzhen' AV, podveshennyi v tochke A na gorizontal'noi, zakreplennoi v podshipnikah osi OO' (ris. 3.9). Esli udar (korotkodeistvuyushaya sila F ( nanesen blizko k osi vrasheniya, to os' progibaetsya v napravlenii deistviya sily F (ris. 3.9a). Esli udar nanesen po nizhnemu koncu sterzhnya, vblizi tochki V, to os' progibaetsya v protivopolozhnom napravlenii (ris. 3.9b). Nakonec, esli udar nanesen v strogo opredelennuyu tochku sterzhnya, nazyvaemuyu centrom udara (ris. 3.9v, tochka S), to os' ne ispytyvaet nikakih dopolnitel'nyh nagruzok, svyazannyh s udarom. Ochevidno, v etom sluchae skorost' postupatel'nogo dvizheniya, priobretaemogo tochnoi A vmeste s centrom mass O, budet kompensirovat'sya lineinoi skorost'yu vrashatel'nogo dvizheniya vokrug centra mass O (oba eti dvizheniya iniciiruyutsya siloi F i proishodyat odnovremenno).
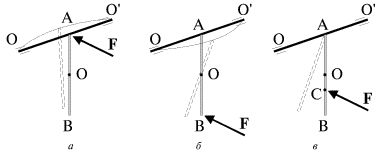 |
| Ris. 3.9. |
Vychislim, na kakom rasstoyanii ![]() ot tochki podvesa sterzhnya nahoditsya
centr udara. Uravnenie momentov otnositel'no osi vrasheniya OO' daet
ot tochki podvesa sterzhnya nahoditsya
centr udara. Uravnenie momentov otnositel'no osi vrasheniya OO' daet
| (3.15) |
Sil reakcii so storony osi, kak predpolagaetsya, pri udare ne voznikaet, poetomu na osnovanii teoremy o dvizhenii centra mass mozhno zapisat'
| (3.16) |
gde ![]() - massa tela,
- massa tela, ![]() - skorost' centra mass. Esli
- skorost' centra mass. Esli ![]() - rasstoyanie
ot osi do centra mass tela, to
- rasstoyanie
ot osi do centra mass tela, to
| (3.17) |
i v rezul'tate iz uravneniya momentov i uravneniya dvizheniya centra mass nahodim
| (3.18) |
Pri etom tochka C (centr udara) sovpadaet s tak nazyvaemym centrom kachaniya dannogo fizicheskogo mayatnika - tochkoi, gde nado sosredotochit' vsyu massu tverdogo tela, chtoby poluchennyi matematicheskii mayatnik imel takoi zhe period kolebanii, kak i dannyi fizicheskii.
V sluchae sploshnogo odnorodnogo sterzhnya dlinoi ![]() imeem:
imeem:
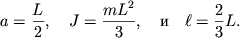 |
Zamechanie. Poluchennoe vyrazhenie dlya ![]() (3.18) spravedlivo i dlya
proizvol'nogo tverdogo tela. Pri etom nado tol'ko imet' v vidu, chto tochka
podvesa tela A i centr mass O dolzhny lezhat' na odnoi vertikali, a os'
vrasheniya dolzhna sovpadat' s odnoi iz glavnyh osei inercii tela, prohodyashih
cherez tochku A.
(3.18) spravedlivo i dlya
proizvol'nogo tverdogo tela. Pri etom nado tol'ko imet' v vidu, chto tochka
podvesa tela A i centr mass O dolzhny lezhat' na odnoi vertikali, a os'
vrasheniya dolzhna sovpadat' s odnoi iz glavnyh osei inercii tela, prohodyashih
cherez tochku A.
Primer 1. Pri udarah palkoi dlinoi ![]() po prepyatstviyu ruka "ne
chuvstvuet" udara (ne ispytyvaet otdachi) v tom sluchae, esli udar prihoditsya v
tochku, raspolozhennuyu na rasstoyanii
po prepyatstviyu ruka "ne
chuvstvuet" udara (ne ispytyvaet otdachi) v tom sluchae, esli udar prihoditsya v
tochku, raspolozhennuyu na rasstoyanii ![]() svobodnogo konca palki.
svobodnogo konca palki.
Primer 2. Pri gorizontal'nom udare kiem po bil'yardnomu sharu (ris. 3.10) shar nachinaet kachenie bez proskal'zyvaniya v tom sluchae, ecli udar nanesen v tochku, nahodyashuyusya na vysote
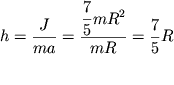 |
ot poverhnosti bil'yarda, to est' na ![]() vyshe centra
shara. Esli udar budet nanesen nizhe, kachenie budet soprovozhdat'sya skol'zheniem
v napravlenii dvizhenii shara. Esli udar nanesen vyshe, to shar v tochke kasaniya
s bil'yardnym stolom budet proskal'zyvat' nazad.
vyshe centra
shara. Esli udar budet nanesen nizhe, kachenie budet soprovozhdat'sya skol'zheniem
v napravlenii dvizhenii shara. Esli udar nanesen vyshe, to shar v tochke kasaniya
s bil'yardnym stolom budet proskal'zyvat' nazad.
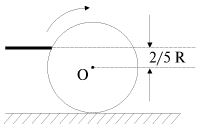 |
| Ris. 3.10. |
Rassmotrennye primery formal'no ne otnosyatsya k vrasheniyu tverdogo tela vokrug nepodvizhnoi osi, odnako vse privedennye vyshe soobrazheniya o centre udara, ochevidno, ostayutsya v sile i v etih sluchayah.
II. Ploskoe dvizhenie tverdogo tela.
Napomnim, chto pri ploskom dvizhenii vse tochki tela dvizhutsya v ploskostyah, parallel'nyh nekotoroi nepodvizhnoi ploskosti, poetomu dostatochno rassmotret' dvizhenie odnogo iz secheniya tela, naprimer, togo, v kotorom lezhit centr mass. Pri razlozhenii ploskogo dvizheniya na postupatel'noe i vrashatel'noe skorost' postupatel'nogo dvizheniya opredelena neodnoznachno - ona zavisit ot vybora osi vrasheniya, odnako uglovaya skorost' vrashatel'nogo dvizheniya okazyvaetsya odnoi i toi zhe (sm. lekciyu 1).
Esli v kachestve osi vrasheniya vybrat' os', prohodyashuyu cherez centr mass, to uravneniyami dvizheniya tverdogo tela budut:
1. Uravnenie dvizheniya centra mass
| (3.19) |
2. Uravnenie momentov otnositel'no osi, prohodyashei cherez centr mass
| (3.20) |
Osobennost'yu ploskogo dvizheniya yavlyaetsya to, chto os' vrasheniya sohranyaet svoyu orientaciyu v prostranstve i ostaetsya perpendikulyarnoi ploskosti, v kotoroi dvizhetsya centr mass. Eshe raz podcherknem, chto uravnenie momentov (3.20) zapisano otnositel'no, v obshem sluchae, uskorenno dvizhushegosya centra mass, odnako, kak bylo otmecheno v nachale lekcii, ono imeet takoi zhe vid, kak i uravnenie momentov otnositel'no nepodvizhnoi tochki.
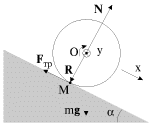
V kachestve primera rassmotrim zadachu o skatyvanii cilindra s naklonnoe ploskosti. Privedem dva sposoba resheniya etoi zadachi s ispol'zovaniem uravnenii dinamiki tverdogo tela.
Pervyi sposob. Rassmatrivaetsya vrashenie cilindra otnositel'no osi, prohodyashee cherez centr mass (ris. 3.11).
 |
| Ris. 3.11. |
Sistema uravnenii (3.19 - 3.20) imeet vid:
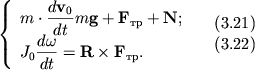 |
K etoi sisteme neobhodimo dobavit' uravnenie kinematicheskoi svyazi
| (3.23) |
Poslednee uravnenie poluchaetsya iz usloviya, chto cilindr skatyvaetsya bez proskal'zyvaniya, to est' skorost' tochki M cilindra ravna nulyu.
Uravnenie dvizheniya centra mass (3.1) zapishem dlya proekcii uskoreniya i sil na os' x vdol' naklonnoi ploskosti, a uravnenie momentov (3.22) - dlya proekcii uglovogo uskoreniya i momenta sily treniya na os' y , sovpadayushuyu s os'yu cilindra. Napravleniya osei x i u vybrany soglasovanno, v tom smysle, chto polozhitel'nomu lineinomu uskoreniyu osi cilindra sootvetstvuet polozhitel'noe zhe uglovoe uskorenie vrasheniya vokrug etoi osi. V itoge poluchim:
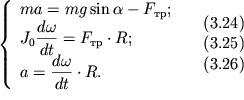 |
otkuda
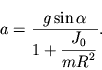 | (3.27) |
Sleduet podcherknut', chto ![]() - sila treniya scepleniya - mozhet
prinimat' lyuboe znachenie v intervale ot O do
- sila treniya scepleniya - mozhet
prinimat' lyuboe znachenie v intervale ot O do ![]() (sila treniya skol'zheniya) v zavisimosti ot
parametrov zadachi. Rabotu eta sila ne sovershaet, no obespechivaet uskorennoe
vrashenie cilindra pri ego skatyvanii s naklonnoi ploskosti. V dannom sluchae
(sila treniya skol'zheniya) v zavisimosti ot
parametrov zadachi. Rabotu eta sila ne sovershaet, no obespechivaet uskorennoe
vrashenie cilindra pri ego skatyvanii s naklonnoi ploskosti. V dannom sluchae
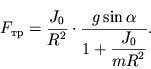 | (3.28) |
Esli cilindr sploshnoi, to
| (3.29) |
Kachenie bez proskal'zyvaniya opredelyaetsya usloviem
| (3.30) |
gde ![]() - koefficient treniya skol'zheniya,
- koefficient treniya skol'zheniya, ![]() - sila reakcii
opory. Eto uslovie svoditsya k sleduyushemu:
- sila reakcii
opory. Eto uslovie svoditsya k sleduyushemu:
| (3.31) |
ili
| (3.32) |
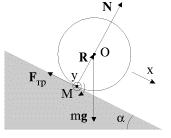
Vtoroi sposob. Rassmatrivaetsya vrashenie cilindra otnositel'no nepodvizhnoi osi, sovpadayushei v dannyi moment vremeni s mgnovennoi os'yu vrasheniya (ris. 3.12).
 |
| Ris. 3.12. |
Mgnovennaya os' vrasheniya prohodit cherez tochku soprikosnoveniya cilindra i ploskosti (tochku M). Pri takom podhode otpadaet neobhodimost' v uravnenii dvizhenii centra mass i uravnenii kinematicheskoi svyazi. Uravnenie momentov otnositel'no mgnovennoi osi imeet vid:
| (3.33) |
Zdes'
| (3.34) |
V proekcii na os' vrasheniya (os' y)
| (3.35) |
Uskorenie centra mass vyrazhaetsya cherez uglovoe uskorenie
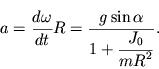 | (3.36) |
|
Publikacii s klyuchevymi slovami:
mehanika - tverdoe telo - ugly Eilera
Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera | |
|
Sm. takzhe:
| |