Mehanika tverdogo tela. Lekcii.
V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie
Kineticheskaya energiya pri ploskom dvizhenii.
Kineticheskaya energiya tverdogo tela predstavlyaet soboi summu kineticheskih energii otdel'nyh chastic:
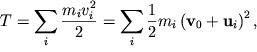 | (3.37) |
gde ![]() - skorost' centra mass tela,
- skorost' centra mass tela, ![]() - skorost'
i-i chasticy otnositel'no sistemy koordinat, svyazannoi s centrom mass i
sovershayushei postupatel'noe dvizhenie vmeste s nim. Vozvodya summu skorostei v
kvadrat, poluchim:
- skorost'
i-i chasticy otnositel'no sistemy koordinat, svyazannoi s centrom mass i
sovershayushei postupatel'noe dvizhenie vmeste s nim. Vozvodya summu skorostei v
kvadrat, poluchim:
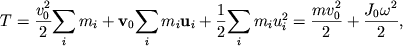 | (3.38) |
tak kak ![]() (summarnyi impul's
chastic v sisteme centra mass raven nulyu).
(summarnyi impul's
chastic v sisteme centra mass raven nulyu).
Takim obrazom, kineticheskaya energiya pri ploskom dvizhenii ravna summe kineticheskih energii postupatel'nogo i vrashatel'nogo dvizhenii (teorema Keniga). Esli rassmatrivat' ploskoe dvizhenie kak vrashenie vokrug mgnovennoi osi, to kineticheskaya energiya tela est' energiya vrashatel'nogo dvizheniya.
V etoi svyazi zadachu o skatyvanii cilindra s naklonnoi ploskosti mozhno reshit', ispol'zuya zakon sohraneniya mehanicheskoi energii (napomnim, chto sila treniya pri kachenii bez proskal'zyvaniya rabotu ne sovershaet).
Prirashenie kineticheskoi energii cilindra ravno ubyli ego potencial'noe energii:
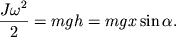 | (3.39) |
Zdes' ![]() - dlina naklonnoi ploskosti,
- dlina naklonnoi ploskosti, ![]() - moment
inercii cilindra otnositel'no mgnovennoi osi vrasheniya.
- moment
inercii cilindra otnositel'no mgnovennoi osi vrasheniya.
Poskol'ku skorost' osi cilindra ![]() to
to
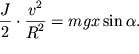 | (3.40) |
Differenciruya obe chasti etogo uravneniya po vremeni, poluchim
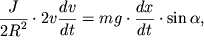 | (3.41) |
otkuda dlya lineinogo uskoreniya ![]() osi cilindra budem
imet' to zhe vyrazhenie, chto i pri chisto dinamicheskom sposobe resheniya (sm.
(3.27, 3.36)).
osi cilindra budem
imet' to zhe vyrazhenie, chto i pri chisto dinamicheskom sposobe resheniya (sm.
(3.27, 3.36)).
Zamechanie. Esli cilindr katitsya s proskal'zyvaniem, to izmenenie ego kineticheskoi energii budet opredelyat'sya takzhe i rabotoi sil treniya. Poslednyaya, v otlichie ot sluchaya, kogda telo skol'zit po sherohovatoi poverhnosti, ne vrashayas', opredelyaetsya, v sootvetstvii s (3.14), polnym uglom povorota cilindra, a ne rasstoyaniem, na kotoroe peremestilas' ego os'.
III. Dvizhenie aksial'no simmetrichnogo tverdogo tela, zakreplennogo v centre mass.
Takoe dvizhenie mozhno realizovat' s pomosh'yu special'nogo ustroistva, nazyvaemogo kardanovym podvesom (ris. 3.13). Polozhenie tela v podvese dolzhno byt' takim, chtoby osi AA', BB' i CC' peresekalis' v centre mass. V etom sluchae pri lyubyh vozmozhnyh dvizheniyah tela ego centr mass ostaetsya nepodvizhnym. Pri etom os' AA' (v dannom sluchae - os' simmetrii tela) mozhet zanimat' proizvol'nuyu orientaciyu v prostranstve.
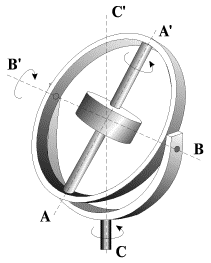 |
| Ris. 3.13. |
Zadachei o dvizhenii tverdogo tela, zakreplennogo v tochke, zanimalis' mnogie uchenye: L. Eiler, bol'shaya chast' zhizni kotorogo byla svyazana s Peterburgskoi Akademiei Nauk, vydayushiesya russkie uchenye N. E. .Zhukovskie, S. V. Kovalevskaya, S. A. Chaplygin, francuzskie uchenye Zh. Lagranzh, S. Puasson, L. Puanso. Okazalos', chto v obshem sluchae eta zadacha analiticheski nerazreshima. Dazhe v prosteishem sluchae dvizheniya tverdogo tela tol'ko pod deistviem sily tyazhesti tochnoe reshenie sushestvuet lish' v osobyh chastnyh sluchayah. Odin iz etih sluchaev, kogda odnorodnoe telo vrasheniya zakrepleno v centre mass, my rassmotrim v etoi lekcii, drugoi, imeyushii otnoshenie k dvizheniyu giroskopa, - v lekcii 4.
Uravneniya Eilera.
Rassmotrim odnorodnoe aksial'no simmetrichnoe telo vrasheniya, zakreplennoe v centre mass O (ris. 3.14). Central'nyi ellipsoid inercii takogo tela yavlyaetsya ellipsoidom vrasheniya s os'yu simmetrii Oz.
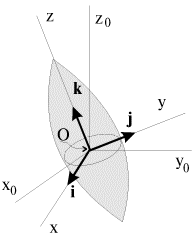 |
| Ris. 3.14. |
Sistema koordinat x0y0z0 na ris. 3.14 - laboratornaya,
sistema xyz zhestko svyazana s telom, prichem osi Ox, Oy i Oz - glavnye
central'nye osi inercii tela. Poskol'ku eto telo vrasheniya, to glavnye osevye
momenty inercii ![]() i
i ![]() ravny mezhdu soboi:
ravny mezhdu soboi: ![]()
Summarnyi moment sil tyazhesti otnositel'no tochki zakrepleniya (centra mass) raven nulyu, inyh sil, krome sil tyazhesti, net, poetomu uravnenie momentov (3.2) imeet vid
| (3.42) |
otkuda
| (3.43) |
to est' moment impul'sa raskruchennogo i predostavlennogo samomu sebe tela ostaetsya postoyannym po velichine i napravleniyu.
Zamechanie. Esli issleduemoe telo - shar, to ![]() i central'nyi ellipsoid inercii transformiruetsya v sferu. Eto oznachaet. chto
lyubaya central'naya os' vrasheniya yavlyaetsya glavnoi os'yu inercii shara, to est'
imeet mesto prostoe sootnoshenie
i central'nyi ellipsoid inercii transformiruetsya v sferu. Eto oznachaet. chto
lyubaya central'naya os' vrasheniya yavlyaetsya glavnoi os'yu inercii shara, to est'
imeet mesto prostoe sootnoshenie ![]() gde
gde ![]() - moment inercii
otnositel'no central'noi osi, i pri
- moment inercii
otnositel'no central'noi osi, i pri ![]() poluchaem
poluchaem ![]() Os' vrasheniya sovpadaet po napravleniyu s L i sohranyaet svoyu orientaciyu
v prostranstve.
Os' vrasheniya sovpadaet po napravleniyu s L i sohranyaet svoyu orientaciyu
v prostranstve.
Teper' dopustim, chto ![]() otlichno ot
otlichno ot ![]() i
i ![]() kak, naprimer,
na ris. 3.14. V etom sluchae chistoe vrashenie imeet mesto tol'ko togda, kogda
os' vrasheniya libo sovpadaet s os'yu simmetrii tela, libo perpendikulyarna k
nei.
kak, naprimer,
na ris. 3.14. V etom sluchae chistoe vrashenie imeet mesto tol'ko togda, kogda
os' vrasheniya libo sovpadaet s os'yu simmetrii tela, libo perpendikulyarna k
nei.
Obshii sluchai bolee slozhen; obychno ego rassmatrivayut s pomosh'yu differencial'nyh uravnenii Eilera. Delo zaklyuchaetsya v tom, chto esli v uravnenii (3.42) vektor L sproektirovat' na osi laboratornoi sistemy x0y0z0, to skalyarnye differencial'nye uravneniya dvizheniya budut ves'ma slozhnymi, poskol'ku momenty inercii otnositel'no nepodvizhnyh osei budut funkciyami vremeni. Poetomu gorazdo udobnee rassmatrivat' L, v proekciyah na osi sistemy xyz, zhestko svyazannoi s tverdym telom.
Pust' i, j, k - edinichnye orty sistemy xyz, zhestko svyazannoi s tverdym telom (ris. 3.14). Togda (3.42) prinimaet vid
| (3.44) |
gde ne tol'ko proekcii ![]() no i edinichnye orty i, j, k yavlyayutsya funkciyami vremeni. Poetomu iz (3.44) sleduet
no i edinichnye orty i, j, k yavlyayutsya funkciyami vremeni. Poetomu iz (3.44) sleduet
| (3.45) |
Zdes' ispol'zovan simvol ![]() chtoby podcherknut', chto rassmatrivayutsya izmeneniya vo vremeni proekcii
chtoby podcherknut', chto rassmatrivayutsya izmeneniya vo vremeni proekcii
![]() i
i ![]() otnositel'no podvizhnoi sistemy xyz - sistemy,
kotoraya, v svoyu ochered', povorachivaetsya vmeste s telom s mgnovennoi uglovoi
skorost'yu
otnositel'no podvizhnoi sistemy xyz - sistemy,
kotoraya, v svoyu ochered', povorachivaetsya vmeste s telom s mgnovennoi uglovoi
skorost'yu ![]()
Chto kasaetsya proizvodnyh po vremeni ot edinichnyh ortov i, j,
k , to ih izmeneniya vo vremeni obuslovleny tol'ko vrasheniem sistemy
xyz s uglovoi skorost'yu ![]() poetomu
poetomu
| (3.46) |
(sm. ris. 3.15). Podstavlyaya eti vyrazheniya v (3.45), poluchim:
| (3.47) |
Preobrazovanie
| (3.48) |
nahoditsya v polnoi analogii s preobrazovaniem skorosti pri perehode ot
nepodvizhnoi k vrashayusheisya sisteme koordinat. Sushestvenno, chto nablyudatel',
nahodyashiisya v sisteme xyz, fiksiruet tol'ko otnositel'noe izmenenie L
(chlen ![]() ).Dlya nablyudatelya v laboratornoi sisteme k otnositel'nomu izmeneniyu L
dobavlyaetsya ego "perenosnoe" izmenenie, svyazannoe s vrasheniem sistemy xyz s
mgnovennoi uglovoi skorost'yu
).Dlya nablyudatelya v laboratornoi sisteme k otnositel'nomu izmeneniyu L
dobavlyaetsya ego "perenosnoe" izmenenie, svyazannoe s vrasheniem sistemy xyz s
mgnovennoi uglovoi skorost'yu ![]()
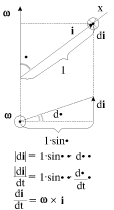 |
| Ris. 3.15. |
|
Publikacii s klyuchevymi slovami:
mehanika - tverdoe telo - ugly Eilera
Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera | |
|
Sm. takzhe:
| |