Mehanika tverdogo tela. Lekcii.
V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie
Proeciruya vektory L i ![]() na osi sistemy xyz, zhestko svyazannoi s
tverdym telom, poluchim:
na osi sistemy xyz, zhestko svyazannoi s
tverdym telom, poluchim:
| (3.49) |
| (3.50) |
| (3.51) |
Poskol'ku osi Ox, Oy i Oz - glavnye osi inercii dlya tochki zakrepleniya, to
![]() i iz (3.49-3.51) budem imet' sleduyushie uravneniya:
i iz (3.49-3.51) budem imet' sleduyushie uravneniya:
| (3.52) |
| (3.53) |
| (3.54) |
gde ![]() - glavnye momenty inercii tela. Obychno eti
uravneniya nazyvayut uravneniyami Eilera pri otsutstvii momentov vneshnih sil.
- glavnye momenty inercii tela. Obychno eti
uravneniya nazyvayut uravneniyami Eilera pri otsutstvii momentov vneshnih sil.
V chastnom sluchae (ris. 3.14) ![]() i iz (3.52-3.54) poluchaem:
i iz (3.52-3.54) poluchaem:
| (3.55) |
| (3.56) |
| (3.57) |
gde vvedeno oboznachenie
| (3.58) |
Iz (3.57) sleduet, chto ![]() to est' proekciya vektora
to est' proekciya vektora ![]() na os' simmetrii tela ostaetsya postoyannoi. Yasno, chto
na os' simmetrii tela ostaetsya postoyannoi. Yasno, chto ![]() - takzhe
postoyannaya velichina. Ee fizicheskii smysl stanovitsya ponyatnym, esli zapisat'
reshenie uravnenii (3.55, 3.56):
- takzhe
postoyannaya velichina. Ee fizicheskii smysl stanovitsya ponyatnym, esli zapisat'
reshenie uravnenii (3.55, 3.56):
| (3.59) |
gde ![]() -
proekciya vektora
-
proekciya vektora ![]() na ploskost' xy.
na ploskost' xy.
Takim obrazom, vektor ![]() sostavlyaet s os'yu simmetrii tela ugol
sostavlyaet s os'yu simmetrii tela ugol ![]() i vrashaetsya vokrug etoi
osi, kak sleduet iz (3.59), s postoyannoi uglovoi skorost'yu
i vrashaetsya vokrug etoi
osi, kak sleduet iz (3.59), s postoyannoi uglovoi skorost'yu ![]() Nachal'naya faza
Nachal'naya faza ![]() etogo vrasheniya opredelyaetsya nachal'nymi usloviyami.
etogo vrasheniya opredelyaetsya nachal'nymi usloviyami.
Posmotrim, kak budet vyglyadet' dvizhenie tverdogo tela v laboratornoi sisteme
x0y0z0. Poskol'ku nam izvestny znacheniya ![]() i
i ![]() to zakon dvizheniya tela (zavisimost' uglov
Eilera ot vremeni) v principe mozhet byt' poluchen iz kinematicheskih uravnenii
Eilera (1.30-1.32). Odnako eto svyazano s resheniem v obshem sluchae dovol'no
slozhnyh differencial'nyh uravnenii, poetomu my ogranichimsya kachestvennym
rassmotreniem dvizheniya tela. V silu togo, chto
to zakon dvizheniya tela (zavisimost' uglov
Eilera ot vremeni) v principe mozhet byt' poluchen iz kinematicheskih uravnenii
Eilera (1.30-1.32). Odnako eto svyazano s resheniem v obshem sluchae dovol'no
slozhnyh differencial'nyh uravnenii, poetomu my ogranichimsya kachestvennym
rassmotreniem dvizheniya tela. V silu togo, chto
| (3.60) |
(i, j, k - orty glavnyh osei inercii tela), a ![]() mozhno zapisat'
mozhno zapisat'
| (3.61) |
Zdes' dobavlen i vychten chlen ![]() chto pozvolyaet
predstavit' (3.61) v vide
chto pozvolyaet
predstavit' (3.61) v vide
| (3.62) |
Otsyuda vidno, chto k (os' figury), L i ![]() lezhat v odnoi
ploskosti. Iz (3.62) sleduet, chto
lezhat v odnoi
ploskosti. Iz (3.62) sleduet, chto
| (3.63) |
gde
| (3.64) |
est' sostavlyayushaya uglovoi skorosti po napravleniyu L. Ploskost', v
kotoroi lezhat os' figury, ![]() i L, povorachivaetsya (precessiruet)
vokrug napravleniya L s uglovoi skorost'yu
i L, povorachivaetsya (precessiruet)
vokrug napravleniya L s uglovoi skorost'yu ![]() nazyvaemoi skorost'yu
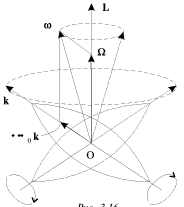
precessii (ris. 3.16). Samo dvizhenie nazyvaetsya regulyarnoi precessiei
svobodnogo simmetrichnogo volchka.
nazyvaemoi skorost'yu
precessii (ris. 3.16). Samo dvizhenie nazyvaetsya regulyarnoi precessiei
svobodnogo simmetrichnogo volchka.
 |
| Ris. 3.16. |
Otmetim, chto v sluchae veretenoobraznogo tela, izobrazhennogo na ris. 3.16,
![]() poetomu
poetomu ![]() (sm. (3.58)), i vektor -
(sm. (3.58)), i vektor -
![]() napravlen v tu zhe storonu, chto i k.
napravlen v tu zhe storonu, chto i k.
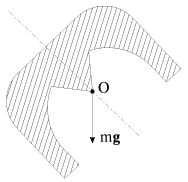
Zamechanie 1. Zakreplenie aksial'no simmetrichnogo tverdogo tela v centre mass mozhet byt' vypolneno ne tol'ko s pomosh'yu kardanova podvesa, no, naprimer, tak, kak pokazano na ris. 3.17. Massivnoe telo, sechenie kotorogo ploskost'yu risunka zashtrihovano, sharnirno zakrepleno v tochke O, sovpadayushei s centrom mass tela.
 |
| Ris. 3.17. |
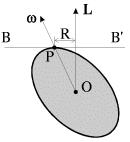
Zamechanie 2. Ispol'zuya postroenie Puanso (sm. lekciyu 2), regulyarnoi precessii svobodnogo simmetrichnogo volchka mozhno dat' naglyadnuyu geometricheskuyu interpretaciyu (ris. 3.18).
 |
| Ris. 3.18. |
Moment impul'sa L, tela otnositel'no nepodvizhnogo centra mass O
predstavlyaet soboi vektor, postoyannyi po velichine i napravleniyu. Ellipsoid
inercii tela s centrom v tochke O, sechenie kotorogo izobrazheno na ris. 3.18,
yavlyaetsya ellipsoidom vrasheniya. Kasatel'naya k ellipsoidu ploskost' BB'
provedena cherez polyus R peresecheniya mgnovennoi uglovoi skorosti ![]() s
ellipsoidom; eta ploskost' perpendikulyarna k vektoru L i v
laboratornoi sisteme otscheta sohranyaet svoe polozhenie neizmennym. Pri
regulyarnoi precessii volchka ellipsoid inercii tela katitsya po ploskosti
BB' bez skol'zheniya, tak chto geometricheskim mestom polyusov R yavlyaetsya
okruzhnost' radiusa
s
ellipsoidom; eta ploskost' perpendikulyarna k vektoru L i v
laboratornoi sisteme otscheta sohranyaet svoe polozhenie neizmennym. Pri
regulyarnoi precessii volchka ellipsoid inercii tela katitsya po ploskosti
BB' bez skol'zheniya, tak chto geometricheskim mestom polyusov R yavlyaetsya
okruzhnost' radiusa ![]() prinadlezhashaya ploskosti BB'.
prinadlezhashaya ploskosti BB'.
Zamechanie 3. Vo izbezhanie putanicy otmetim sleduyushee. Opisannoe vyshe
dvizhenie svyazano s izmeneniem ugla precessii ![]() (sm. ris. 1.3), poetomu
ono i bylo nazvano regulyarnoi precessiei (kinematicheskoe opredelenie).
Odnako sushestvuyut opredeleniya precescii kak dvizheniya osi simmetrii tela pod
deistviem momenta vneshnih sil (dinamicheskoe opredelenie, sm. lekciyu 4).
Opisannoe zhe vyshe dvizhenie s tochki zreniya dinamicheskogo opredeleniya nazyvayut
nutaciei.
(sm. ris. 1.3), poetomu
ono i bylo nazvano regulyarnoi precessiei (kinematicheskoe opredelenie).
Odnako sushestvuyut opredeleniya precescii kak dvizheniya osi simmetrii tela pod
deistviem momenta vneshnih sil (dinamicheskoe opredelenie, sm. lekciyu 4).
Opisannoe zhe vyshe dvizhenie s tochki zreniya dinamicheskogo opredeleniya nazyvayut
nutaciei.
|
Publikacii s klyuchevymi slovami:
mehanika - tverdoe telo - ugly Eilera
Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera | |
|
Sm. takzhe:
| |