Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Lekciya 4.

Giroskopy. Svobodnyi giroskop. Precessiya giroskopa pod deistviem vneshnih sil. Uglovaya skorost' precessii. Nutacii. Giroskopicheskie sily, ih priroda i proyavleniya.

Volchki. Ustoichivost' vrasheniya simmetrichnogo volchka.

Giroskop - eto massivnoe aksial'no-simmetrichnoe telo, vrashayusheesya s bol'shoi uglovoi skorost'yu vokrug svoei osi simmetrii.

V etom sluchae momenty vseh vneshnih sil, vklyuchaya i silu tyazhesti, otnositel'no centra mass giroskopa ravny nulyu. Eto mozhno realizovat', naprimer, pomestiv giroskop v kardanov podves, opisannyi v lekcii 3 i izobrazhennyi na ris. 3.13.

Pri etom

${\displaystyle \bf M}= 0;\quad {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}}}{\displaystyle {\displaystyle dt}}} = 0,$

(4.1)

i moment impul'sa sohranyaetsya:

${\displaystyle \bf L} = {\displaystyle \rm const}.$

(4.2)

Giroskop vedet sebya tak zhe, kak i svobodnee telo vrasheniya (sm. lekciyu 3). V zavisimosti ot nachal'nyh uslovii vozmozhny dva varianta povedeniya giroskopa:

1. Esli giroskop raskruchen vokrug osi simmetrii, to napravleniya momenta impul'sa i uglovoi skorosti sovpadayut:

${\displaystyle \bf L} = J\omega = {\displaystyle \rm const},$

(4.3)

i napravlenie osi simmetrii giroskopa ostaetsya neizmennym. V etom mozhno ubedit'sya, povorachivaya podstavku, na kotoroi raspolozhen kardanov podves - pri proizvol'nyh povorotah podstavki os' giroskopa sohranyaet neizmennoe napravlenie v prostranstve. Po etoi zhe prichine volchok, "zapushennyi" na liste kartona i podbroshennyi vverh (ris. 4.1), sohranyaet napravlenie svoei osi vo vremya poleta, i, padaya ostriem na karton, prodolzhaet ustoichivo vrashat'sya, poka ne izrashoduetsya zapas ego kineticheskoi energii.

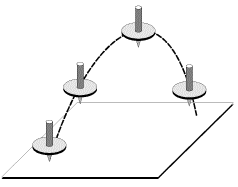Ris. 4.1.

Svobodnyi giroskop, raskruchennyi vokrug osi simmetrii, obladaet ves'ma znachitel'noi ustoichivost'yu. Iz osnovnogo uravneniya momentov sleduet, chto izmenenie momenta impul'sa

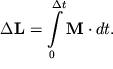$\Delta {\displaystyle \bf L} = {\displaystyle \int\limits_{0}^{\Delta t} {\displaystyle {\displaystyle \bf M}} } \cdot dt.$

(4.)

Esli interval vremeni $\Delta t$ mal, to i $\Delta {\displaystyle \bf L}$ malo, to est' pri kratkovremennyh vozdeistviyah dazhe ochen' bol'shih sil dvizhenie giroskopa izmenyaetsya neznachitel'no. Giroskop kak by soprotivlyaetsya popytkam izmenit' ego moment impul'sa i kazhetsya "zatverdevshim".

Voz'mem giroskop konusoobraznoi formy, opirayushiisya na sterzhen' podstavki v svoem centre mass O (ris. 4.2). Esli telo giroskopa ne vrashaetsya, to ono nahoditsya v sostoyanii bezrazlichnogo ravnovesiya, i maleishii tolchok sdvigaet ego s mesta.. Esli zhe eto telo privesti v bystroe vrashenie vokrug svoei osi, to dazhe sil'nye udary derevyannym molotkom ne smogut skol'ko-nibud' znachitel'no izmenit' napravlenie osi giroskopa v prostranstve. Ustoichivost' svobodnogo giroskopa ispol'zuetsya v razlichnyh tehnicheskih ustroistvah, naprimer, v avtopilote.

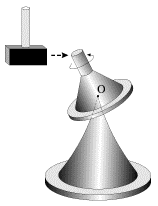Ris. 4.2.

2. Esli svobodnyi giroskop raskruchen tak, chto vektor mgnovennoi uglovoi skorosti i os' simmetrii giroskopa ne sovpadayut (kak pravilo, eto nesovpadenie pri bystrom vrashenii byvaet neznachitel'nym), to nablyudaetsya dvizhenie, opisannoe v lekcii 3 kak "svobodnaya regulyarnaya precessiya". Primenitel'no zhe k giroskopu ego nazyvayut nutaciei. Pri etom os' simmetrii giroskopa, vektory L i $\omega$ lezhat v odnoi ploskosti, kotoraya vrashaetsya vokrug napravleniya $\bf L}= {\displaystyle \rm const$ s uglovoi skorost'yu, ravnoi ${\displaystyle \frac{\displaystyle {\displaystyle L}}{\displaystyle {\displaystyle J_{x} }}},$ gde $J_{x}$ - moment inercii giroskopa otnositel'no glavnoi central'noi osi, perpendikulyarnoi osi simmetrii. Eta uglovaya skorost' (nazovem ee skorost'yu nutacii) pri bystrom sobstvennom vrashenii giroskopa okazyvaetsya dostatochno bol'shoi, i nutaciya vosprinimaetsya glazom kak melkoe drozhanie osi simmetrii giroskopa.

Nutacionnoe dvizhenie legko prodemonstrirovat' s pomosh'yu giroskopa, pokazannogo na ris. 4.2 - ono voznikaet pri udarah molotkom po sterzhnyu vrashayushegosya vokrug svoei osi giroskopa. Pri etom chem sil'nee raskruchen giroskop, tem bol'she ego moment impul'sa L - tem bol'she skorost' nutacii i tem "mel'che" drozhaniya osi figury. Etot opyt demonstriruet eshe odnu harakternuyu osobennost' nutacii - s techeniem vremeni ona postepenno umen'shaetsya i ischezaet. Eto - sledstvie neizbezhnogo treniya v opore giroskopa.

Nasha Zemlya - svoego roda giroskop, i ei tozhe svoistvenno nutacionnoe dvizhenie. Eto svyazano s tem, chto Zemlya neskol'ko priplyusnuta s polyusov, v silu chego momenty inercii otnositel'no osi simmetrii $\left( {\displaystyle J_{z} } \right)$ i otnositel'no osi, lezhashei v ekvatorial'noi ploskosti $\left( {\displaystyle J_{x} , J_{y} } \right)$ razlichayutsya. Pri etom $J_{x} = J_{y} ,$ a ${\displaystyle \frac{\displaystyle {\displaystyle J_{z} - J_{x} }}{\displaystyle {\displaystyle J_{x} }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 300}}}.$ V sisteme otscheta, svyazannoi s Zemlei, os' vrasheniya dvizhetsya po poverhnosti konusa vokrug osi simmetrii Zemli s uglovoi skorost'yu $\omega _{0} ,$ rasschityvaemoi po formule (3.58), to est' ona sovershaet odin oborot primerno za 300 dnei. Na samom dele v silu, kak predpolagaetsya, neabsolyutnoi zhestkosti Zemli, eto vremya okazyvaetsya bol'she - ono sostavlyaet okolo 440 sutok. Pri etom rasstoyanie tochki zemnoi poverhnosti, cherez kotoruyu prohodit os' vrashenii, ot tochki, cherez kotoruyu prohodit os' simmetrii (Severnyi polyus), ravno vsego neskol'kim metram. Nutacionnoe dvizhenie Zemli ne zatuhaet - po-vidimomu, ego podderzhivayut sezonnye izmeneniya, proishodyashie na poverhnosti

Precessiya giroskopa pod deistviem vneshnih sil. Elementarnaya teoriya.

Rassmotrim teper' situaciyu, kogda k osi giroskopa prilozhena sila, liniya deistviya kotoroi ne prohodit cherez tochku zakrepleniya. Opyty pokazyvayut, chto v etom sluchae giroskop vedet sebya ves'ma neobychnym obrazom.

Esli k osi sharnirno zakreplennogo v tochke O giroskopa (ris. 4.3) prikrepit' pruzhinu i tyanut' za nee vverh s siloi F , to os' giroskopa budet peremeshat'sya ne v napravlenii sily, a perpendikulyarno k nei, vbok. Eto dvizhenie nazyvaetsya precessiei giroskopa pod deistviem vneshnei sily.

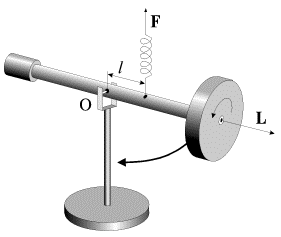Ris. 4.3.

Opytnym putem mozhno ustanovit', chto uglovaya skorost' precessii zavisit ne tol'ko ot velichiny sily $F$ (ris. 4.3), no i ot togo, k kakoi tochke osi giroskopa eta sila prilozhena: s uvelicheniem $F$ i ee plecha $\ell$ otnositel'no tochki zakrepleniya O skorost' precessii uvelichivaetsya. Pri etom okazyvaetsya, chto chem sil'nee raskruchen giroskop, tem men'she uglovaya skorost' precessii pri dannyh $F$ i $\ell .$

V kachestve sily F, vyzyvayushei precessiyu, mozhet vystupat' sila tyazhesti, esli tochka zakrepleniya giroskopa ne sovpadaet s centrom mass. Tak, esli sterzhen' s bystro vrashayushimsya diskom podvesit' na nitke (ris. 4.4), to on ne opuskaetsya vniz, kak eto mozhno bylo by predpolozhit', a sovershaet precessionnoe dvizhenie vokrug nitki. Nablyudenie precessii giroskopa pod deistviem sily tyazhesti v nekotorom smysle dazhe udobnee - liniya deistviya sily "avtomaticheski" smeshaetsya vmeste s os'yu giroskopa, sohranyaya svoyu orientaciyu v prostranstve.

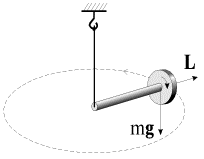Ris. 4.4.

Mozhno privesti i drugie primery precessii - naprimer, dvizhenie osi horosho izvestnoi detskoi igrushki - yuly s zaostrennym koncom (ris. 4.5). Yula, raskruchennaya vokrug svoei osi i postavlennaya na gorizontal'nuyu ploskost' slegka naklonno, nachinaet precessirovat' vokrug vertikal'noi osi pod deistviem sily tyazhesti (ris. 4.5).

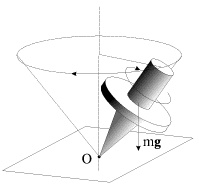Ris. 4.5.

Tochnoe reshenie zadachi o dvizhenii giroskopa v pole vneshnih sil dovol'no vyrazhenie dlya uglovoi skorosti precessii mozhno legko poluchit' v ramkah tak nazyvaemoi elementarnoi teorii giroskopa. V etoi teorii delaetsya dopushenie, chto mgnovennaya uglovaya skorost' vrasheniya giroskopa i ego moment impul'sa napravleny vdol' osi simmetrii giroskopa. Drugimi slovami, predpolagaetsya, chto uglovaya skorost' vrasheniya giroskopa vokrug svoei osi znachitel'no bol'she uglovoi skorosti precessii:

$\omega \gg \Omega ,$

(4.5)

tak chto vkladom v L, obuslovlennym precessionnym dvizheniem giroskopa, mozhno prenebrech'. V etom priblizhenii moment impul'sa giroskopa, ochevidno, raven

${\displaystyle \bf L} = J_{z} \omega,$

(4.6)

gde $J_{z}$ - moment inercii otnositel'no osi simmetrii.

Itak, rassmotrim tyazhelyi simmetrichnyi giroskop, u kotorogo nepodvizhnaya tochka S (tochka opory o podstavku) ne sovpadaet s centrom mass O (ris. 4.6).

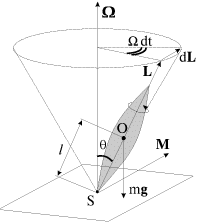Ris. 4.6.

Moment sily tyazhesti otnositel'no tochki S

$M = mg\ell \sin \theta ,$

(4.7)

gde $\theta$ - ugol mezhdu vertikal'yu i os'yu simmetrii giroskopa. Vektor M napravlen po normali k ploskosti, v kotoroi lezhat os' simmetrii giroskopa i vertikal', provedennaya cherez tochku S (ris. 4.6). Sila reakcii opory prohodit cherez S , i ee moment otnositel'no etoi tochki raven nulyu.

Izmenenie momenta impul'sa L opredelyaetsya vyrazheniem

$d{\displaystyle \bf L} = {\displaystyle \bf M} \cdot dt.$

(4.8)

Pri etom i L, i os' volchka precessiruyut vokrug vertikal'nogo napravleniya s uglovoi skorost'yu $\Omega.$ Eshe raz podcherknem: delaetsya dopushenie, chto vypolneno uslovie (4.5) i chto L postoyanno napravlen vdol' osi simmetrii giroskopa. Iz ris. 4.6 sleduet, chto

$dL = L \cdot \sin \theta \cdot \Omega \cdot dt.$

(4.9)

V vektornom vide

$d{\displaystyle \bf L} = \Omega\times {\displaystyle \bf L} \cdot dt.$

(4.10)

Sravnivaya (4.8) i (4.10), poluchaem sleduyushuyu svyaz' mezhdu momentom sily M, momentom impul'sa L i uglovoi skorost'yu precessii $\Omega$ :

${\displaystyle \bf M} = \Omega\times {\displaystyle \bf L}.$

(4.11)

Eto sootnoshenie pozvolyaet opredelit' napravlenie precessii pri zadannom napravlenii vrasheniya volchka vokrug svoei osi.

Obratim vnimanie, chto M opredelyaet uglovuyu skorost' precessii, a ne uglovoe uskorenie, poetomu mgnovennoe "vyklyuchenie" M privodit k mgnovennomu zhe ischeznoveniyu precessii, to est' precessionnoe dvizhenie yavlyaetsya bezynercionnym.

Sila, vyzyvayushaya precessionnoe dvizhenie, mozhet imet' lyubuyu prirodu. Dlya podderzhaniya etogo dvizheniya vazhno, chtoby vektor momenta sily M povorachivalsya vmeste s os'yu giroskopa. Kak uzhe bylo otmecheno, v sluchae sily tyazhesti eto dostigaetsya avtomaticheski. Pri etom iz (4.11) (sm. takzhe ris. 4.6) mozhno poluchit':

$mg\ell \cdot \sin \theta = \Omega J_{z} \omega \sin \theta .$

(4.12)

Esli uchest', chto v nashem priblizhenii spravedlivo sootnoshenie (4.6), to dlya uglovoi skorosti precessii poluchim

$\Omega = {\displaystyle \frac{\displaystyle {\displaystyle mg\ell }}{\displaystyle {\displaystyle J_{z} \omega }}}.$

(4.13)

Sleduet otmetit', chto $\Omega$ ne zavisit ot ugla $\theta$ naklona osi giroskopa i obratno proporcional'na $\omega ,$ chto horosho soglasuetsya s opytnymi dannymi.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce