Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Precessiya giroskopa pol deistviem vneshnih sil. Othod ot elementarnoi teorii. Nutacii.

Opyt pokazyvaet, chto precessionnoe dvizhenie giroskopa pod deistviem vneshnih sil v obshem sluchae slozhnee, chem to, kotoroe bylo opisano vyshe v ramkah elementarnoi teorii. Esli soobshit' giroskopu tolchok, izmenyayushii ugol $\theta$ (sm. ris. 4.6), to precessiya perestanet byt' ravnomernoi (chasto govoryat: regulyarnoi), a budet soprovozhdat'sya melkimi vrasheniyami i drozhaniyami vershiny giroskopa - nutaciyami. Dlya ih opisaniya neobhodimo uchest' nesovpadenie vektora polnogo momenta impul'sa L, mgnovennoi uglovoi skorosti vrasheniya $\omega$ i osi simmetrii giroskopa.

Tochnaya teoriya giroskopa vyhodit za ramki kursa obshei fiziki. Iz sootnosheniya $d{\displaystyle \bf L} = {\displaystyle \bf M}dt$ sleduet, chto konec vektora L dvizhetsya v napravlenii M, to est' perpendikulyarno k vertikali i k osi giroskopa. Eto znachit, chto proekcii vektora L na vertikal' $L_{B}$ i na os' giroskopa $L_{0}$ ostayutsya postoyannymi. Eshe odnoi postoyannoi yavlyaetsya energiya

$E = T + mg\ell \cdot \cos \theta ,$

(4.14)

gde $T$ - kineticheskaya energiya giroskopa. Vyrazhaya $L_{B}, L_{0}$ i $T$ cherez ugly Eilera i ih proizvodnye, mozhno, s pomosh'yu uravnenii Eilera, opisat' dvizhenie tela analiticheski.

Rezul'tat takogo opisaniya okazyvaetsya sleduyushim: vektor momenta impul'sa L opisyvaet nepodvizhnyi v prostranstve konus precessii, i pri etom os' simmetrii giroskopa dvizhetsya vokrug vektora L po poverhnosti konusa nutacii. Vershina konusa nutacii, kak i vershina konusa precessii, nahoditsya v tochke zakrepleniya giroskopa, a os' konusa nutacii sovpadaet po napravleniyu s L i dvizhetsya vmeste s nim. Uglovaya skorost' nutacii opredelyaetsya vyrazheniem

$\omega _{nut} = {\displaystyle \frac{\displaystyle {\displaystyle L}}{\displaystyle {\displaystyle J_{s} }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle J_{z} \omega }}{\displaystyle {\displaystyle J_{s} }}},$

(4.15)

gde $J_{z}$ i $J_{s}$ - momenty inercii tela giroskopa otnositel'no osi simmetrii i otnositel'no osi, prohodyashei cherez tochku opory i perpendikulyarnoi osi simmetrii, $\omega$ - uglovaya skorost' vrasheniya vokrug osi simmetrii (sravn. s (3.64)).

Takim obrazom, os' giroskopa uchastvuet v dvuh dvizheniyah: nutacionnom i precessionnom. Traektorii absolyutnogo dvizheniya vershiny giroskopa predstavlyayut soboi zamyslovatye linii, primery kotoryh predstavleny na ris. 4.7.

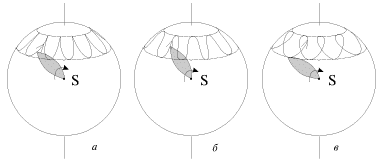Ris. 4.7.

Harakter traektorii, po kotoroi dvizhetsya vershina giroskopa, zavisit ot nachal'nyh uslovii. V sluchae ris. 4.7a giroskop byl raskruchen vokrug osi simmetrii, ustanovlen na podstavke pod nekotorym uglom k vertikali i ostorozhno otpushen. V sluchae ris. 4.7b emu, krome togo, byl soobshen nekotoryi tolchok vpered, a v sluchae ris. 4.7v - tolchok nazad po hodu precessii. Krivye na ris. 4.7 vpolne analogichny cikloidam, opisyvaemym tochkoi na obode kolesa, katyashegosya po ploskosti bez proskal'zyvaniya ili s proskal'zyvaniem v tu ili inuyu storonu. I lish' soobshiv giroskopu nachal'nyi tolchok vpolne opredelennoi velichiny i napravleniya, mozhno dobit'sya togo, chto os' giroskopa budet precessirovat' bez nutacii. Chem bystree vrashaetsya giroskop, tem bol'she uglovaya skorost' nutacii i tem men'she ih amplituda. Pri ochen' bystrom vrashenii nutacii delayutsya prakticheski nezametnymi dlya glaza.

Mozhet pokazat'sya strannym: pochemu giroskop, buduchi raskruchen, ustanovlen pod uglom k vertikali i otpushen, ne padaet pod deistviem sily tyazhesti, a dvizhetsya vbok? Otkuda beretsya kineticheskaya energiya precessionnogo dvizheniya?

Otvety na eti voprosy mozhno poluchit' tol'ko v ramkah tochnoi teorii giroskopam. Na samom dele giroskop deistvitel'no nachinaet padat', a precessionnoe dvizhenie poyavlyaetsya kak sledstvie zakona sohraneniya momenta impul'sa. V samom dele, otklonenie osi giroskopa vniz privodit k umen'sheniyu proekcii momenta impul'sa na vertikal'noe napravlenie. Eto umen'shenie dolzhno byt' skompensirovano momentom impul'sa, svyazannym s precessionnym dvizheniem osi giroskopa. S energeticheskoe tochki zreniya kineticheskaya energiya precessii poyavlyaetsya za schet izmeneniya potencial'noi energii giroskopam

Esli za schet treniya v opore nutacii gasyatsya bystree, chem vrashenie giroskopa vokrug osi simmetrii (kak pravilo, tak i byvaet), to vskore posle "zapuska" giroskopa nutacii ischezayut i ostaetsya chistaya precessiya (ris. 4.8). Pri etom ugol naklona osi giroskopa k vertikali $\left( {\displaystyle \theta _{2} } \right)$ okazyvaetsya bol'she, chem on byl vnachale $\left( {\displaystyle \theta _{1} } \right),$ to est' potencial'naya energiya giroskopa umen'shaetsya. Takim obrazom, os' giroskopa dolzhna nemnogo opustit'sya, chtoby imet' vozmozhnost' precessirovat' vokrug vertikal'noi osi.

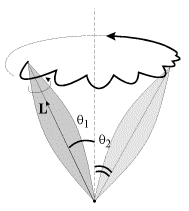Ris. 4.8.

Giroskopicheskie sily.

Obratimsya k prostomu opytu: voz'mem v ruki val AV s nasazhennym na nego kolesom S (ris. 4.9). Poka koleso ne raskrucheno, ne predstavlyaet nikakogo truda povorachivat' val v prostranstve proizvol'nym obrazom. No esli koleso raskrucheno, to popytki povernut' val, naprimer, v gorizontal'noi ploskosti s nebol'shoi uglovoi skorost'yu $\Omega$ privodyat k interesnomu effektu: val stremitsya vyrvat'sya iz ruk i povernut'sya v vertikal'noi ploskosti; on deistvuet na kisti ruk s opredelennymi silami $\bf R}_{A$ i $\bf R}_{B$ (ris. 4.9). Trebuetsya prilozhit' oshutimoe fizicheskoe usilie, chtoby uderzhat' val s vrashayushimsya kolesom v gorizontal'noi ploskosti.

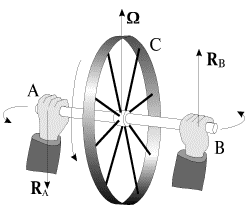Ris. 4.9.

Rassmotrim effekty, voznikayushie pri vynuzhdennom vrashenii osi giroskopa, bolee podrobno. Pust' os' giroskopa budet ukreplena v U-obraznoi rame, kotoraya mozhet povorachivat'sya vokrug vertikal'noi osi OO' (ris. 4.10). Takoi giroskop obychno nazyvayut nesvobodnym - ego os' lezhit v gorizontal'noi ploskosti i vyiti iz nee ne mozhet.

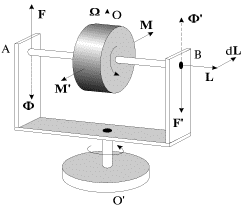Ris. 4.10.

Raskrutim giroskop vokrug ego vokrug ego osi simmetrii do bol'shoi uglovoi skorosti (moment impul'sa L) i stanem povorachivat' ramu s ukreplennym v nei giroskopom vokrug vertikal'noi osi OO' s nekotoroi uglovoi skorost'yu $\Omega,$ kak pokazano na ris. 4.10. Moment impul'sa L, poluchit pri etom prirashenie $d{\displaystyle \bf L},$ kotoroe dolzhno byt' obespecheno momentom sil M, prilozhennym k osi giroskopa. Moment M, v svoyu ochered', sozdan paroi sil ${\displaystyle \bf F}\div {\displaystyle \bf {\displaystyle F}'},$ voznikayushih pri vynuzhdennom povorote osi giroskopa i deistvuyushih na os' so storony ramy. Po tret'emu zakonu N'yutona os' deistvuet na ramu s silami $\bf F}\div {\displaystyle \bf F'$ (ris. 4.10). Eti sily nazyvayutsya giroskopicheskimi; oni sozdayut giroskopicheskii moment ${\displaystyle \bf {\displaystyle M}'}.$ Poyavlenie giroskopicheskih sil nazyvayut giroskopicheskim effektom. Imenno eti giroskopicheskie sily my i chuvstvuem, pytayas' povernut' os' vrashayushegosya kolesa (ris. 4.9).

Giroskopicheskii moment netrudno rasschitat'. Polozhim, soglasno elementarnoi teorii, chto

${\displaystyle \bf L} = J\omega$

(4.16)

gde $J$ - moment inercii giroskopa otnositel'no ego osi simmetrii, a $\omega$ - uglovaya skorost' sobstvennogo vrasheniya. Togda moment vneshnih sil, deistvuyushih na os', budet raven

${\displaystyle \bf M} = \Omega\times {\displaystyle \bf L} = \Omega\times \left( {\displaystyle J \omega} \right),$

(4.17)

gde $\omega$ - uglovaya skorost' vynuzhdennogo povorota (inogda govoryat: vynuzhdennoi precessii). So storony osi na podshipniki deistvuet protivopolozhnyi moment

${\displaystyle {\displaystyle \bf M}}' = - {\displaystyle \bf M} = J \omega\times \Omega$

(4.)

Takim obrazom, val giroskopa, izobrazhennogo na ris. 4.10, budet prizhimat'sya kverhu v podshipnike V i okazyvat' davlenie na nizhnyuyu chast' podshipnika A.

Napravlenie giroskopicheskih sil mozhno legko naiti s pomosh'yu pravila, sformulirovannogo N.E. Zhukovskim: giroskopicheskie sily stremyatsya sovmestit' moment impul'sa L giroskopa s napravleniem uglovoi skorosti vynuzhdennogo povorota. Eto pravilo mozhno naglyadno prodemonstrirovat' s pomosh'yu ustroistva, predstavlennogo na ris. 4.11.

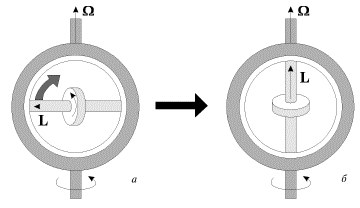Ris. 4.11.

Os' giroskopa zakreplena v kol'ce, kotoroe mozhet svobodno povorachivat'sya v oboime. Privedem oboimu vo vrashenie vokrug vertikal'noi osi s uglovoi skorost'yu $\Omega$ (vynuzhdennyi povorot), i kol'co s giroskopom budet povorachivat'sya v oboime do teh por, poka napravleniya L i $\Omega$ ne sovpadut. Takoi effekt lezhit v osnove izvestnogo magnitomehanicheskogo yavleniya - namagnichivaniya zheleznogo sterzhnya pri ego vrashenii vokrug sobstvennoi osi - pri etom spiny elektronov vystraivayutsya vdol' osi sterzhnya (opyt Barnetta).

Giroskopicheskie usiliya ispytyvayut podshipniki osei bystro vrashayushihsya chastei mashiny pri povorote samoi mashiny (turbiny na korable, vinta na samolete i t.d.). Pri znachitel'nyh velichinah uglovoi skorosti vynuzhdennoi precessii $\Omega$ i sobstvennogo vrasheniya $\omega ,$ a takzhe bol'shih razmerah mahovika eti sily mogut dazhe razrushit' podshipniki. Rassmotrim nekotorye primery proyavleniya giroskopicheskih sil.

Primer 1. Legkii odnomotornyi samolet s pravym vintom sovershaet levyi virazh (ris. 4.12). Giroskopicheskii moment peredaetsya cherez podshipniki A i V na korpus samoleta i deistvuet na nego, stremyas' sovmestit' os' sobstvennogo vrasheniya vinta (vektor $\omega$ ) s os'yu vynuzhdennoi precessii (vektor $\Omega$ ). Samolet nachinaet zadirat' nos kverhu, i letchik dolzhen "dat' ruchku ot sebya", to est' opustit' vniz rul' vysoty. Takim obrazom, moment giroskopicheskih sil budet kompensirovan momentom aerodinamicheskih sil.

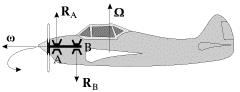Ris. 4.12.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce